
振动方程中参数的物理意义 A的物理意义: =xmx A是物体离开平衡位置的最大幅度一-振幅,A的大 小由弹簧振子的初始状态决定。单位 xo-Acoso vo=-@Asin o o的物理意义,分三步分析 (1)T的引入t=0x0=4cos Po 2π 0 x=Acos(@ 2元+0,)=Ac0s0=
振动方程中参数的物理意义 A 的物理意义: max A = x 0 x0 Acos0 t = = 0 0 0 ) cos 2 cos( 2 t = x = A + = A = x 0 0 0 0 sin cos v A x A = − = 2 0 2 0 ( ) v A = x + ω的物理意义,分三步分析 (1)T 的引入 A 是物体离开平衡位置的最大幅度-----振幅,A 的大 小由弹簧振子的初始状态决定。单位 m

T- 2灭 T表示完成一次完整振动所需要的时 ) 间-一一一周期,T的大小由弹簧振子的固有性质决定。单位 (2)v的引入)= 。表示在单位时间内完成整振动的次数一一一频率, 山的大小由弹簧振子的固有性质决定。单位z (3 的引入 .T- 2兀 ∴.0=2πV ) 。表示在2π秒内完成整振动的次数 角频率(圆频率)。 o的大小由弹簧振子的固有性质决定。单位弧度/秒
T 表示完成一次完整振动所需要的时 间-----周期,T 的大小由弹簧振子的固有性质决定。单位 2 T = T 1 = = 2 1 2 T = = (2) υ的引入 υ表示在单位时间内完成整振动的次数------频率, υ 的大小由弹簧振子的固有性质决定。单位Hz (3) ω的引入 ω表示在2π 秒内完成整振动的次数-------角频率(圆频率), ω的大小由弹簧振子的固有性质决定。单位弧度/秒

m 固有角频率 0=2πv→v 固有频率 m -71=2 固有周期
m k m k = = 2 m k 2 1 = 2 = k m T T 2 1 = = 固有角频率 固有频率 固有周期

·Po的物理意义: 我们称p=01+P为位相。则Po表示初始时刻的位相 一初 位相,9o的大小由弹簧振子的初始状态决定。单位rad.po取 值范围0≤p≤π 求P0方法: ①已知 x0,V0,0 xo-Acos po vo --@Asin po →tan o--yo x⊙
◼ 的物理意义: 我们称 为位相。则 表示初始时刻的位相-----初 位相, 的大小由弹簧振子的初始状态决定。单位rad. 取 值范围 求 方法: ①已知 0 0 x0 ,v0 , = − = 0 0 0 0 sin cos v A x A 0 0 0 tan x v = − = +0 t 0 0 0 0 0
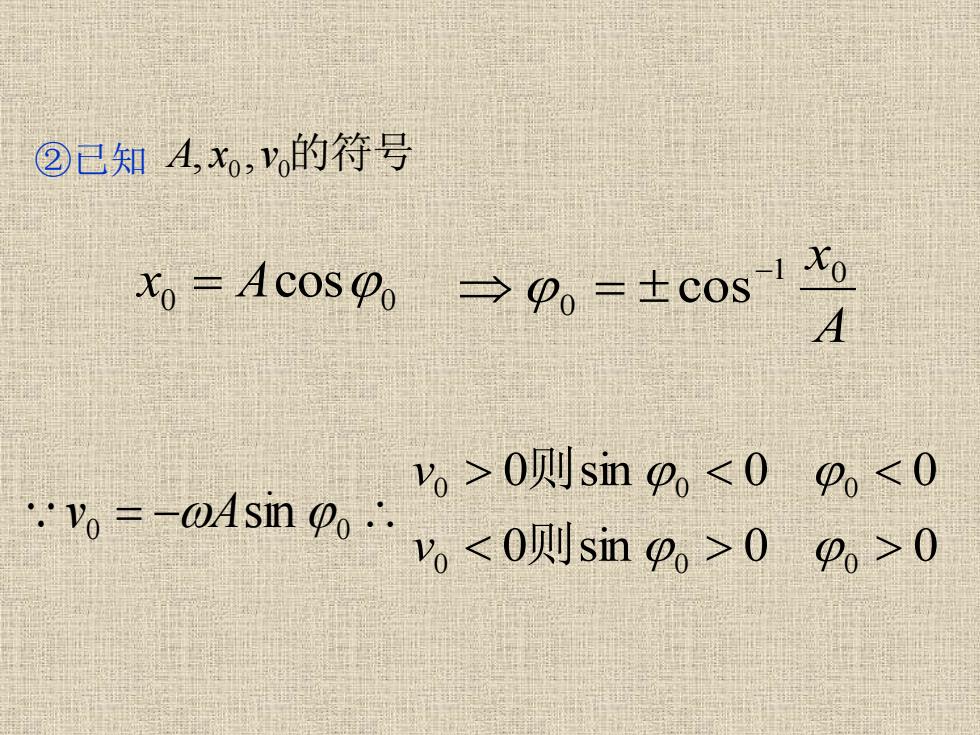
②已知A,x,的符号 Xo-AcosPo →P=±cos1 A ,>0则sinp<0p<0 =-01sn0%<0则sn0>0p>0
②已知 A, x0 ,v0 的符号 0 0 x = Acos A x 1 0 0 cos− = v0 = −Asin 0 0 sin 0 0 0 sin 0 0 0 0 0 0 0 0 则 则 v v