
碰撞理论的优点: 碰撞理论为我们描述了一幅虽然粗糙但十分明确 的反应图像,在反应速率理论的发展中起了很大作用 对Arrhenius公式中的指数项、指前因子和阈能 都提出了较明确的物理意义,认为指数项相当于有 效碰撞分数,指前因子A相当于碰撞频率。 它解释了一部分实验事实,理论所计算的速率常 数k值与较简单的反应的实验值相符。 缺点: 模型过于简单,所以要引入概率因子,且概率 因子的值很难具体计算。 阈能还必须从实验活化能求得,所以碰撞理论 还是半经验的
碰撞理论的优点: 模型过于简单,所以要引入概率因子,且概率 因子的值很难具体计算。 对Arrhenius公式中的指数项、指前因子和阈能 都提出了较明确的物理意义,认为指数项相当于有 效碰撞分数,指前因子A 相当于碰撞频率。 它解释了一部分实验事实,理论所计算的速率常 数 k 值与较简单的反应的实验值相符。 碰撞理论为我们描述了一幅虽然粗糙但十分明确 的反应图像,在反应速率理论的发展中起了很大作用 缺点: 阈能还必须从实验活化能求得,所以碰撞理论 还是半经验的

§12.2 过渡态理论 势能面 由过渡态理论计算反应速率常数 *活化络合物的活化能E,和指前因子A与 诸热力学函数之间的关系
§12.2 过渡态理论 势能面 由过渡态理论计算反应速率常数 *活化络合物的活化能Ea和指前因子A与 诸热力学函数之间的关系

过渡态理论(transition state theory) 过渡态理论是1935年由Eyring,Evans和 Polany等人在统计热力学和量子力学的基础上 提出来的。 他们认为由反应物分子变成生成物分子,中 间一定要经过一个过渡态,而形成这个过渡态必 须吸取一定的活化能,这个过渡态就称为活化络 合物,所以又称为活化络合物理论。 用该理论,只要知道分子的振动频率、质量、 核间距等基本物性,就能计算反应的速率常数,所 以又称为绝对反应速率理论
过渡态理论(transition state theory) 过渡态理论是1935年由Eyring,Evans和 Polany 等人在统计热力学和量子力学的基础上 提出来的。 他们认为由反应物分子变成生成物分子,中 间一定要经过一个过渡态,而形成这个过渡态必 须吸取一定的活化能,这个过渡态就称为活化络 合物,所以又称为活化络合物理论。 用该理论,只要知道分子的振动频率、质量、 核间距等基本物性,就能计算反应的速率常数,所 以又称为绝对反应速率理论

势能面 该理论认为反应物分子间相互作用的势能是 分子间相对位置的函数 E。=E,(r) 莫尔斯Morse)公式是对双原子分子最常用的 计算势能E的经验公式: E,(r)=D.[exp{-2a(r-)}-2exp{-a(r-)}] 式中r是分子中双原子分子间的平衡核间距, D,是势能曲线的井深,a为与分子结构有关的常数
势能面 莫尔斯(Morse)公式是对双原子分子最常用的 计算势能Ep的经验公式: p e 0 0 E r D a r r a r r ( ) [exp{ 2 ( )} 2exp{ ( )}] = − − − − − 式中r0是分子中双原子分子间的平衡核间距, De是势能曲线的井深,a为与分子结构有关的常数 该理论认为反应物分子间相互作用的势能是 分子间相对位置的函数 E E r p p = ( )
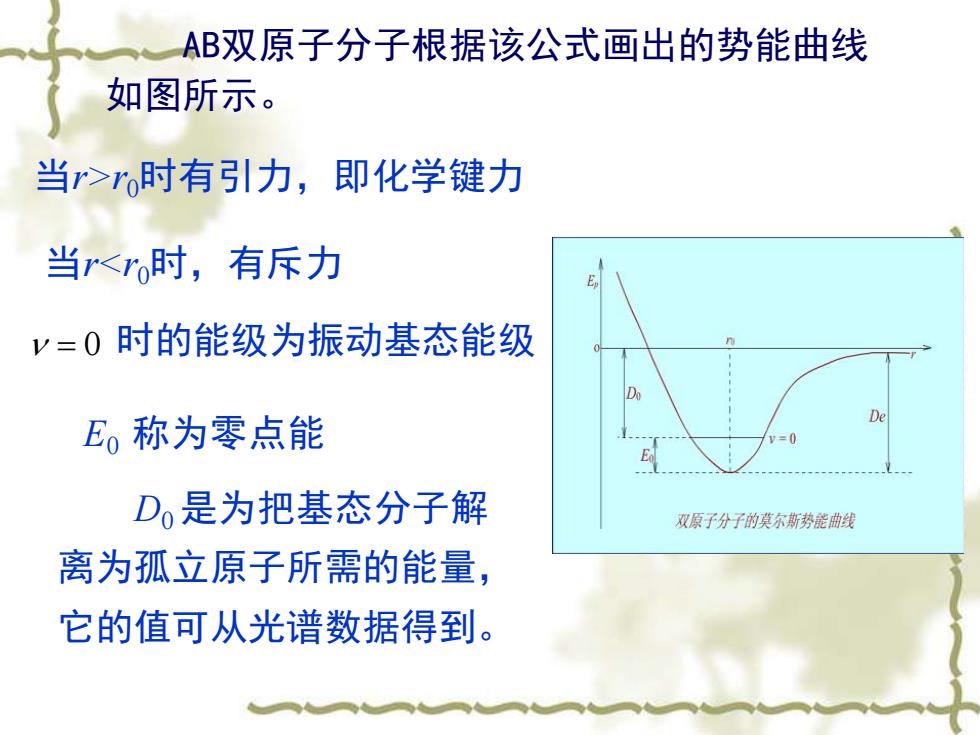
AB双原子分子根据该公式画出的势能曲线 如图所示。 当r>时有引力,即化学键力 当r<时,有斥力 v=0时的能级为振动基态能级 D E,称为零点能 De 20 Do是为把基态分子解 双原子分子的莫尔斯势能曲线 离为孤立原子所需的能量, 它的值可从光谱数据得到
当r>r0时有引力,即化学键力 = 0 时的能级为振动基态能级 AB双原子分子根据该公式画出的势能曲线 如图所示。 当r<r0时,有斥力 D0 是为把基态分子解 离为孤立原子所需的能量, 它的值可从光谱数据得到。 E0 称为零点能