
数据库原理款学课件 关系及相关概念 6.笛卡儿积(续1) M=Πm m,(i=1,2,3,.,n) 设D1={A,B,C;D2={1,2},则D1×D2= {(A,1), (A,2),(B,1),(B,2), (C,1) (C,2)}的基数为:3×2=6。 D D: A 1 DXD2= B A 2 B 1 B 2 C 1 C 2 21
21 关系及相关概念 6.笛卡儿积(续1) 设D1={A,B,C};D2={1,2},则D1×D2 = {(A,1),(A,2),(B,1),(B,2),(C,1), (C,2)}的基数为:3×2=6。 mi (i=1,2,3,.,n) n i i=1 M = m
数据库原理教学课件 2,2.1关系及相关概念 6.笛卡儿积(续2) 笛卡儿乘积可表示为一张二维表,表中的每行对应 个元组,表中的每列对应一个域,但是若干个域的笛卡 儿乘积可能存在大量的数据冗余,因此一般只取其中的 某些子集。笛卡儿乘积的子集就称为关系 表2.6 D,D2,D笛卡儿黍积 。例2.1给出三个域: 产品名称 产地 单价 冰箱 上海 2000 ·D1=家电集合=(冰箱,电视) 冰箱 上海 8000 冰箱 上海 10000 D2=产地集合=(上海,深圳) 10000 冰箱 深圳 2000 D3=单价集合(2000,8000, 冰箱 深圳 8000 冰箱 深圳 10000 则D1XD2×D3笛卡儿乘积为: 电视 上海 2000 电视 上海 8000 电视 上海 10000 电视 深圳 2000 电视 深圳 8000 电视 深圳 10000
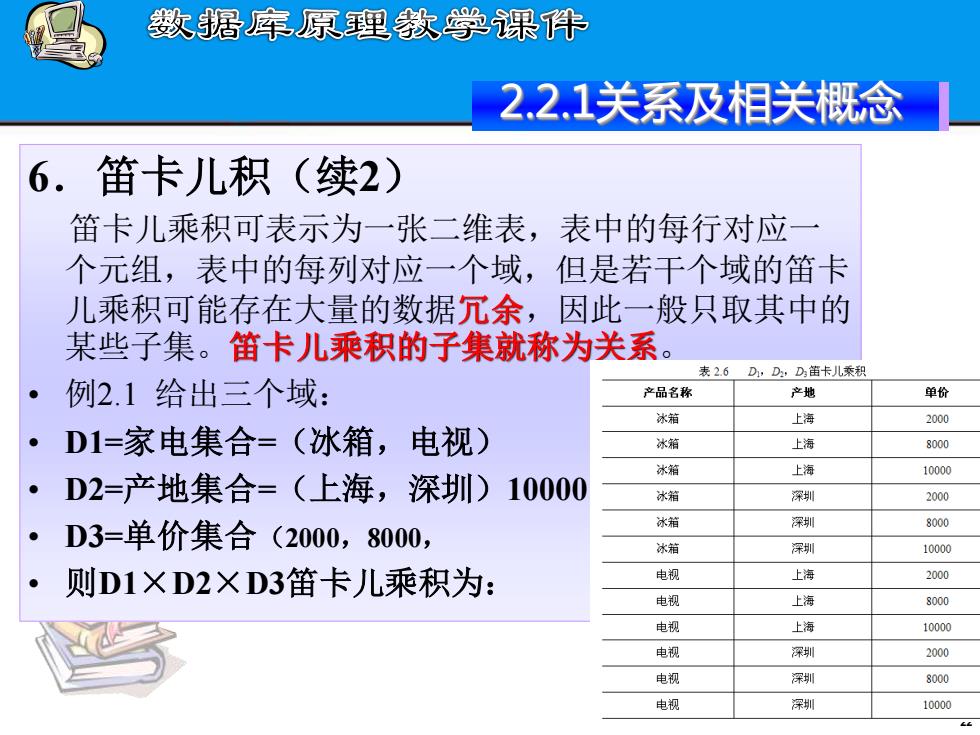
22 2.2.1关系及相关概念 6.笛卡儿积(续2) 笛卡儿乘积可表示为一张二维表,表中的每行对应一 个元组,表中的每列对应一个域,但是若干个域的笛卡 儿乘积可能存在大量的数据冗余,因此一般只取其中的 某些子集。笛卡儿乘积的子集就称为关系。 • 例2.1 给出三个域: • D1=家电集合=(冰箱,电视) • D2=产地集合=(上海,深圳)10000) • D3=单价集合(2000,8000, • 则D1×D2×D3笛卡儿乘积为:

数据库原理款学课件 2.2.1关系及相关概念 7.关系 D1XD2×.Dn的一个子集R称为在域 D1XD2×.Dn上的一个关系(relation),通常 将其表示R(D1XD2X.Dn),其中,R表示该 关系的名称,n称为关系R的元数或度数 (degree),而关系R中所含有的元组数称为R的 基数(cardinal number)。 23
23 2.2.1关系及相关概念 7.关系 D1×D2×.Dn的一个子集R称为在域 D1×D2×.Dn上的一个关系(relation),通常 将其表示R(D1×D2×.Dn),其中,R表示该 关系的名称,n称为关系R的元数或度数 (degree),而关系R中所含有的元组数称为R的 基数(cardinal number)

数据库原理款学课件 2.2.2关系模式 关系模式(Relation Schema)是型 关系是值 。 关系模式是对关系的描述 元组集合的结构 属性构成 属性来自的域 属性与域之间的映象关系 一元组语义以及完整性约束条件 属性间的数据依赖关系集合
24 2.2.2 关系模式 • 关系模式(Relation Schema)是型 • 关系是值 • 关系模式是对关系的描述 – 元组集合的结构 属性构成 属性来自的域 属性与域之间的映象关系 – 元组语义以及完整性约束条件 – 属性间的数据依赖关系集合

数据库原理款学课件 3.定义关系模式 关系模式可以形式化地表示为: R U,D,DOM,F) R 关系名 U 组成该关系的属性名集合 D 属性组U中属性所来自的域 DOM属性向域的映象集合 F 属性间的数据依赖关系集合 25
25 3.定义关系模式 关系模式可以形式化地表示为: R(U,D,DOM,F) R 关系名 U 组成该关系的属性名集合 D 属性组U中属性所来自的域 DOM 属性向域的映象集合 F 属性间的数据依赖关系集合