
海水比热容之大,在所有固体和液体物质中是名列前茅的.世 界大洋的海水总量约1370×10km3,其热容量之大不言而喻。从 热量的传输来看,它对气温变化的影响,无论如何是不能低估的: 海洋性气候优于大陆性气侯,也与此有很大关系。大气的比热容 小,气沿易骤升剧降:陆地的比热容既小,且升降温仅在薄薄的地 表层进行,故温度变化更为烈,海祥则不然,海水的比热容既大, 且因混合效应能涉及相当厚的水层,所以海水温度的变化比较和 缓,总体平均变亿速度,至少比大气小3个量级。 1.4.2体积热能胀 在海水温度高于0(max)的情况下,若海水科吸收热量,除了 会增海水自身的内能之外,还会发生体积膨胀。在框压定盐条作 下,当温度升高K时,单位体积海水的体积的增量,称为体积热 藏张系量(c拉c thermel expmsiun coefficent)或热影胀率(thermal erpansi ny): (1.4-4) 其单位是“开-1”(K),式中是海水的体积,T为热力学程度, T/K=273.15+0/C。米勒罗等已根据国际海水状态方程(见 §1.6)给出了计算m的经验公式。表1一3中最下面的一行,即引 用其计算结果。 海水的体积热膨张系量比纯水的大,并且随水温和盐度的升 高而增大。由表】一3还可看出,在低温低盐时为负值,此即海 水反常膨张的表现。,由负值变为正值之时的温度,就是(mx), 该湿度值随海水盐度的增大而降低。对盐度显著大于0的外海水, 有如下的经验公式(友田好文,高野能三,1990): 8(m4x)=3.95-2.0X10-8-1.1×10-*8 +0.2X10-83 (1.4-5) 22

表1一3在气压为101325P.亲件下海水的 体积热膨张系量(/10-K-) n/C 10 20 30 0 一67 B隐 207 303 10 -30 113 222 31H 20 5 135 237 324 30 36 I57 251 332 35 51.5 166,8 257.0 333.9 非:据发田好文、高1(1990》。 在液态物质中,海水的体积热膨怅系量是比较小的,因而由温 度变化所引起的海水密度的变化,就不太显著,继而由此而产生的 压力梯度也较小,于是由水平温度梯度而产生的德水的运动也比 较弱。这是制约海水运动速度远小于空气的因素之一·。值得注意 的是,海水的体积热膨胀系量随压力的增大而增大,尤其是在低温 时更为明显,例如盐度为35的海水,若温度为0℃,在1000m深处 (海压约为10.tMP.)的体积热膨胀系量,比在海面的值大60× 10~,而温度为20℃时,则仅大×10-。由于高纬海战的水温比 低纬德城低得多,因而上述影响在高纬海城更显著。 1.4.3压缩性、绝热变化及位温 !.证水的压馆性 单位体积的海水,当压力增加1P.时,其体积的负增量称为压 缩系量,若海水微团在被压缩时,因和周围海水有热量交换而得以 维持其水温不变,则称为等温压缩。定盐条件下的等温压缩系量 23

为: =一 (1.4-6) 单位为“帕1”(P阳),式中V为海水的体积,P为压方 股如海水微山作被压第的过程中,与外界没有热量的交换,则 称为绝热压射。定盐条件下的绝热压缩系量为 (1,4-7) 海水的乐缩系量随水温、盐度和压力的增人而减小.与其它液 体相比,海水的正缩系量是较小的,~般小于4.6×10-P.',仅 在低温,纸盐、低压时才人于4,7X10-“P,‘。与海水的体积热膨 账系甚较小相应,这也是导致海水运动速度较小的原因之。鉴 压缩性小,放在动力海洋学中为简化求解,常把海水视为不可乐缩 流你,然而在海洋声学中,压缩系量却是重要的参数。再者,若考 虑到世某大洋的水很深(&】.),其压缩之量就相当可观了。据估 算,若海水果真“不可压缩”的话,那么海平面将比现今高30m左 年。 2.绝热变优 由「海水的压箔系量不为0,故当某·海水做州在海洋中行 船直位移时,时其所处深度变化导致止力不同,就会使其体积发生 相应的变化。在绝热变化时,海水微闭下沉压力增大使其体积缩 小,外力对海水微团作的功,增加了海水微团的内能,导致其福度 于高:反之绝热上升时体积膨帐,则消耗白身内能而导致降温。海 水祖度在绝热变化过程中随压力的变化称为绝热温度梯度(. temperatare gradieut),也行人称为绝热递减米(dinbalc iapse rate》。依 ST及UNESCO(NO.45,1965),绝热温度梯度可用下式计算: F=argT/c (1.4-8) 式中为体积热毖张系量,C,为比定压热容,9为重力加速度,T 24

为热力学温度,由于海洋中的现场压力与水深有关,所以的单位 也可以用“开[尔文]每米#(K/m)。 P是温度、盐度和压力的函数,=(S,0,),可以通过状态方 程和比热容来计算(Bryden,I973),也可以直接测量(Caldwell and Ede,1980).前者提出的多项式的计算结果,与依1980年国际海 水状态方程(SL.6)得出的值相当-一致,因而已被采纳(UNESCO, O.41,1983)。考虑到S1的规定,可将其写成如下形式: 1'8,0,)=ag+a:0+a2心+a购03+(+b0)(8-35) +[cm+c0+c0+G+(d+d0) (8-35)](kp)十(e+e,9+0)() (1.4-9) 式中 a=3.5803×10-5,a,=8.5258×10-6, ag=-6.8360×10-*,a:=6.6228×10-: b0=1.8932×10-5,,=一4.2393×10-4: ca=1.8741X10-',c9=-6.7795X10-0, c=8.7330×10-2,c=-5.4481X10-": d8=-1.1351×10-0.1=2.7759×10-2: e0=4.6206X10-8,=1.8676X10-“, e:=一2.1687X10-6。 8为实用盐标,0为水温(℃,):k=10-‘,为与海压的单位相匹 配的因数。计算结果节录于表1一4中。 3.位温 海水微团从海洋某一深度(压力为)绝热上升到海面(压力 为大气压)时所具有的温度称为位温(pentini temperutre),记为 9.海水微团此时相应的密度,称为位密,记为P。,若该海水微团未 上升之前的现场温度为0,绝热升达海面后温度降低了△0,则该 深度海水的位温即为 25
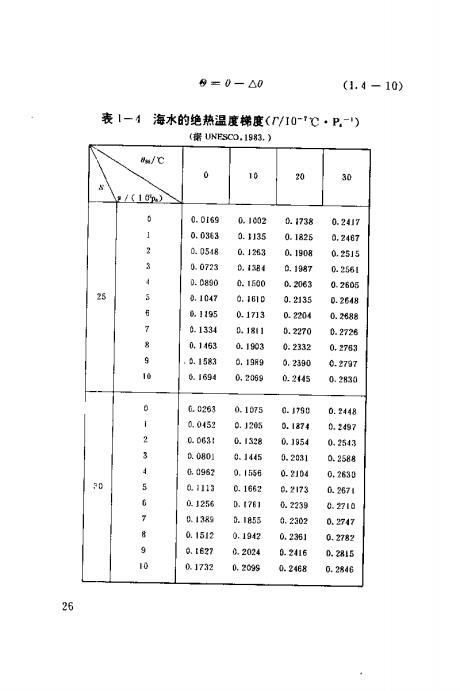
8=0一△0 (1.4-10) 表1一1海水的绝热温度梯度(r/I0-℃·P.-) (据UNESC0.1983.) a/℃ 0 10 20 30 3/(1) 0.0169 0.1002 0.1738 0.2417 1 0.033 0.1135 0.1825 0.2487 0.0548 0.1263 0.1908 0.2515 8 0.0723 0,1384 0.1987 0.2561 0.0890 0.1600 0.2063 0.2605 25 5 0.1047 0.181D 0.2135 0.2648 百 6,1195 0.17]3 0.2204 0.2888 0.1334 0,1811 0.2270 0.2726 8 01453 0.1903 0.2332 0.2763 6.1583 0.19n9 0.2390 0.2797 10 6.1694 0,2069 0.2445 0.2839 0 0.c263 0.1075 0.1790 0.2448 0.0452 0.125 0.1874 0.2497 2 0.063: 0.1328 0.1954 0,2543 0.0801 0.1445 0.2031 0.2588 0.0962 0.1556 0.2104 0.2630 30 5 4.1113 0.1662 0.2173 0.2671 0.1256 0.1761 0.2239 0.2710 0.13R9 0.1855 0.2302 0.2747 0.1512 0.192 0.2361 0.2782 9 Q.t627 0.2024 0.2416 0.2815 10 0.1732 0.209s 0.24e8 0.2846 26