
Project Goals Automate the optimization process and reduce errors ·More realistic model Even novice users can operate Generate better quality solutions in a shorter time MSC Seminar (January 30,2012) Outline 。Domain Description Constraint Programming(CP) ·Problem Modelling 。Improvements 。Concluding Remarks MSC Seminar (January 30,2012) 11
11 MSC Seminar (January 30, 2012) Project Goals • Automate the optimization process and reduce errors • More realistic model • Even novice users can operate • Generate better quality solutions in a shorter time MSC Seminar (January 30, 2012) Outline • Domain Description • Constraint Programming (CP) • Problem Modelling • Improvements • Concluding Remarks

Real-life Applications of CP ·Options trading Gate allocation to aircrafts in airports Selection and scheduling of observations performed by satellites DNA sequencing,construction of 3D models of proteins Locating faults in the circuits,computing circuit layouts,testing and verification of design Many other scheduling,planning and optimization problems MSC Seminar (January 30,2012) Constraint Satisfaction Problems A CSP is a triple <Z,D,C> -Z is a finite set of variables {x1,2,..., -D is a finite set [D,D2,...,D),where D is a finite set of possible values for variable x -C is a set of constraints,each on a subset of Z limiting the possible combinations of values that the variables can take Goal:to find aconsistentv variable assignment MSC Seminar (January 30,2012) 12
12 MSC Seminar (January 30, 2012) Real-life Applications of CP • Options trading • Gate allocation to aircrafts in airports • Selection and scheduling of observations performed by satellites • DNA sequencing, construction of 3D models of proteins • Locating faults in the circuits, computing circuit layouts, testing and verification of design • Many other scheduling, planning and optimization problems MSC Seminar (January 30, 2012) Constraint Satisfaction Problems A CSP is a triple < Z, D, C > – Z is a finite set of variables {x1 , x2 , …, xn } – D is a finite set {D1 , D2 , …, Dn }, where Di is a finite set of possible values for variable xi – C is a set of constraints, each on a subset of Z limiting the possible combinations of values that the variables can take Goal: to find a consistent variable assignment

Confession of a HK Smuggler Take≤9 units and earn≥3白llars Goods Wine Pe M Size 4 units 3 $$ $15 酒 ·var ain y Cap :4W+3P+2C≤9 ·Profit 5W+10P+7C≥30 MSC Seminar(January 30,2012) Constrained Optimization Goods Wine Perfume Cigarettes Size 4 units 3 units 2 units $ $15 $10 $7 ·Constraint: 4W+3P+2C≤9 15W+10P+7C≥30 Objective:15W 10P 7C MSC Seminar (January 30,2012) 13
13 MSC Seminar (January 30, 2012) Take ≤ 9 units and earn ≥ 30 dollars Confession of a HK Smuggler Goods Wine Perfume Cigarettes Size 4 units 3 units 2 units $$$ $15 $10 $7 • Variables {W,P,C} taking domain [0..2], [0..3], [0..4] respectively. • Capacity constraint: 4W + 3P + 2C ≤ 9 • Profit constraint: 15W + 10P + 7C ≥ 30 MSC Seminar (January 30, 2012) Constrained Optimization Objective: 15W + 10P + 7C Goods Wine Perfume Cigarettes Size 4 units 3 units 2 units $$$ $15 $10 $7 • Constraint: 4W + 3P + 2C ≤ 9 15W + 10P + 7C ≥ 30
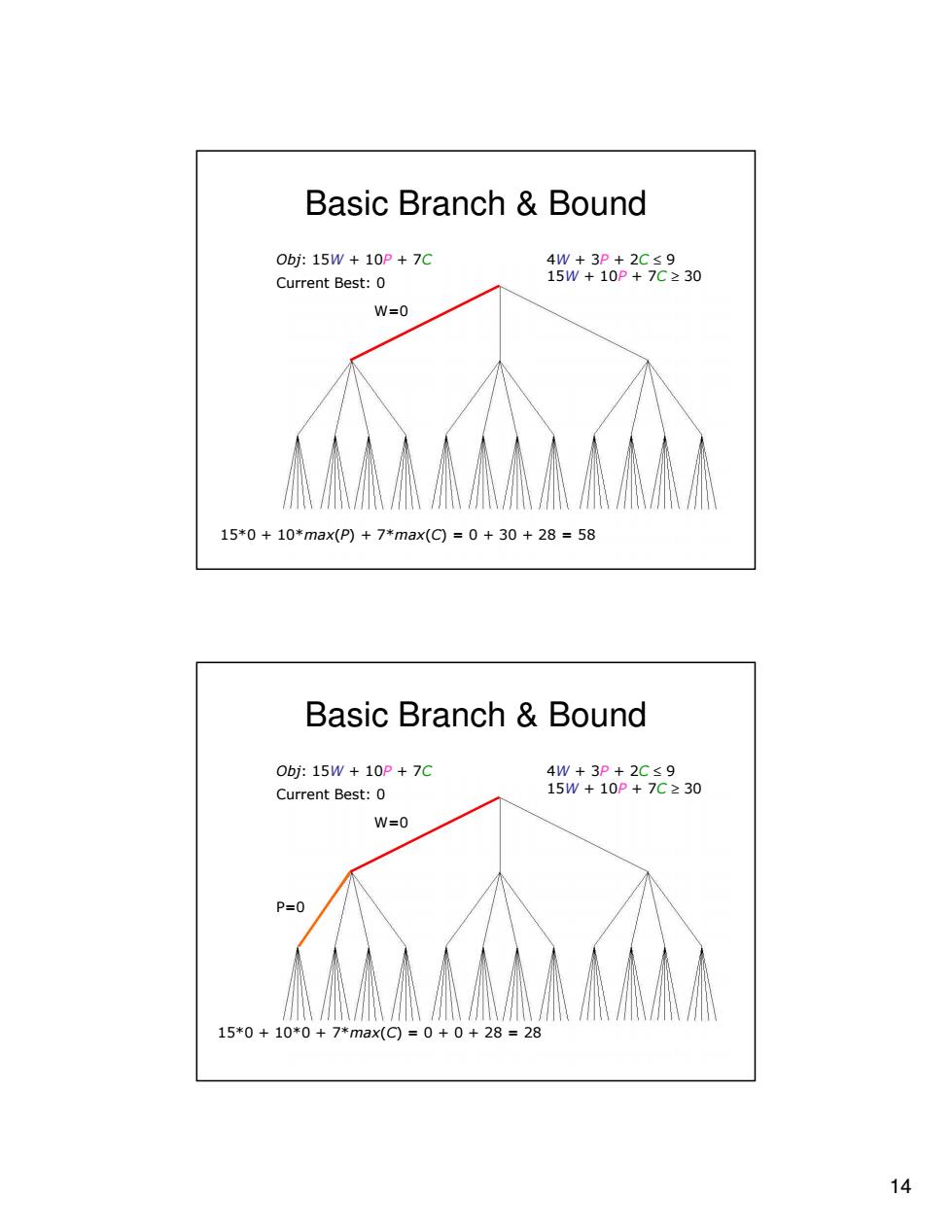
Basic Branch Bound 0bj:15W+10P+7C 4W+3P+2C≤9 Current Best:0 15W+10P+7C230 W=0 15*0+10*max(P)+7*max(C)=0+30+28=58 Basic Branch Bound 0bj:15W+10P+7C 4W+3P+2C≤9 Current Best:0 15W+10P+7C≥30 W=0 P=0 15*0+10*0+7*max(C)=0+0+28=28 14
14 MSC Seminar (January 30, 2012) Obj: 15W + 10P + 7C Current Best: 0 15*0 + 10*max(P) + 7*max(C) = 0 + 30 + 28 = 58 4W + 3P + 2C ≤ 9 15W + 10P + 7C ≥ 30 W=0 Basic Branch & Bound MSC Seminar (January 30, 2012) 15*0 + 10*0 + 7*max(C) = 0 + 0 + 28 = 28 W=0 P=0 Obj: 15W + 10P + 7C Current Best: 0 4W + 3P + 2C ≤ 9 15W + 10P + 7C ≥ 30 Basic Branch & Bound
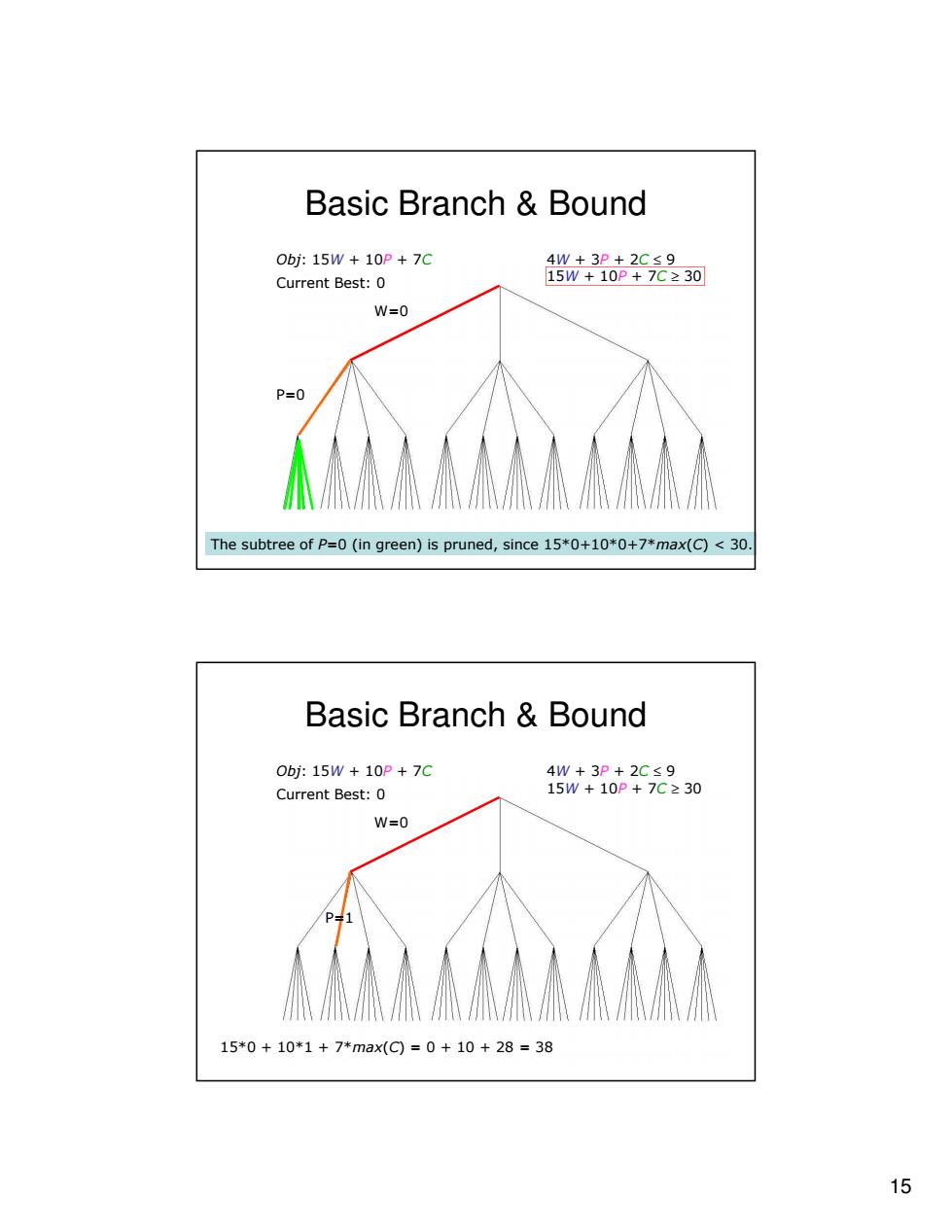
Basic Branch Bound 0bj:15W+10P+7C 4W+3P+2C≤9 Current Best:0 15W+10P+7C230 W=0 P=0 The subtree of P=0(in green)is pruned,since 15*0+10*0+7*max(C)<30. Basic Branch Bound 0bj:15W+10P+7C 4W+3P+2C≤9 Current Best:0 15W+10P+7C≥30 W=0 P=1 15*0+10*1+7*max(C)=0+10+28=38 15
15 MSC Seminar (January 30, 2012) Basic Branch & Bound W=0 P=0 Obj: 15W + 10P + 7C Current Best: 0 4W + 3P + 2C ≤ 9 15W + 10P + 7C ≥ 30 The subtree of P=0 (in green) is pruned, since 15*0+10*0+7*max(C) < 30. MSC Seminar (January 30, 2012) Basic Branch & Bound 15*0 + 10*1 + 7*max(C) = 0 + 10 + 28 = 38 W=0 P=1 Obj: 15W + 10P + 7C Current Best: 0 4W + 3P + 2C ≤ 9 15W + 10P + 7C ≥ 30