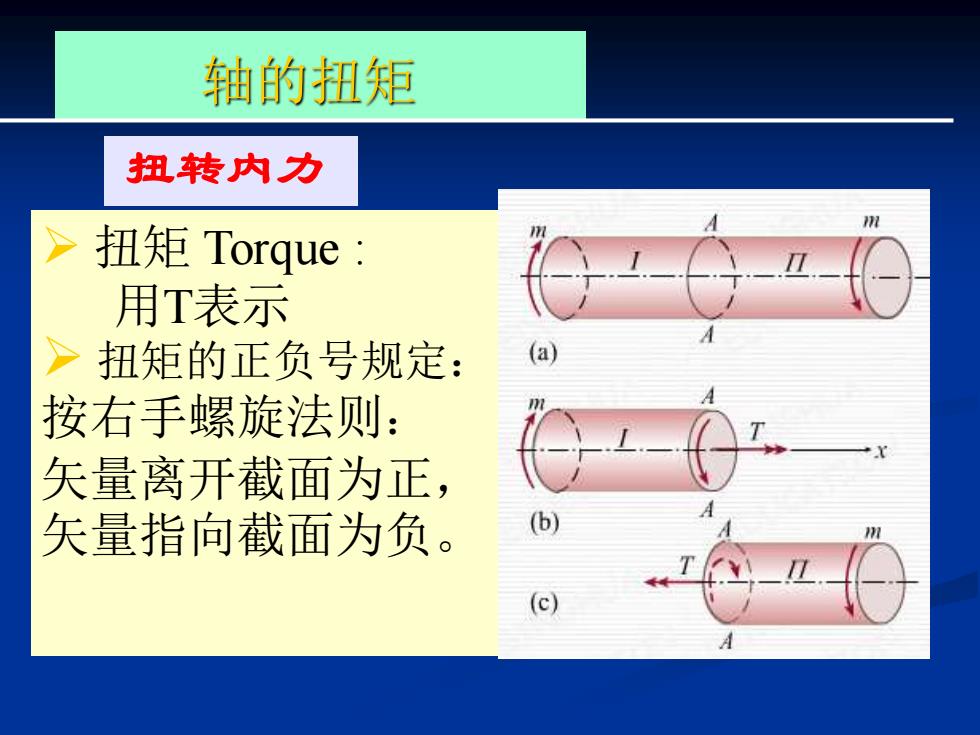
轴的扭矩 扭转内力 > 扭矩Torque 用T表示 >扭矩的正负号规定: 按右手螺旋法则: 矢量离开截面为正, 矢量指向截面为负
轴的扭矩 扭转内力 ➢ 扭矩 Torque : 用T表示 ➢ 扭矩的正负号规定: 按右手螺旋法则: 矢量离开截面为正, 矢量指向截面为负

轴的扭矩图示例 Me Me2 Me3 Me4 ☒ 心法业不该图片 Me4 + Me1 Me1+Me2
(+) (−) 轴的扭矩图示例
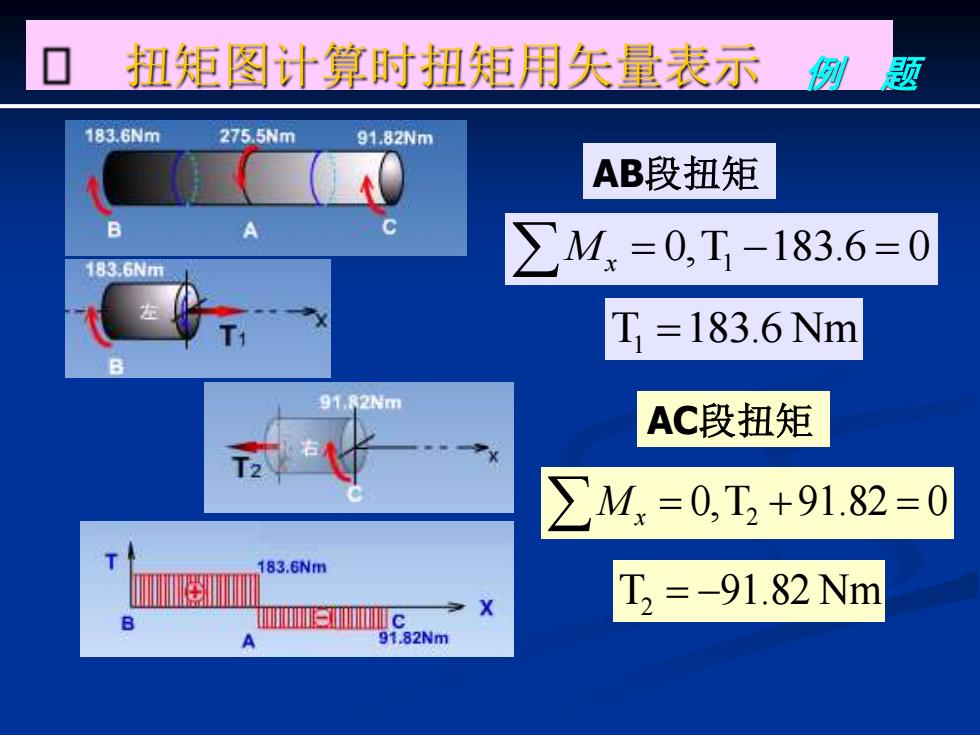
扭矩图计算时扭矩用矢量表示例题 183.6Nm 275.5Nm 91.82Wm AB段扭矩 A 183.6Nm ∑M.=0,T-183.6=0 T=183.6Nm 91.82Nm AC段扭矩 ∑M,=0,T,+91.82=0 183.6Nm T2=-91.82Nm c 9182Nm
扭矩图计算时扭矩用矢量表示 例 题 AB段扭矩 Mx = 0,T1 −183.6 = 0 T1 =183.6 Nm AC段扭矩 = 0,T +91.82 = 0 Mx 2 T2 = −91.82 Nm

§5-2弯曲的概念和内力 •弯曲变形:杆件在垂直于其轴线的载荷作用下,使原为直线的 轴线变为曲线的变形。通常将承受弯曲变形的杆件称为梁。 •对称弯曲:载荷作用在梁的纵向对称平面内。一平面弯曲 P2纵向对称面 杆件轴线 R2 图5-2对称弯曲 (b) 图5-1受弯构件的实例
§5-2 弯曲的概念和内力 •弯曲变形:杆件在垂直于其轴线的载荷作用下,使原为直线的 轴线变为曲线的变形。通常将承受弯曲变形的杆件称为梁。 •对称弯曲:载荷作用在梁的纵向对称平面内。—平面弯曲
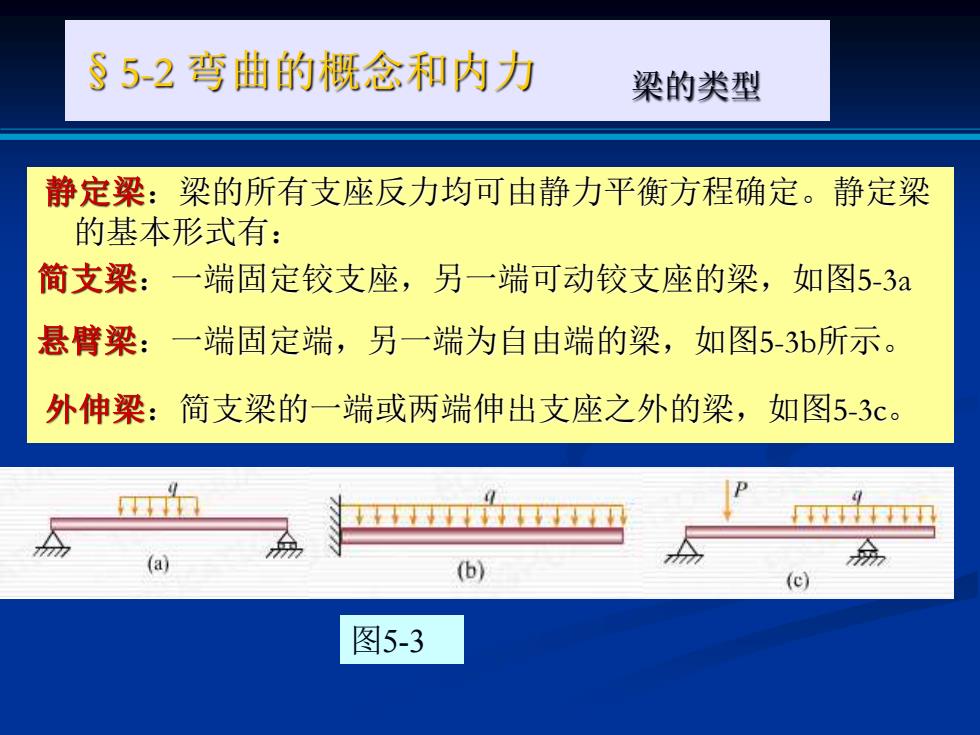
§5-2弯曲的概念和内力 梁的类型 静定梁:梁的所有支座反力均可由静力平衡方程确定。静定梁 的基本形式有: 简支梁:一端固定铰支座,另一端可动铰支座的梁,如图5-3a 悬臂梁:一端固定端,另一端为自由端的梁,如图5-3b所示。 外伸梁:简支梁的一端或两端伸出支座之外的梁,如图5-3c。 (a) (b) 众 (c) 图5-3
§5-2 弯曲的概念和内力 梁的类型 静定梁:梁的所有支座反力均可由静力平衡方程确定。静定梁 的基本形式有: 简支梁:一端固定铰支座,另一端可动铰支座的梁,如图5-3a 悬臂梁:一端固定端,另一端为自由端的梁,如图5-3b所示。 外伸梁:简支梁的一端或两端伸出支座之外的梁,如图5-3c。 图5-3