
例1.1 确定m-m截面上的内力 N=P M-=Pa b a
例1.1 确定m-m截面上的内力 N=P M=Pa

例1直径为d长为1圆截面直杆,铅垂放置,上端 固定,若材料单位体积质量为P,试求因自重引起 杆的m-m截面的内力 o 解: 以2 q=P8- ∑F,=0, FN-gx=0 2 FN =qx- X 4 b) 以2 整个杆件最大的轴力发生 Fy-pe 在固定端截面上,其值: 4
整个杆件最大的轴力发生 在固定端截面上,其值: 例1 直径为 d 长为 l 圆截面直杆,铅垂放置,上端 固定,若材料单位体积质量为 ,试求因自重引起 杆的 m-m 截面的内力 。 解:
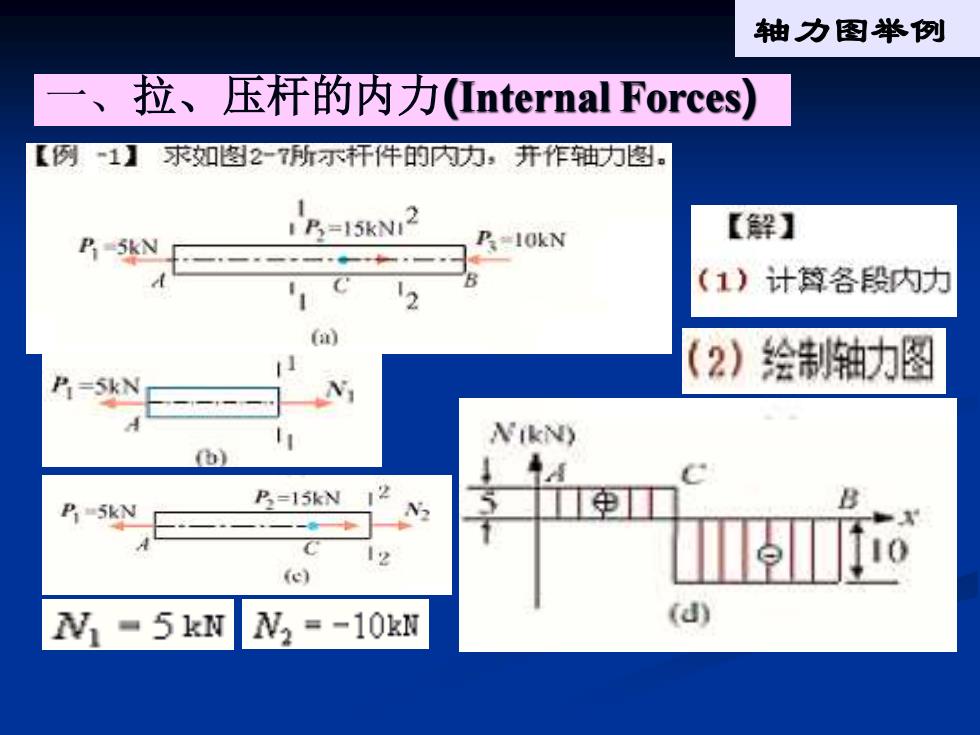
轴力图举例 一、 拉、压杆的内力nternal Forces】 【例1】求如图2~7所示杆件的内内,开作轴力图。 【解】 P=5kN =15kN,2 P-10kN (1)计剪各段内力 2)绘制轴力图 NikN) b P,=15kN 112 一一 (e) N-5kN N2=-10kN (d)
一、拉、压杆的内力(Internal Forces) 轴力图举例
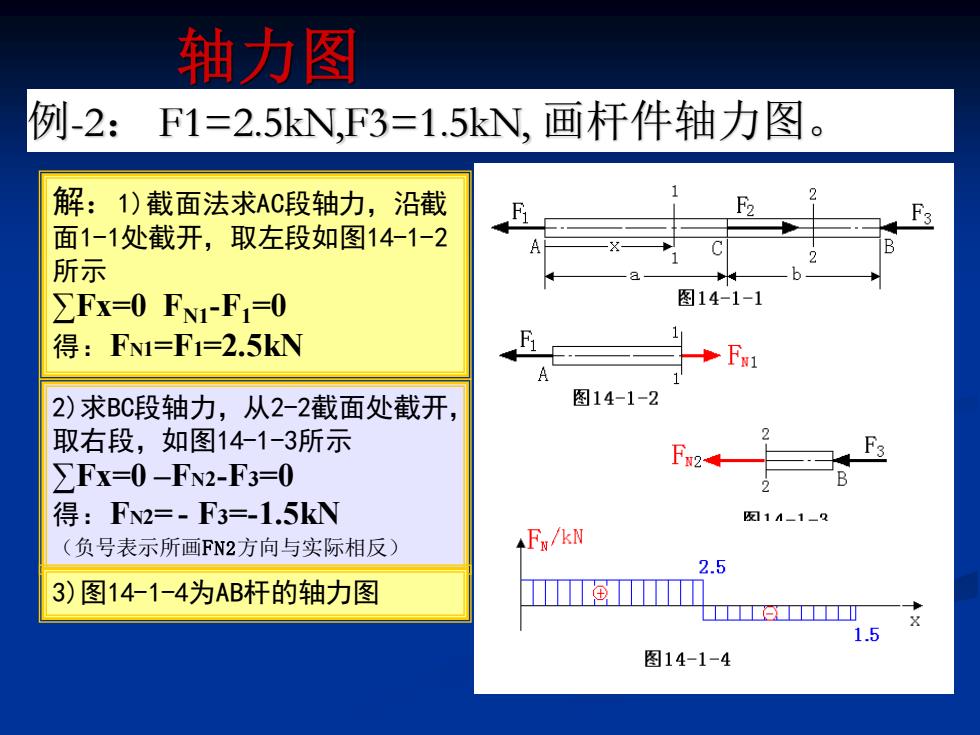
轴力图 例-2:F1=2.5kN,F3=1.5kN,画杆件轴力图。 解:1)截面法求AC段轴力,沿截 面1-1处截开,取左段如图14-1-2 所示 ∑Fx=0FN-F1=0 图14-1-1 得:FN1=F1=2.5kN 1 +F1 2)求BC段轴力,从2-2截面处截开, 图14-1-2 取右段,如图14-1-3所示 2 F3 ∑Fx=0-FN2-F3=0 得:F2=-F3=-1.5kN 凤1-1-2 (负号表示所画FN2方向与实际相反) Fx/kN 2.5 3)图14-1-4为AB杆的轴力图 1.5 图14-1-4
轴力图 例-2: F1=2.5kN,F3=1.5kN, 画杆件轴力图。 解:1)截面法求AC段轴力,沿截 面1-1处截开,取左段如图14-1-2 所示 ∑Fx=0 FN1-F1=0 得:FN1=F1=2.5kN 2)求BC段轴力,从2-2截面处截开, 取右段,如图14-1-3所示 ∑Fx=0 –FN2-F3=0 得:FN2= - F3=-1.5kN (负号表示所画FN2方向与实际相反) 3)图14-1-4为AB杆的轴力图

轴力图举例 例题2-3 11 B 12 c 3 D 已知F=10kN;F)=20kN; F3=35kWN;F25kN;试画 F 出图示杆件的轴力图。 1F22F3 解:1、计算各段的轴力。 →Fw AB段 ∑F=0 FNI=F=10kN -FN2 BC段 F2 ∑F=0F2+E=F FN2=F-F2= 10-20=-10kN F (kN) 10 CD段 ∑F=0 FN3 F =25kN 2、绘制轴力图
已知F1=10kN;F2=20kN; F3=35kN;F4=25kN;试画 出图示杆件的轴力图。 1 1 Fx = 0 FN1 = F1 =10kN 例题2-3 FN1 F1 解:1、计算各段的轴力。 F1 F2 F3 F4 A B C D AB段 10 20 10kN 2 1 2 − = − FN = F − F = BC段 2 2 3 3 FN3 F4 FN2 F1 F2 Fx = 0 FN2 + F2 = F1 Fx = 0 FN3 = F4 = 25kN CD段 2、绘制轴力图。 (kN) FN x 10 25 10 (+) (−) (+) 轴力图举例