
2-3.任意力系的简化
2-3. 任意力系的简化

2-3-1力向一点平移定理 1.实例
2024-10-1 F F-F F
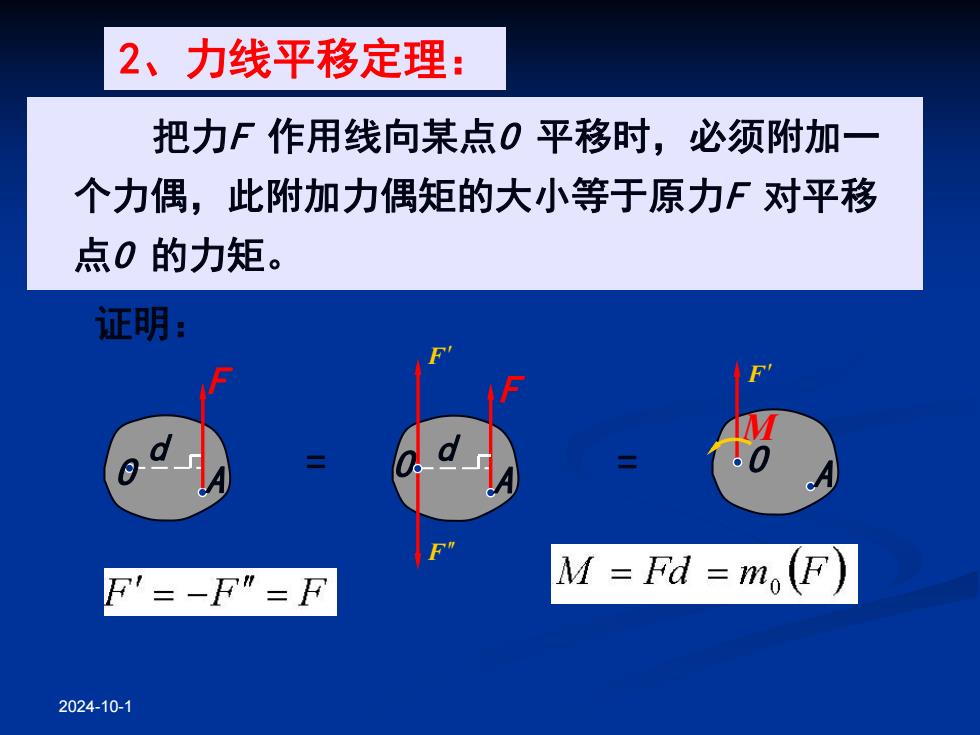
2、力线平移定理: 把力F作用线向某点0平移时,必须附加一 个力偶,此附加力偶矩的大小等于原力F对平移 点0的力矩。 证明: F'=-F"=F M=Fd =mo(F) 2024-10-1
2024-10-1 F O A d F A O d F F M A O F = = 把力F 作用线向某点O 平移时,必须附加一 个力偶,此附加力偶矩的大小等于原力F 对平移 点O 的力矩。 证明: 2、力线平移定理:
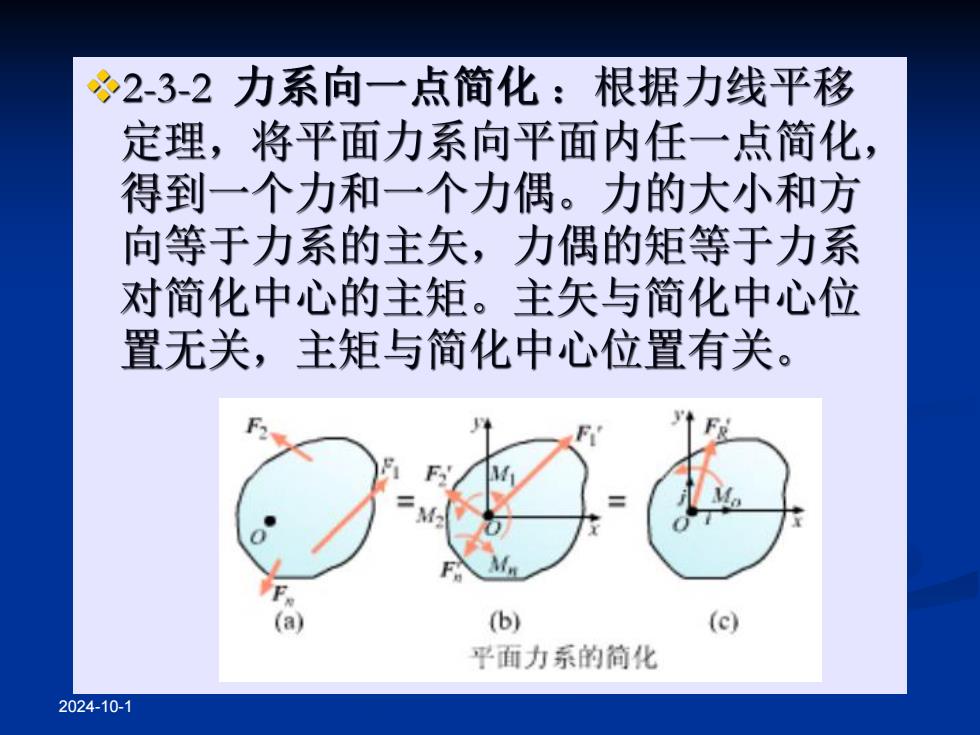
冬23-2力系向一点简化:根据力线平移 定理,将平面力系向平面内任一点简化, 得到一个力和一个力偶。力的大小和方 向等于力系的主矢,力偶的矩等于力系 对简化中心的主矩。主矢与简化中心位 置无关,主矩与简化中心位置有关。 (a) (b) (c) 平面力系的简化 2024-10-1
2024-10-1
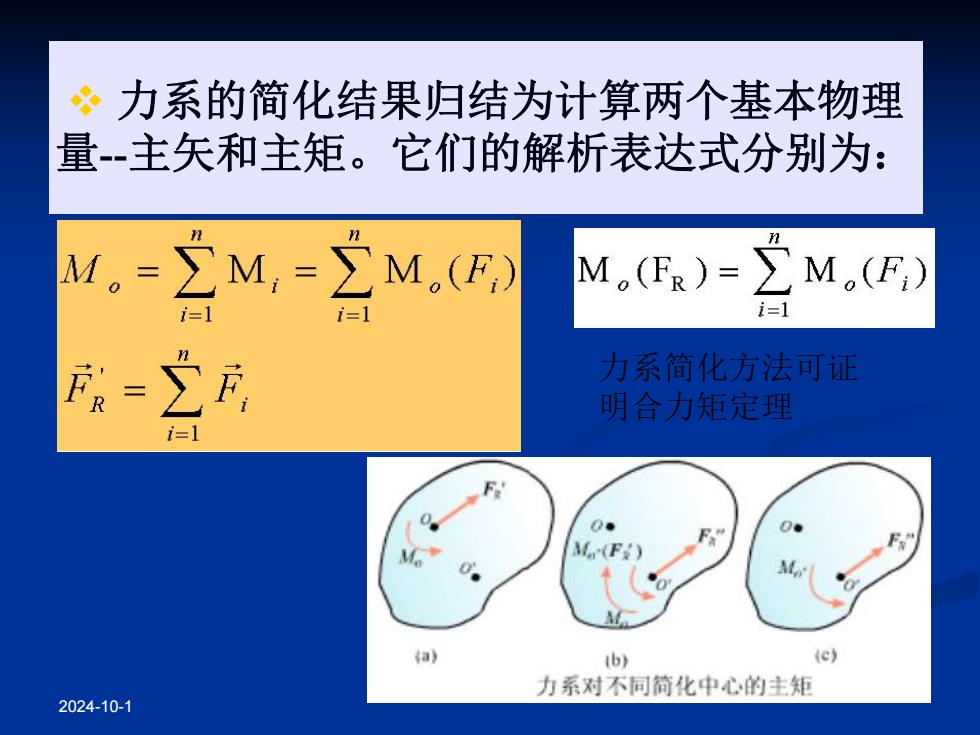
?力系的简化结果归结为计算两个基本物理 量-主矢和主矩。它们的解析表达式分别为: M。=∑M,=∑M,(E,) M,(FR)=∑M,(F) i=1 i=1 =】 力系简化方法可证 明合力矩定理 i=1 Q. M(F) a ib) (e) 力系对不同简化中心的主矩 2024-10-1
2024-10-1 v 力系的简化结果归结为计算两个基本物理 量-主矢和主矩。它们的解析表达式分别为: 力系简化方法可证 明合力矩定理