
将基带信号与载波信号cosw。t相乘,就变为一个带通信号; x() x(t)=x(t)cos2πft X(f f cos2πft fm fm=1/T X(f) 基带信 号带宽 f -fc fe-fmf。fe+fm 带通信 号带宽
将基带信号与载波信号coswct相乘,就变为一个带通信号; 带通信 号带宽 |Xc(f)| f -fc fc-fm fc fc+fm |X(f)| -fm fm f 基带信 号带宽 x(t) cos2πfct xc(t)=x(t)cos2πfct fm=1/T

带宽(bandwidth) 问题 8专 带宽这个名词在通信中经常出现,实际中可能有两种不同含义的带宽:一 种是信号的带宽,这是由信号能量谱密度或功率谱密度在频域的分布规律 确定的,也是我们下面重点讨论的;另一种是信道的带宽,这是由传输电 路的传输特性决定的。因此,工作中要分清! 义 由于时-频关系,我们知道,带宽受限的信号,时域上是无限的;时域有限 的信号,带宽又是无限的。 。从理论上讲,除极个别信号外,信号的频谱都是分布得无穷宽的。如前面 矩形脉冲的频谱。如果把凡是有信号频谱的范围都算带宽,那很多信号的 带宽都是无穷大,显然这样定义带宽是不合适的。一般信号虽然频谱很宽, 但绝大部分实用信号的主要能量(功率)都集中在某一个不太宽的频率范 围内,因此通常根据信号能量(功率)集中的情况,恰当地定义信号带宽。 在实际应用中,常用功率谱密度的带宽给随机信号分类,如基带随机信号、 带通随机信号等;此外,有些噪声也用功率谱密度进行分类,如白噪声、 有色噪声等
带宽(bandwidth)问题 带宽这个名词在通信中经常出现,实际中可能有两种不同含义的带宽:一 种是信号的带宽,这是由信号能量谱密度或功率谱密度在频域的分布规律 确定的,也是我们下面重点讨论的;另一种是信道的带宽,这是由传输电 路的传输特性决定的。因此,工作中要分清! 由于时-频关系,我们知道,带宽受限的信号,时域上是无限的;时域有限 的信号,带宽又是无限的。 从理论上讲,除极个别信号外,信号的频谱都是分布得无穷宽的。如前面 矩形脉冲的频谱。如果把凡是有信号频谱的范围都算带宽,那很多信号的 带宽都是无穷大,显然这样定义带宽是不合适的。一般信号虽然频谱很宽, 但绝大部分实用信号的主要能量(功率)都集中在某一个不太宽的频率范 围内,因此通常根据信号能量(功率)集中的情况,恰当地定义信号带宽。 在实际应用中,常用功率谱密度的带宽给随机信号分类,如基带随机信号、 带通随机信号等;此外,有些噪声也用功率谱密度进行分类,如白噪声、 有色噪声等
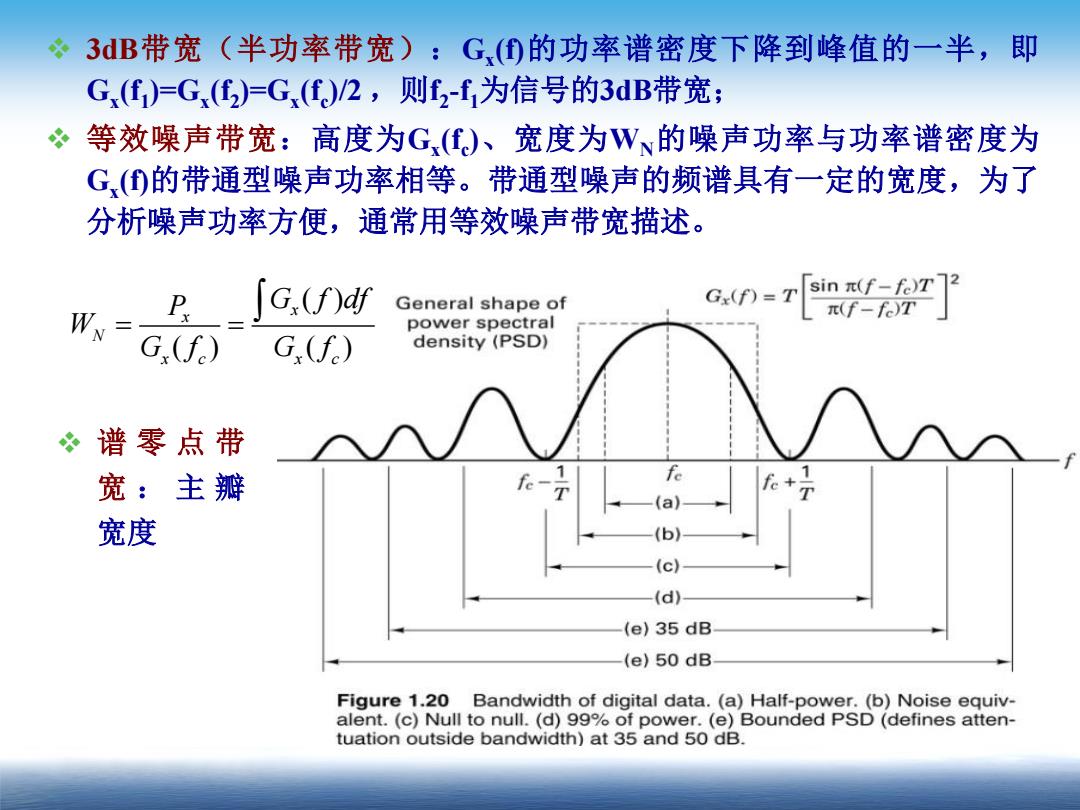
÷3B带宽(半功率带宽):G(①的功率谱密度下降到峰值的一半,即 G()=G(2)=G()/2,则2-f为信号的3dB带宽; 8 等效噪声带宽:高度为G()、宽度为W、的噪声功率与功率谱密度为 G()的带通型噪声功率相等。带通型噪声的频谱具有一定的宽度,为了 分析噪声功率方便,通常用等效噪声带宽描述。 ∫G,(f)d General shape of Gx(f)=T sinπ(f-fe)T2 π(f-f)T」 power spectral G(f) G(f) density (PSD) 冬谱零点带 宽:主瓣 -(a 宽度 (c) (d) (e)35 dB (e)50 dB Figure 1.20 Bandwidth of digital data.(a)Half-power.(b)Noise equiv- alent.(c)Null to null.(d)99%of power.(e)Bounded PSD(defines atten- tuation outside bandwidth)at 35 and 50 dB
3dB带宽(半功率带宽):Gx (f)的功率谱密度下降到峰值的一半,即 Gx (f1 )=Gx (f2 )=Gx (fc )/2 ,则f2 -f1为信号的3dB带宽; 等效噪声带宽:高度为Gx (fc )、宽度为WN的噪声功率与功率谱密度为 Gx (f)的带通型噪声功率相等。带通型噪声的频谱具有一定的宽度,为了 分析噪声功率方便,通常用等效噪声带宽描述。 ( ) ( ) ( ) x x N x c x c P G f df W G f G f 谱 零 点 带 宽 : 主 瓣 宽度

常用分布函数 二项分布:如果随机变量取值只能是a、b两个值中的一个,设取a的概 率为p,取b的概率为q,在n个结果中,如果k个结果等于a,则其分布 函数为: P,(5=k)= kp'g (0≤k≤n,p+q=1) 其均值、方差分布为E(5)=np,D(5)=np9 Binomial Cumulative Distribution Binomial Probability Density 0.5 0.5 0 0 -2 -1.5-1 -0.50 0.51 1.52 -2 -1.5-1 -0.500.511.5 2
常用分布函数 二项分布:如果随机变量取值只能是a、b两个值中的一个,设取a的概 率为p,取b的概率为q,在n个结果中,如果k个结果等于a,则其分布 函数为: 其均值、方差分布为 ( ) (0 , 1) k n k b n P k p q k n p q k E np D npq ( ) , ( ) -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 0.5 1 Binomial Cumulative Distribution -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 0.5 1 Binomial Probability Density
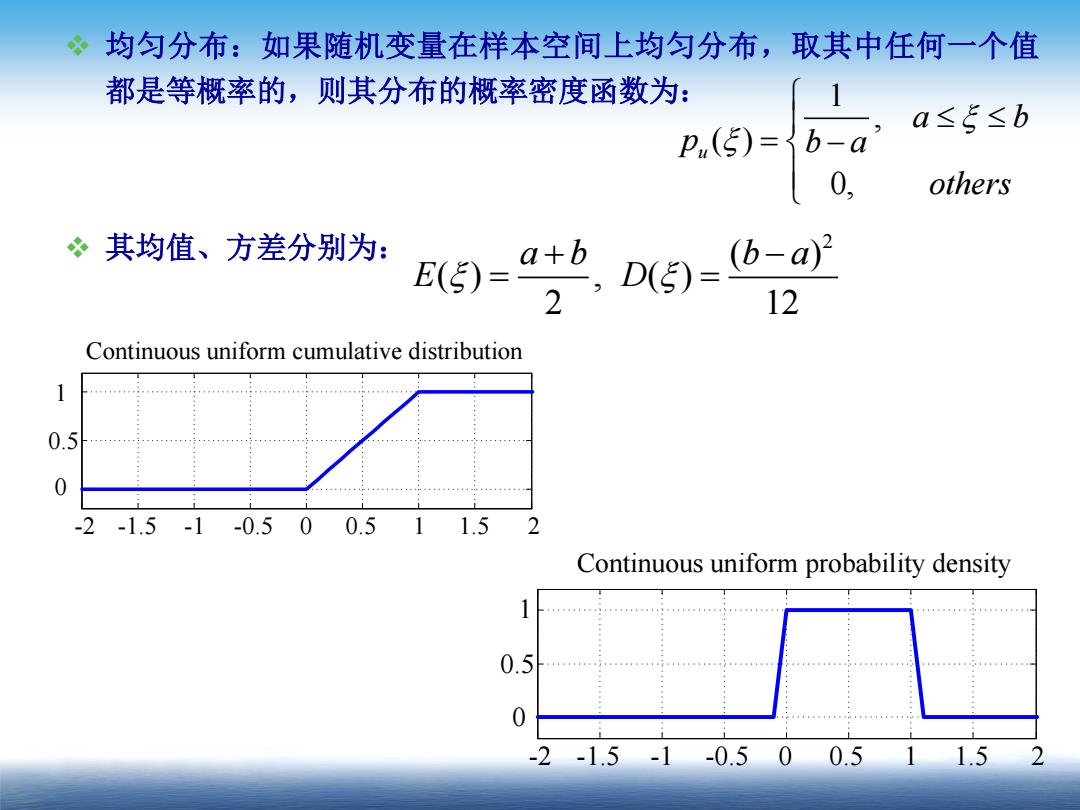
均匀分布:如果随机变量在样本空间上均匀分布,取其中任何一个值 都是等概率的,则其分布的概率密度函数为: 1 p,(5)=b-a a≤5≤b 0, others 其均值、方差分别为: 12 Continuous uniform cumulative distribution 0.5 0 -2-1.5-1-0.500.511.52 Continuous uniform probability density 0.5 0 -2-1.5-1-0.50 0.5 1.5
均匀分布:如果随机变量在样本空间上均匀分布,取其中任何一个值 都是等概率的,则其分布的概率密度函数为: 其均值、方差分别为: 1 , ( ) 0, u a b p b a others 2 ( ) ( ) , ( ) 2 12 a b b a E D -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 0.5 1 Continuous uniform cumulative distribution 0 0.5 1 Continuous uniform probability density -2 -1.5 -1 -0.5 0 0.5 1 1.5 2