
(1)直线方程式 y=bo+bix y:产量,bo:施肥前产量水平,b系数 特征:固定报酬,因而该式不能反映当施肥量递 增时表现出的肥效递减现象以及过量施肥,特别 是过量施用N肥时的总产量下降现象。 存在条件:在较低生产水平、较低肥力、施用低 量肥料时,可能符合直线方程
(1)直线方程式 y=b0+b1x y:产量,b0:施肥前产量水平,b1系数 特征:固定报酬,因而该式不能反映当施肥量递 增时表现出的肥效递减现象以及过量施肥,特别 是过量施用N肥时的总产量下降现象。 存在条件:在较低生产水平、较低肥力、施用低 量肥料时,可能符合直线方程
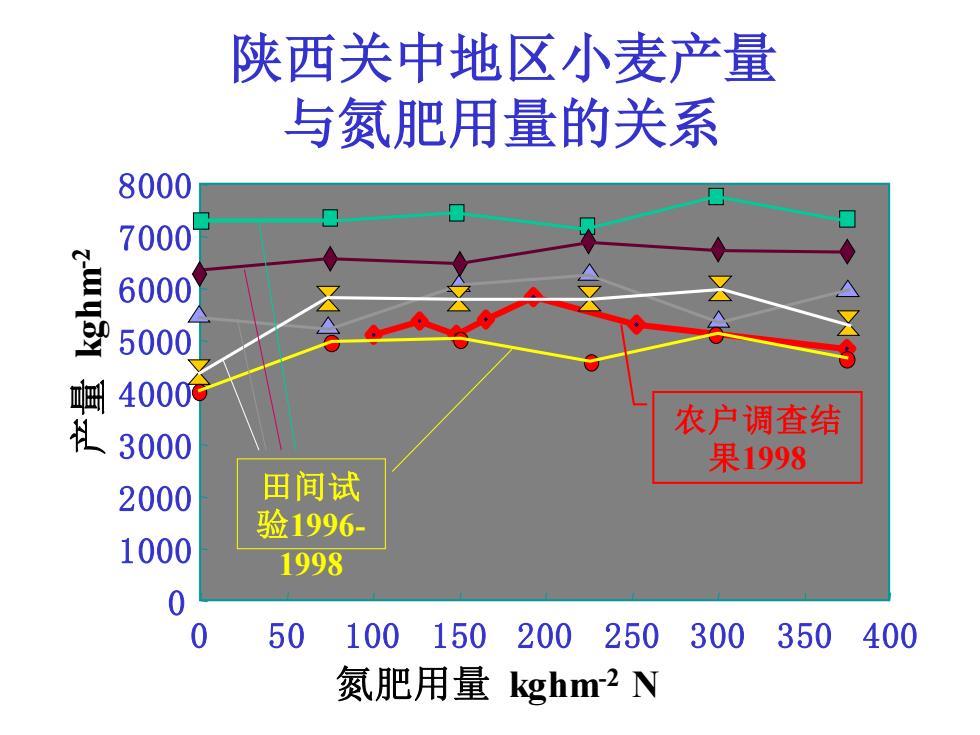
陕西关中地区小麦产量 与氮肥用量的关系 8000 7000 6000 5000 响4000 农户调查结 3000 果1998 2000 田间试 验1996- 1000 1998 0 0 50 100150200 250300350400 氮肥用量kghm2N
陕西关中地区小麦产量 与氮肥用量的关系 0 1000 2000 3000 4000 5000 6000 7000 8000 0 50 100 150 200 250 300 350 400 氮肥用量 kghm-2 N 产量 kghm- 2 农户调查结 果1998 田间试 验1996- 1998

(2)指数(或对数)方程式 1米采利希方程式 由米氏于1909年提出: 对数式为: 1g(A-y)=1gA-cx 指数式为: y=A(1-10-cx) A为增施某一养分可以达到的最高产量,y为养分为x时的实 际产量,C为效应系数。C值愈大,达到一定产量需要的施 肥量愈少,肥料的增产效应愈高
(2)指数(或对数)方程式 i 米采利希方程式 由米氏于1909年提出: 对数式为: lg(A-y)=lgA-cx 指数式为: y=A(1-10-cx) A为增施某一养分可以达到的最高产量,y为养分为x时的实 际产量,C为效应系数。 C值愈大,达到一定产量需要的施 肥量愈少,肥料的增产效应愈高

ii典型的指数方程式 米氏方程中X为养分供应量,包括了土壤养分,不能直 观表达施肥量的影响,为此,克劳斯等提出了修正式,并称 之为典型的指数方程式。 y=yo+d(1-10-cx) yo为不施肥产量 d为最大产量 k为效应系数 iii斯皮尔曼(Spillman)方程式 y=A(1-Rx)
ii典型的指数方程式 米氏方程中X为养分供应量,包括了土壤养分,不能直 观表达施肥量的影响,为此,克劳斯等提出了修正式,并称 之为典型的指数方程式。 y=y0+d(1-10-cx) y0为不施肥产量 d为最大产量 k为效应系数 iii斯皮尔曼(Spillman)方程式 y=A(1-R x)

指数方程式特征:①报酬递减 ②反映最高产量以前的效应 指数方程式都存在一个共同的缺点,即肥料用量没 有超过最高产量施肥量,它们不能反映总产量因施 肥量增加而下降的那部分效应关系
指数方程式特征:①报酬递减 ②反映最高产量以前的效应 指数方程式都存在一个共同的缺点,即肥料用量没 有超过最高产量施肥量,它们不能反映总产量因施 肥量增加而下降的那部分效应关系