Algorithm by an example W1>W2>W3>W4 mi W1 m3>m1>m2>m4 W1>W2>W3>W4 m2 W2 m3>m4>m1>m2 W2>W1>W3>W4 m3 W3 m1>m4>m2>m3 W3>W2>W4>W1 m4 W4 m4>m1>m3>m2 16
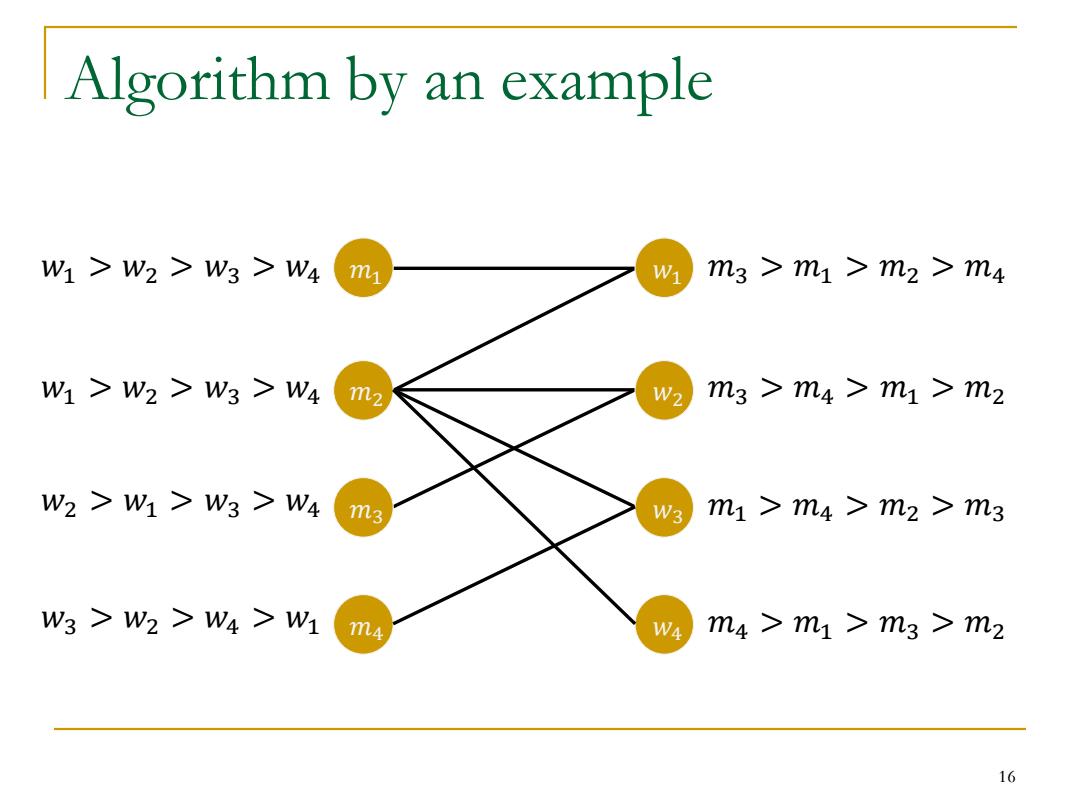
Algorithm by an example 𝑚3 > 𝑚1 > 𝑚2 > 𝑚4 𝑚3 > 𝑚4 > 𝑚1 > 𝑚2 𝑚1 > 𝑚4 > 𝑚2 > 𝑚3 𝑚4 > 𝑚1 > 𝑚3 > 𝑚2 𝑤1 > 𝑤2 > 𝑤3 > 𝑤4 𝑚1 𝑤1 𝑤1 > 𝑤2 > 𝑤3 > 𝑤4 𝑤2 > 𝑤1 > 𝑤3 > 𝑤4 𝑤3 > 𝑤2 > 𝑤4 > 𝑤1 𝑚2 𝑚3 𝑚4 𝑤2 𝑤3 𝑤4 16

Gale-Shapley (Deferred-Acceptance) Algorithm Initially all men and women are free while there is a man m who is free and hasn't proposed to every woman choose such a man m arbitrarily 0 let w be the highest ranked woman in m's preference list to whom m hasn't proposed yet ▣∥next:m proposes to w a if w is free,then (m,w)become engaged 口 else,suppose w is currently engaged to m' if w prefers m'to m,then m remains free if w prefers m to m',then (m,w)becomes engaged and m' becomes free Return the set of engaged pairs as a matching 17
Gale-Shapley (Deferred-Acceptance) Algorithm ◼ Initially all men and women are free ◼ while there is a man 𝑚 who is free and hasn’t proposed to every woman ❑ choose such a man 𝑚 arbitrarily ❑ let 𝑤 be the highest ranked woman in 𝑚’s preference list to whom 𝑚 hasn’t proposed yet ❑ // next: 𝑚 proposes to 𝑤 ❑ if 𝑤 is free, then (𝑚, 𝑤) become engaged ❑ else, suppose 𝑤 is currently engaged to 𝑚′ ◼ if 𝑤 prefers 𝑚′ to 𝑚, then 𝑚 remains free ◼ if 𝑤 prefers 𝑚 to 𝑚′ , then (𝑚, 𝑤) becomes engaged and 𝑚′ becomes free ◼ Return the set of engaged pairs as a matching 17