
复 轴向拉压 扭转 弯曲 NL T·b 变形 △L= EA G·Ip Ef(x)”=-M 刚度条件 △L 180 L GIp =[o1 t sIf]er slo π 虎克定律 0= Ea GY 超静定 1、静平衡方程 问题 2、变形协调方程
变形 刚度条件 EA NL L= P G I T L = = max 180 GIP T EIf (x) = −M(x) max max f f 轴向拉.压 扭 转 弯 曲 L L = 虎克定律 = E = G 超静定 问题 1、静平衡方程 2、变形协调方程
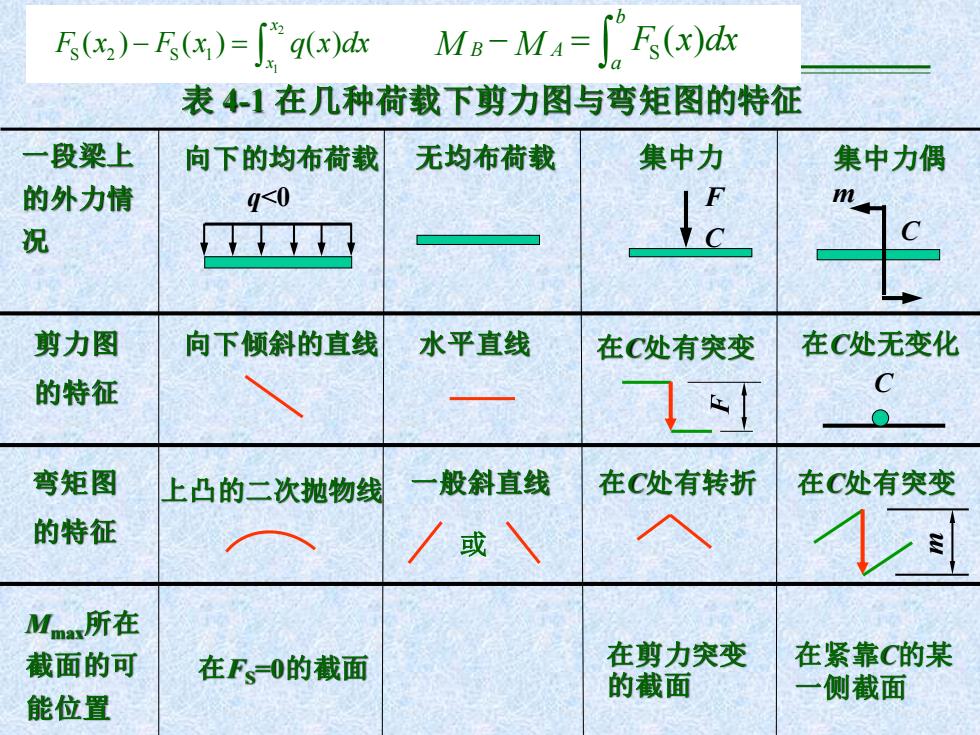
E(3)-E(x)=∫qx)d Ma-M=[F(x)dx 表41在几种荷载下剪力图与弯矩图的特征 一段梁上 向下的均布荷载 无均布荷载 集中力 集中力偶 的外力情 4<0 况 剪力图 向下倾斜的直线 水平直线 在C处有突变 在C处无变化 的特征 弯矩图 上凸的二次抛物线 一般斜直线 在C处有转折 在C处有突变 的特征 /或、 Mmas所在 截面的可 在F、O的截面 在剪力突变 在紧靠C的某 的截面 一侧截面 能位置
无均布荷载 集中力 F C 集中力偶 m C 向下倾斜的直线 上凸的二次抛物线 在FS=0的截面 水平直线 一般斜直线 或 在C处有转折 在剪力突变 的截面 在紧靠C的某 一侧截面 一段梁上 的外力情 况 剪力图 的特征 弯矩图 的特征 Mmax所在 截面的可 能位置 表 4-1 在几种荷载下剪力图与弯矩图的特征 q<0 向下的均布荷载 在C处有突变 在C处有突变 m 在C处无变化 C S ( ) b B A a M M− = F x dx 2 1 S 2 S 1 ( ) ( ) ( ) x x F x F x q x dx − =
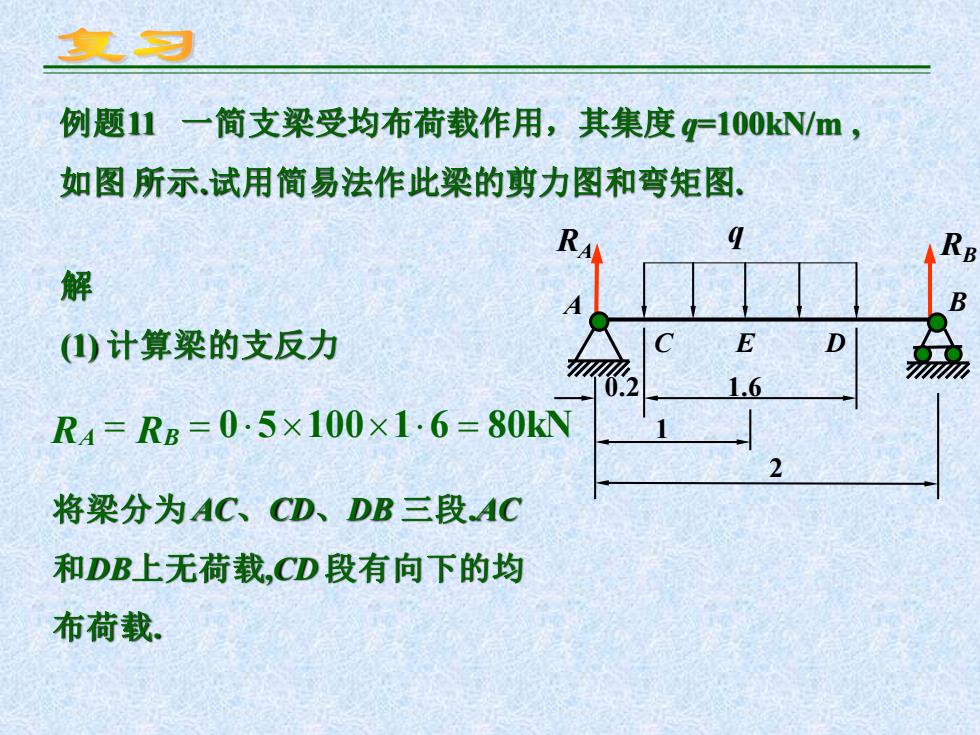
复习 例题11 一简支梁受均布荷载作用,其集度g一100kN/m, 如图所示试用简易法作此梁的剪力图和弯矩图. RA 9 解 (①)计算梁的支反力 E 0.2 1.6 R4=RB=0.5×100×1·6=80kN 将梁分为AC、CD、DB三段AC 和DB上无荷载,CD段有向下的均 布荷载
例题11 一简支梁受均布荷载作用,其集度q=100kN/m , 如图 所示.试用简易法作此梁的剪力图和弯矩图. 解 (1) 计算梁的支反力 RA RB E q A B C D 0.2 1.6 1 2 RA = RB = 0510016 = 80kN 将梁分为 AC、CD、DB 三段.AC 和DB上无荷载,CD 段有向下的均 布荷载
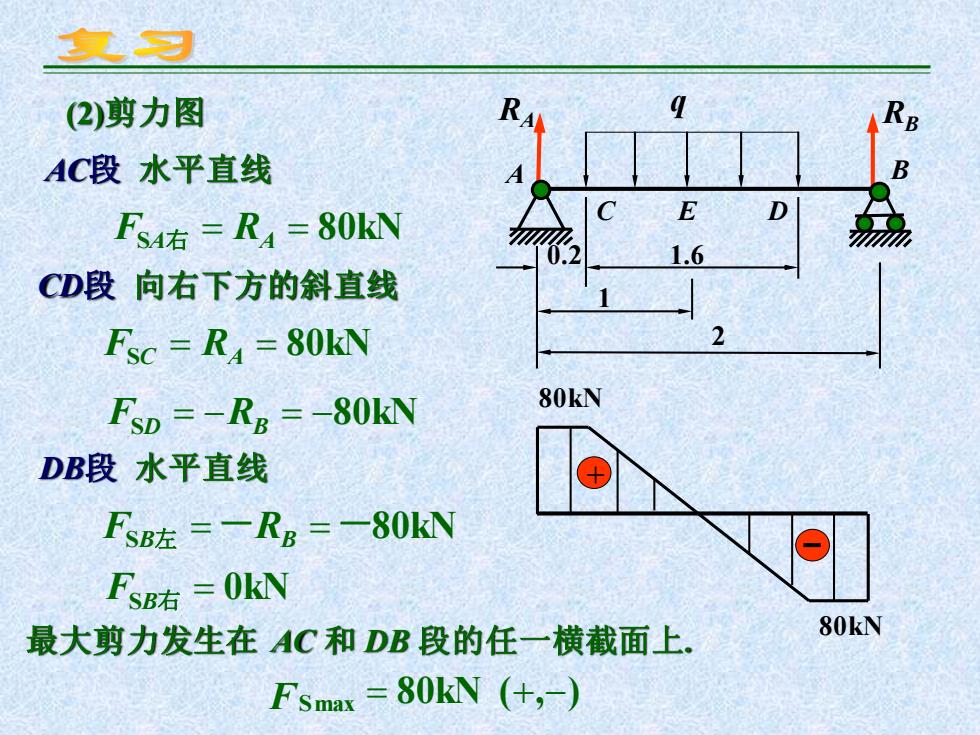
复习 (2)剪力图 AC段水平直线 A F4右=R4=80kN 1.6 CD段向右下方的斜直线 FSC =R4=80kN FSD =-RB =-80kN 80kN DB段水平直线 FsB左=-Rg=一80kN FsB右=0kN 最大剪力发生在AC和DB段的任一横截面上 80kN Fsmax=80kN (+,-
(2)剪力图 + 80kN 80kN AC段 水平直线 FSA右 = RA = 80kN CD段 向右下方的斜直线 FSC = RA = 80kN FSD = −RB = −80kN DB段 水平直线 FSB左 =-RB =-80kN FSB右 = 0kN 最大剪力发生在 AC 和 DB 段的任一横截面上. max 80kN ( , ) FS = + − RA RB E q A B C D 0.2 1.6 1 2
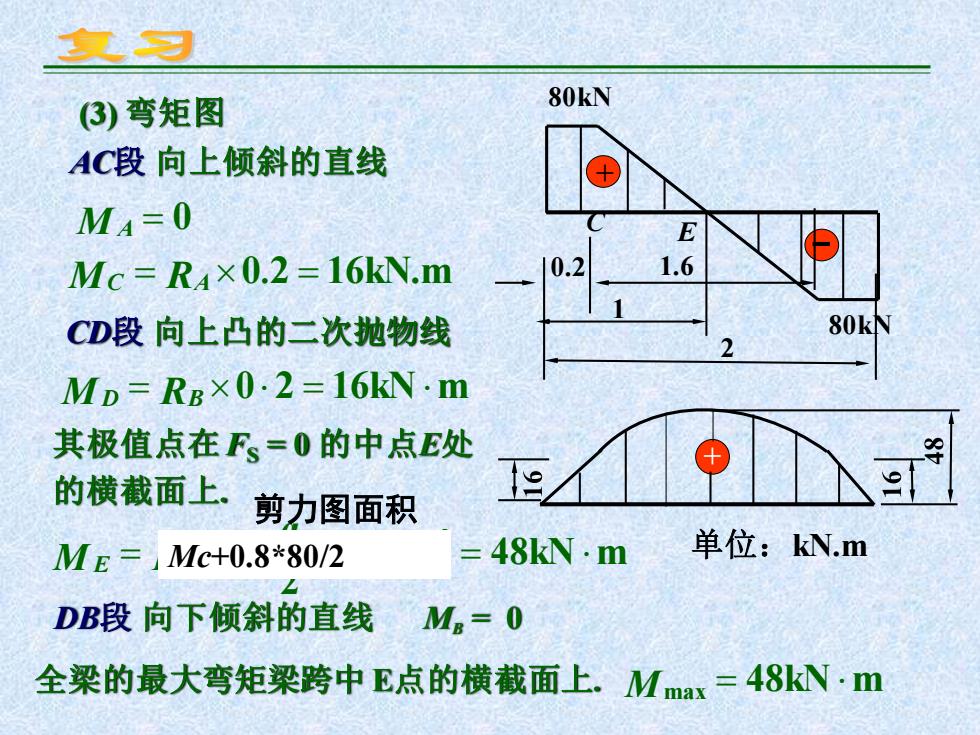
复习 3)弯矩图 80kN AC段向上倾斜的直线 M4=0 Mc=R4×0.2=16kN.m 0.2 1.6 CD段向上凸的二次抛物线 80k MD=Rε×0.2=16kNm 其极值点在F、=0的中点E处 的横截面上 9 剪力图面积 ME=Mc+0.8*80/2 =48kN·m 单位:kN.m DB段向下倾斜的直线 M=0 全梁的最大弯矩梁跨中E点的横截面上.Mmax=48kN,m
(3) 弯矩图 AC段 向上倾斜的直线 CD段 向上凸的二次抛物线 M A = 0 MC = RA 0.2 = 16kN.m MD = RB 0 2 = 16kN m 其极值点在FS = 0 的中点E处 的横截面上. (1 0 2) 48kN m 2 1 2 = − − = q ME RA DB段 向下倾斜的直线 MB = 0 + 单位:kN.m 全梁的最大弯矩梁跨中 E点的横截面上. Mmax = 48kN m Mc+0.8*80/2 + 80kN 80kN C 0.2 1.6 1 2 E 剪力图面积