
第10卷第4期 智能系统学报 Vol.10 No.4 2015年8月 CAAI Transactions on Intelligent Systems Feh.2015 D0:10.3969/j.issn.1673-4785.201403032 网s络出版地址:http:/www.cnki.net/kcms/detail/23.1538.TP.20150720.0911.002.html 基于改进逆向运动学的人体运动跟踪 赵军2,於俊2,汪增福23 (1.中国科学技术大学信息学院自动化系,安徽合肥230026:2.语音及语言信息处理国家工程实验室,安徽合肥 230026:3.中国科学院合肥智能机械研究所,安徽合肥230026) 摘要:随着人们对智能系统需求逐年增高,基于视觉的运动研究引起计算机视觉领域工作者更多的关注。这使它 成为模式识别、行为学、行为处理分析与处理等学科的研究热门。现存算法存在需要标记、相机标定等各种约束条 件,不能满足人们对人体运行跟踪的需求。论述了一种结合改进逆向运动学和图像模板匹配算法的人体运动位置 的跟踪方法。该算法以改进逆向运动学为框架,首先依据逆向运动学知识与正向运动学知识计算出的关节点的粗 略位置,对外观模型的各个模块进行模板匹配,接着确定关节点的最优位置,然后确定关节点的三维坐标值,最后重 构得到三维动作序列。实验表明,在主观视觉感受与客观衡量标准两方面,此算法获得的实验结果都能够逼近乃至 达到人体运动跟踪领域的最佳水准。 关键词:改进逆向运动学;基于视觉人体运动跟踪:模板匹配;计算机视觉;用户接口 中图分类号:TH186文献标志码:A文章编号:1673-4785(2015)04-0548-07 中文引用格式:赵军,於俊,汪增福.基于改进逆向运动学的人体运动跟踪[J].智能系统学报,2015,10(4):548-554. 英文引用格式:.ZHAO Jun,YUJun,WANG Zengfu..Human motion tracking based on an improved inverse kinematics[J】.CAAl Transactions on Intelligent Systems,2015,10(4):548-554. Human motion tracking based on an improved inverse kinematics ZHAO Jun'2,YU Jun'.2,WANG Zengfu'.2.3 (1.Department of Automation,University of Science and Technology of China,Hefei 230027,China;2.National Laboratory of Speech and Language Information Processing,Hefei 230027,China;3.Institute of Intelligent Machine,Chinese Academy of Sciences,Hefei 230027.China) Abstract:With the rising demand for intelligent systems,the study of vision-based human motion is drawing the machine vision investigators,making it become the research focus of pattern recognition,behavioral science,be- havior analyzing and processing.The existing algorithms have many kinds of restriction conditions,such as marking and camera calibration,not being able to meet people's demand for tracking human motion.Therefore,this article proposes a human motion position tracking algorithm on the basis of video,combining the template matching and improved inverse kinematics.It first calculates the coarse position of joint point according to the inverse kinematics and forward kinematics then applies template matching to each module of the appearing-model,and then deter- mines the optimal location of joints and the 3D coordinates of joints,and finally obtains the 3D action sequences by reconstruction.Experimental results show that this algorithm can be close to and even reach the best level in both subjective visual feel and objective weighing standard in the field of human motion tracking. Keywords:improved inverse kinematics;human motion tracking;template matching;computer vision;user inter- face 随着日渐成熟的计算机水平的发展,根据视觉 领域的研究。 的人体的运动跟踪和运动剖析逐渐成为当今计算机 本文在综合考虑跟踪效果和计算效率的情况 视觉学科的科研热门,同时人机交互、基于运动的识 下,提出了一种简单高效、且不牺牲跟踪结果质量的 别、虚拟现实等有关领域[]的迫切需求也推动此 基于棍状模型的算法。 方向的飞速进展,推动了大量的研究人员加入这个 1)本文对基于逆向运动跟踪算法的关节位置 预测方法和旋转角计算方法进行了改进。关节位置 收稿日期:2014-03-12.网络出版日期:2015-07-20 预测方法的优劣会影响跟踪算法效率和有效性。基 基金项目:国家自然科学基金资助项目(61303150) 通信作者:赵军.E-mail:zhuyihangl123@hotmail.com. 于逆向运动跟踪算法做了关节的运行模式是速度不
第 10 卷第 4 期 智 能 系 统 学 报 Vol.10 №.4 2015 年 8 月 CAAI Transactions on Intelligent Systems Feb. 2015 DOI:10.3969 / j.issn.1673⁃4785.201403032 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20150720.0911.002.html 基于改进逆向运动学的人体运动跟踪 赵军1,2 , 於俊1,2 ,汪增福1,2,3 (1.中国科学技术大学 信息学院自动化系,安徽 合肥 230026;2.语音及语言信息处理国家工程实验室,安徽 合肥 230026;3.中国科学院 合肥智能机械研究所,安徽 合肥 230026) 摘 要:随着人们对智能系统需求逐年增高,基于视觉的运动研究引起计算机视觉领域工作者更多的关注。 这使它 成为 模式识别、行为学、行为处理分析与处理等学科的研究热门。 现存算法存在需要标记、相机标定等各种约束条 件,不能满足人们对人体运行跟踪的需求。 论述了一种结合改进逆向运动学和图像模板匹配算法的人体运动位置 的跟踪方法。 该算法以改进逆向运动学为框架,首先依据逆向运动学知识与正向运动学知识计算出的关节点的粗 略位置,对外观模型的各个模块进行模板匹配,接着确定关节点的最优位置,然后确定关节点的三维坐标值,最后重 构得到三维动作序列。 实验表明,在主观视觉感受与客观衡量标准两方面,此算法获得的实验结果都能够逼近乃至 达到人体运动跟踪领域的最佳水准。 关键词:改进逆向运动学;基于视觉人体运动跟踪;模板匹配;计算机视觉;用户接口 中图分类号:TH186 文献标志码:A 文章编号:1673⁃4785(2015)04⁃0548⁃07 中文引用格式:赵军,於俊,汪增福.基于改进逆向运动学的人体运动跟踪[J]. 智能系统学报, 2015, 10(4): 548⁃554. 英文引用格式:.ZHAO Jun, YU Jun, WANG Zengfu.Human motion tracking based on an improved inverse kinematics [J]. CAAI Transactions on Intelligent Systems, 2015, 10(4): 548⁃554. Human motion tracking based on an improved inverse kinematics ZHAO Jun 1, 2 , YU Jun 1, 2 , WANG Zengfu 1, 2, 3 (1. Department of Automation, University of Science and Technology of China, Hefei 230027, China; 2. National Laboratory of Speech and Language Information Processing, Hefei 230027, China; 3. Institute of Intelligent Machine, Chinese Academy of Sciences, Hefei 230027, China) Abstract:With the rising demand for intelligent systems, the study of vision⁃based human motion is drawing the machine vision investigators, making it become the research focus of pattern recognition, behavioral science, be⁃ havior analyzing and processing. The existing algorithms have many kinds of restriction conditions, such as marking and camera calibration, not being able to meet people's demand for tracking human motion. Therefore, this article proposes a human motion position tracking algorithm on the basis of video, combining the template matching and improved inverse kinematics. It first calculates the coarse position of joint point according to the inverse kinematics and forward kinematics , then applies template matching to each module of the appearing⁃model, and then deter⁃ mines the optimal location of joints and the 3D coordinates of joints, and finally obtains the 3D action sequences by reconstruction. Experimental results show that this algorithm can be close to and even reach the best level in both subjective visual feel and objective weighing standard in the field of human motion tracking. Keywords:improved inverse kinematics; human motion tracking; template matching; computer vision; user inter⁃ face 收稿日期:2014⁃03⁃12. 网络出版日期:2015⁃07⁃20. 基金项目:国家自然科学基金资助项目(61303150). 通信作者:赵军. E⁃mail:zhuyihang1123@ hotmail.com. 随着日渐成熟的计算机水平的发展,根据视觉 的人体的运动跟踪和运动剖析逐渐成为当今计算机 视觉学科的科研热门,同时人机交互、基于运动的识 别、虚拟现实等有关领域[1⁃2] 的迫切需求也推动此 方向的飞速进展,推动了大量的研究人员加入这个 领域的研究。 本文在综合考虑跟踪效果和计算效率的情况 下,提出了一种简单高效、且不牺牲跟踪结果质量的 基于棍状模型的算法。 1)本文对基于逆向运动跟踪算法的关节位置 预测方法和旋转角计算方法进行了改进。 关节位置 预测方法的优劣会影响跟踪算法效率和有效性。 基 于逆向运动跟踪算法做了关节的运行模式是速度不

第4期 赵军,等:基于改进逆向运动学的人体运动跟踪 ·549. 变的假设,而真实的跟踪过程中关节运动模型是变 2)人体外观模型。人体外观模型由外观形状 速且带有随机性的,会导致局部寻优较慢:当预测位 模型及外观纹理模型构成。如图2所示,人体外观 置出现较大偏差,关节不在寻优区域时,会导致找不 模型共由一些矩形块构成。每个矩形对应人体的一 到准确的关节位置。因此,采用了粒子滤波的方式 节身体片段。矩形由人体段内部的像素值构成,其 对关节位置进行预测,提高了跟踪的有效性。 中相对坐标是形状模型及像素值是纹理模型。 2)文中同时提出了利用3dmax生成序列图片 作为测试样本,将跟踪结果与3dmax得到的真实数 据进行比较的验证方法。其中,图片序列的生成过 程采用根据已知运动目标的关节位置,生成人体的 动作序列,进而生成实验所需视频。然后,使用传统 算法与本文算法在生成所得视频基础上进行运动目 标的跟踪,从而获得运动目标的最优估计值。最后 将估计值与原始的真实值比较,通过计算人体各关 节图像空间的像素值偏差,说明本文算法的有效性。 1人体骨骼及外观模型 图2人体外观模型 Fig.2 Rep of human body's appearance model 本节介绍本文所用的人体骨骼模型和人体外观 3)摄像机成像模型。三维空间中某点的坐标 模型及对相关名称进行解释。 值与该点在二维投影平面上的坐标(,)满足以 1)人体骨骼模型如图1所示。本文将人体看 下方程: 成是一种棍状树型模型,其包含15节身体片与8对 关节。其中,根节点J1对应人体骨骼结构的盆骨: 10 (1) J:对应的人体位置,如图1所示。文中在人体骨骼 01 模型上定义了2种坐标系:(a)局部坐标系,坐标系 的原点为相应关节,坐标系方向,如图2右上方所 参数:是反比例因子,根据公式:=子计算得 示:(b)基坐标系。此坐标系的中心点为J1关节。 到6。此公式中,∫是相机的焦距,:是此点的相机 它的轴向与系统开始状态下J,局部坐标系的轴向 透视空间深度坐标。从式(1)可知,△s=T(4z),即 保持相同。文中用欧拉角[来标识关节的旋转,它 △s与Az成正比例。 的公式是(α,B,y),其中a表示绕x轴旋转角度,B 表示绕y轴旋转角度,y表示绕z轴旋转角度。 2算法框架 不失一般性,本文讨论人身体各个关节运动的 问题。本文算法框图如图3所示,包含下面4步。 1)跟踪系统初始化。使用者根据跟踪系统提 z坐标正方向指向纸背 供的输入界面来确定人体骨骼模型和外观模型。如 图4,外观模型是人体各段的像素信息。该部分输 入为视频第一帧图像,由使用者在其上标识出的关 节点位置计算出人体外观模型及人体骨架模型[) 中各身体部分的相对尺寸。 2)求旋转欧拉角。按照树形化方式[8],如图1 右图。由待计算关节的预测的在二维图像中的位 置,借助逆向运动学模型计算出此关节所在人体片 段的旋转角度。第一步依据人体各部分相对比值计 算出此关节在透视相机模型下相应的立体空间坐 右 标。第2步根据改进的逆向运动学计算出旋转角。 图1人体骨骼和关节模型 3)求关节在图像中的位置。根据上一步获得 Fig.1 The human bone model and joint model 的关节旋转欧拉角依照正向运动学劉计算出此关
变的假设,而真实的跟踪过程中关节运动模型是变 速且带有随机性的,会导致局部寻优较慢;当预测位 置出现较大偏差,关节不在寻优区域时,会导致找不 到准确的关节位置。 因此,采用了粒子滤波的方式 对关节位置进行预测,提高了跟踪的有效性。 2)文中同时提出了利用 3dmax 生成序列图片 作为测试样本,将跟踪结果与 3dmax 得到的真实数 据进行比较的验证方法。 其中,图片序列的生成过 程采用根据已知运动目标的关节位置,生成人体的 动作序列,进而生成实验所需视频。 然后,使用传统 算法与本文算法在生成所得视频基础上进行运动目 标的跟踪,从而获得运动目标的最优估计值。 最后 将估计值与原始的真实值比较,通过计算人体各关 节图像空间的像素值偏差,说明本文算法的有效性。 1 人体骨骼及外观模型 本节介绍本文所用的人体骨骼模型和人体外观 模型及对相关名称进行解释。 1)人体骨骼模型如图 1 所示。 本文将人体看 成是一种棍状树型模型,其包含 15 节身体片与 8 对 关节。 其中,根节点 J1 对应人体骨骼结构的盆骨; Ji 对应的人体位置,如图 1 所示。 文中在人体骨骼 模型上定义了 2 种坐标系:( a)局部坐标系,坐标系 的原点为相应关节,坐标系方向,如图 2 右上方所 示;(b)基坐标系。 此坐标系的中心点为 J1 关节。 它的轴向与系统开始状态下 J1 局部坐标系的轴向 保持相同。 文中用欧拉角[15]来标识关节的旋转,它 的公式是 (α,β,γ) ,其中 α 表示绕 x 轴旋转角度, β 表示绕 y 轴旋转角度, γ 表示绕 z 轴旋转角度。 图 1 人体骨骼和关节模型 Fig.1 The human bone model and joint model 2)人体外观模型。 人体外观模型由外观形状 模型及外观纹理模型构成。 如图 2 所示,人体外观 模型共由一些矩形块构成。 每个矩形对应人体的一 节身体片段。 矩形由人体段内部的像素值构成,其 中相对坐标是形状模型及像素值是纹理模型。 图 2 人体外观模型 Fig.2 Rep of human body’s appearance model 3)摄像机成像模型。 三维空间中某点的坐标 值与该点在二维投影平面上的坐标 (u,v) 满足以 下方程: u v æ è ç ö ø ÷ = 1 s 1 0 0 0 0 1 æ è ç ö ø ÷ x y z æ è ç ç ç ö ø ÷ ÷ ÷ (1) 参数 s 是反比例因子,根据公式 s = z f 计算得 到[16] 。 此公式中, f 是相机的焦距, z 是此点的相机 透视空间深度坐标。 从式(1)可知, Δs = T(Δz) ,即 Δs 与 Δz 成正比例。 2 算法框架 不失一般性,本文讨论人身体各个关节运动的 问题。 本文算法框图如图 3 所示,包含下面 4 步。 1)跟踪系统初始化。 使用者根据跟踪系统提 供的输入界面来确定人体骨骼模型和外观模型。 如 图 4,外观模型是人体各段的像素信息。 该部分输 入为视频第一帧图像,由使用者在其上标识出的关 节点位置计算出人体外观模型及人体骨架模型[17] 中各身体部分的相对尺寸。 2)求旋转欧拉角。 按照树形化方式[18] ,如图 1 右图。 由待计算关节的预测的在二维图像中的位 置,借助逆向运动学模型计算出此关节所在人体片 段的旋转角度。 第一步依据人体各部分相对比值计 算出此关节在透视相机模型下相应的立体空间坐 标。 第 2 步根据改进的逆向运动学计算出旋转角。 3)求关节在图像中的位置。 根据上一步获得 的关节旋转欧拉角依照正向运动学[8] 计算出此关 第 4 期 赵军,等:基于改进逆向运动学的人体运动跟踪 ·549·
.550 智能系统学报 第10卷 节所在的人体片段中所有像素旋转后的立体坐标 值时,我们把相应的关节位置当做计算出的最准确 值。最后根据摄像机投影模型把人体片段投影到二 的关节位置。同时,此时由所有人体关节位置重构 维平面。从而计算出待计算的关节点相应的人体片 的人体形态为实验最准确的形态。 段在二维平面上的坐标值。因此,获得形变身体段。 本文不对步骤1)~4)进行详细叙述,如有需要 4)直方图匹配。将形变身体段与系统初始化 请参考邹北骥[4的相关文章。 时得到的外观模型做直方图匹配。在相似度为极大 输出相似度 最大值所对 应的欧拉角 正运行学求的对 外观模型 模板匹配 应骨骼段像素在当慚 图像上的坐植值 旋转欧拉角十 关节在图像 关节点手 局部搜索进行 逆向运动学求 上的二维 得该关节的旋转 工标注 坐标值 关系节匹配 待匹配 欧拉角 关节 人体骨骼 坐标 比例 摄像机成像 模型求解 图3算法框架图 Fig.3 Diagram of the ALG framework cos a sin a 0 R= sin a cos a 0 0 cos B 0 sin B7[1 0 0 0 1 0 0 cos y -sin y (2) L-sin B 0 cos B0 sin y cos y 如图5所示,在三维空间中,可以知道旋转可以 通过3个欧拉角(α,B,y)来定义,欧拉旋转定理表 明,任意2个具有相同原点的三维空间坐标系变换, 可以通过绕一包含原,点的固定轴进行相应旋转来实 现。这里的转动参量是由旋转角度和那条固定的旋 转轴(即欧拉角和欧拉轴)来表示的。 图4标注后的视频首帧 如图6所示,三维空间中有一初始矢量为 Fig.4 The video's Fst-frame after annotation r(OP),绕欧拉轴转动后变为r',n为欧拉轴的单位 3算法改进 向量,p表示r(OP)到'(OQ)的旋转角,n与p的 求解方式是2个向量的叉乘为欧拉轴,点乘为旋转角 3.1计算旋转角方法的改进 的余弦。具体求解公式为 逆向运动学算法计算旋转欧拉角的方法,其假定 P·r 当J,∈{J4,J,Jo,J}时,绕y轴旋转分量α=0:否 n=nor(r×r'),cosp=rl可 (3) 则,绕x轴旋转分量B=0:即必须加上绕y轴或者绕其中,or()表示向量归一化。 x轴旋转分量为零的约束。在跟踪过程中,人体的主 现在由欧拉轴和旋转角,求得其对应的四元数, 要关节或多或少都会沿某个轴向发生旋转,上述约束设n=(m1,n2,),则四元数计算公式为 是不符合真实情况的,所以计算出的旋转角是有误差 q=[sin(p/2)×n1,sin(p/2)×n2, 的。基于此缺陷本文找到了一种精确计算旋转角的 sin(o/2)x ns,cos(/2)] (4) 方法[ 接下来由四元数求得欧拉角,设q= [x,y,z,w],欧拉角0=(a,B,Y),则欧拉角的计算
节所在的人体片段中所有像素旋转后的立体坐标 值。 最后根据摄像机投影模型把人体片段投影到二 维平面。 从而计算出待计算的关节点相应的人体片 段在二维平面上的坐标值。 因此,获得形变身体段。 4)直方图匹配。 将形变身体段与系统初始化 时得到的外观模型做直方图匹配。 在相似度为极大 值时,我们把相应的关节位置当做计算出的最准确 的关节位置。 同时,此时由所有人体关节位置重构 的人体形态为实验最准确的形态。 本文不对步骤 1) ~4)进行详细叙述,如有需要 请参考邹北骥[14]的相关文章。 图 3 算法框架图 Fig.3 Diagram of the ALG framework 图 4 标注后的视频首帧 Fig.4 The video’s Fst⁃frame after annotation 3 算法改进 3.1 计算旋转角方法的改进 逆向运动学算法计算旋转欧拉角的方法,其假定 当 Ji ∈ J4 ,J7 ,J10 ,J13 { } 时,绕 y 轴旋转分量 α = 0;否 则,绕 x 轴旋转分量 β = 0;即必须加上绕 y 轴或者绕 x 轴旋转分量为零的约束。 在跟踪过程中,人体的主 要关节或多或少都会沿某个轴向发生旋转,上述约束 是不符合真实情况的,所以计算出的旋转角是有误差 的。 基于此缺陷本文找到了一种精确计算旋转角的 方法[9] 。 i-1 i R = cos α - sin α 0 sin α cos α 0 0 0 1 é ë ê ê ê ù û ú ú ú cos β 0 sin β 0 1 0 - sin β 0 cos β é ë ê ê ê ù û ú ú ú 1 0 0 0 cos γ - sin γ 0 sin γ cos γ é ë ê ê ê ù û ú ú ú (2) 如图 5 所示,在三维空间中,可以知道旋转可以 通过 3 个欧拉角 (α,β,γ) 来定义,欧拉旋转定理表 明,任意 2 个具有相同原点的三维空间坐标系变换, 可以通过绕一包含原点的固定轴进行相应旋转来实 现。 这里的转动参量是由旋转角度和那条固定的旋 转轴(即欧拉角和欧拉轴)来表示的。 如图 6 所 示, 三 维 空 间 中 有 一 初 始 矢 量 为 r(OP) ,绕欧拉轴转动后变为 r′,n 为欧拉轴的单位 向量, φ 表示 r(OP) 到 r′ → (OQ) 的旋转角, n 与 φ 的 求解方式是 2 个向量的叉乘为欧拉轴,点乘为旋转角 的余弦。 具体求解公式为 n = nor(r × r′),cosφ = r·r′ r r′ (3) 其中,nor()表示向量归一化。 现在由欧拉轴和旋转角,求得其对应的四元数, 设 n = (n1 ,n2 ,n3 ) ,则四元数计算公式为 q = [sin(φ/ 2) × n1 ,sin(φ/ 2) × n2 , sin(φ/ 2) × n3 ,cos(φ/ 2) ] (4) 接 下 来 由 四 元 数 求 得 欧 拉 角, 设 q = [x,y,z,w] ,欧拉角 o = (α,β,γ) ,则欧拉角的计算 ·550· 智 能 系 统 学 报 第 10 卷

第4期 赵军,等:基于改进逆向运动学的人体运动跟踪 ·551. 公式为 较慢,即迭代次数会变多;当预测位置出现较大偏差 2(q293+9o91) 时,关节位置不在寻优区域导致找不到准确位置,会 a arctan(- 6-9-92+9后 将错误的位置当做关节位置,进而影响算法后面的部 arctan(-2(q193-9o92) 分,导致错误的跟踪。因此,本文采用了粒子滤波的 2(9192+9093) 方式[3]对关节位置进行预测。 y=acan(6+i-i-g 下面只对粒子滤波的自回归过程进行介绍,其他 部分请参考文献[13]。自回归过程是一种通过历史 数据来预测目前状态的时间序列建模策略。在这个 模型里,目前的状态x,是一个依赖于以前状态的确 定性函数并加上随机干扰,假如确定性函数是线性 的,则目前的状态依赖于以前的x。个状态,模型可以 写成 气=龙4+@ (7) i=1 {a:}-1是自回归系数;w,是随机干扰,一般情 况下是白噪声。自回归系数既可通过学习的方法得 图5欧拉角示意图 到,也可以由特别的方式指定6。由于跟踪目标 Fig.5 Euler Angle diagram 的连续性,采用变速模型更为适合一些,这里采用三 阶自回归模型: x=Ax-1+Bx-2+Cx-3+DN(0,∑)(8) 式中:{4,B,C,D}=1是自回归系数,N(O,∑)是 零均值、标准方差为1的Gaussian噪声。在试验中, 指定系数为A=2,B=-2,C=3,D=1。 由上述计算过程可知,文中引入了变速模型和噪 声,变速模型相对匀速模型能够更准确地表示关节的 运动模型:引入噪声符合关节的运动具有随机性的特 性,即关节有时会发生微小抖动。 因此,本文方法相对基于逆向运动学的方法能够 更加准确地表示运动模型,进而能够更加有效的预测 图6欧拉轴和旋转角示意图 关节的位置,从而为后续的局部寻优,提供一个有效 Fig.6 Euler axis and rotation Angle 的预测,进而更加迅速和准确地找到最优估计,同时 由上述计算过程可以看出,本文采用的计算旋转角的 也会减少准确位置在寻优区域外部的概率,最终能够 方法是准确值,包括αB、y等3个旋转分量,所以能 够获得比通过逆向运动学计算更加准确的旋转角。与分析部分。 提高跟踪的速度和有效性。具体结果参见实验结果 因此,最后的跟踪效果能够比基于逆向运动学的效果 3.3实验准则的改进 要好,具体结果参见实验结果与分析部分。 基于逆向运动学的实验准则,即通过手工标注的 3.2关节位置预测方法的改进 方式。手工标注的方式是通过人工标记获得实验图 计算旋转角的方法中有一步是预测关节在图像 片序列中运动目标关节的二维图像位置,通过这种方 中的位置,其利用X-1=[x,-1y-]T,X-2= 式获取的关节位置具有主观性,因此获得的关节位置 [x,-2水-2】T即在1-1与t-2时刻的最优估计位置 只能近似为真实的关节位置。 计算出V,-1=[x-1-x-2y-1-y-2]T关节在t-1 基于手工标注的主观性,提出了模拟仿真的方 时刻的速度,然后估计关节在t~1时刻的位置X,=式。模拟仿真的方式是通过某种方式根据运动目标 [x,少,]「。可以发现,该算法做了关节的运行模式是的关节位置,生成相应的图片序列并将其作为测试视 速度不变的假设,而真实的跟踪过程中关节的运动模频。此种方式获得的真实关节位置是相当可靠和准 型是变速的且带有随机性的,会导致他们的局部寻优确的。具体方法是测试图像序列由3DMax软件生
公式为 α = arctan( 2(q2 q3 + q0 q1 ) q 2 0 - q 2 1 - q 2 2 + q 2 3 ) = arctan( - 2(q1 q3 - q0 q2 )) γ = arctan( 2(q1 q2 + q0 q3 ) q 2 0 + q 2 1 - q 2 2 - q 2 3 ) 图 5 欧拉角示意图 Fig.5 Euler Angle diagram 图 6 欧拉轴和旋转角示意图 Fig.6 Euler axis and rotation Angle 由上述计算过程可以看出,本文采用的计算旋转角的 方法是准确值,包括 α、β、γ 等 3 个旋转分量,所以能 够获得比通过逆向运动学计算更加准确的旋转角。 因此,最后的跟踪效果能够比基于逆向运动学的效果 要好,具体结果参见实验结果与分析部分。 3.2 关节位置预测方法的改进 计算旋转角的方法中有一步是预测关节在图像 中 的 位 置, 其 利 用 Xt-1 = xt-1 ,yt-1 [ ] T ,Xt-2 = xt-2 ,yt-2 [ ] T 即在 t - 1 与 t - 2 时刻的最 优估计位置 计算出 Vt-1 = xt-1 - xt-2 ,yt-1 - yt-2 [ ] T 关节在 t -1 时刻的速度,然后估计关节在 t-1 时刻的位置 Xt = xt,yt [ ] T 。 可以发现,该算法做了关节的运行模式是 速度不变的假设,而真实的跟踪过程中关节的运动模 型是变速的且带有随机性的,会导致他们的局部寻优 较慢,即迭代次数会变多;当预测位置出现较大偏差 时,关节位置不在寻优区域导致找不到准确位置,会 将错误的位置当做关节位置,进而影响算法后面的部 分,导致错误的跟踪。 因此,本文采用了粒子滤波的 方式[13]对关节位置进行预测。 下面只对粒子滤波的自回归过程进行介绍,其他 部分请参考文献[13]。 自回归过程是一种通过历史 数据来预测目前状态的时间序列建模策略。 在这个 模型里,目前的状态 xt 是一个依赖于以前状态的确 定性函数并加上随机干扰,假如确定性函数是线性 的,则目前的状态依赖于以前的 xp 个状态,模型可以 写成 xt = ∑ p i = 1 ∂i xt-i + ωt (7) ∂i { } p i = 1 是自回归系数; ωt 是随机干扰,一般情 况下是白噪声。 自回归系数既可通过学习的方法得 到[15] ,也可以由特别的方式指定[16] 。 由于跟踪目标 的连续性,采用变速模型更为适合一些,这里采用三 阶自回归模型: xt = Axt-1 + Bxt-2 + Cxt-3 + DN(0,∑) (8) 式中: {A,B,C,D} p i = 1 是自回归系数, N(0,∑) 是 零均值、标准方差为 1 的 Gaussian 噪声。 在试验中, 指定系数为 A = 2,B = - 2,C = 3,D= 1。 由上述计算过程可知,文中引入了变速模型和噪 声,变速模型相对匀速模型能够更准确地表示关节的 运动模型;引入噪声符合关节的运动具有随机性的特 性,即关节有时会发生微小抖动。 因此,本文方法相对基于逆向运动学的方法能够 更加准确地表示运动模型,进而能够更加有效的预测 关节的位置,从而为后续的局部寻优,提供一个有效 的预测,进而更加迅速和准确地找到最优估计,同时 也会减少准确位置在寻优区域外部的概率,最终能够 提高跟踪的速度和有效性。 具体结果参见实验结果 与分析部分。 3.3 实验准则的改进 基于逆向运动学的实验准则,即通过手工标注的 方式。 手工标注的方式是通过人工标记获得实验图 片序列中运动目标关节的二维图像位置,通过这种方 式获取的关节位置具有主观性,因此获得的关节位置 只能近似为真实的关节位置。 基于手工标注的主观性,提出了模拟仿真的方 式。 模拟仿真的方式是通过某种方式根据运动目标 的关节位置,生成相应的图片序列并将其作为测试视 频。 此种方式获得的真实关节位置是相当可靠和准 确的。 具体方法是测试图像序列由 3DMax 软件生 第 4 期 赵军,等:基于改进逆向运动学的人体运动跟踪 ·551·
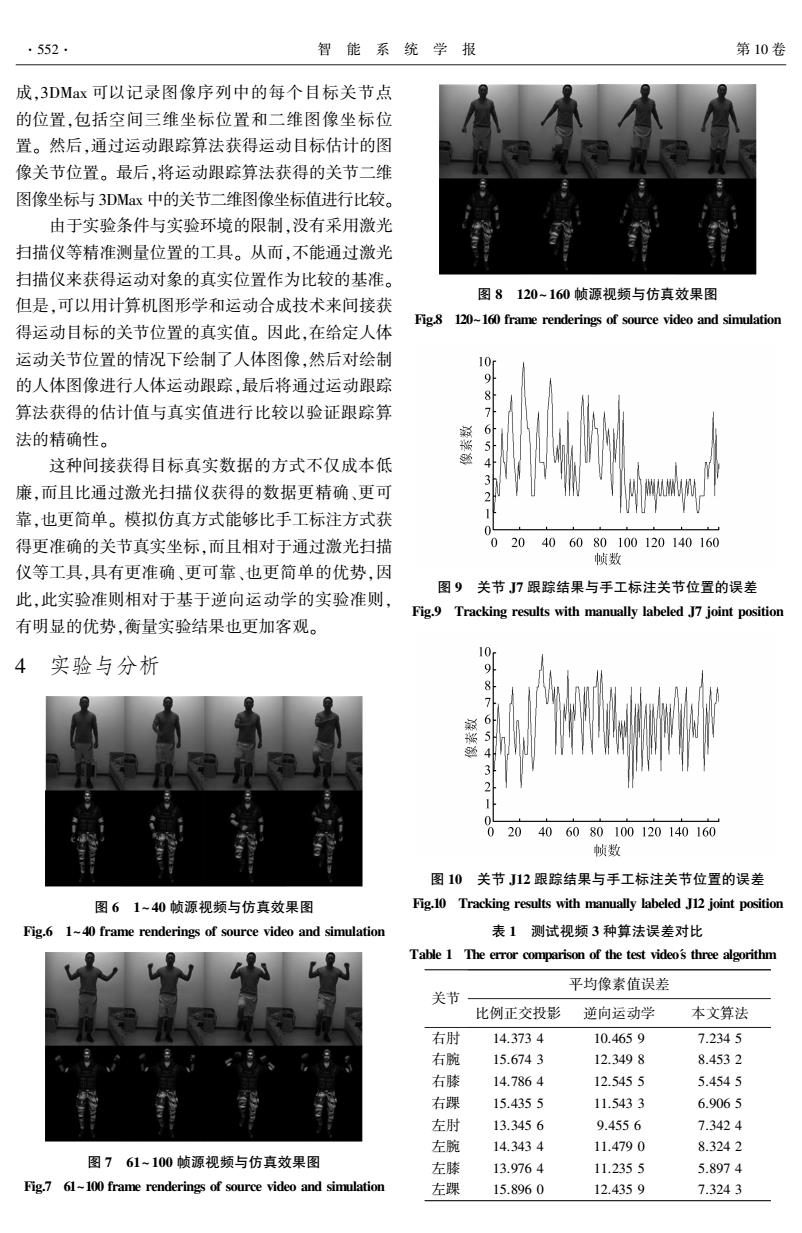
.552. 智能系统学报 第10卷 成,3DMax可以记录图像序列中的每个目标关节点 的位置,包括空间三维坐标位置和二维图像坐标位 置。然后,通过运动跟踪算法获得运动目标估计的图 像关节位置。最后,将运动跟踪算法获得的关节二维 图像坐标与3DMax中的关节二维图像坐标值进行比较。 由于实验条件与实验环境的限制,没有采用激光 扫描仪等精准测量位置的工具。从而,不能通过激光 扫描仪来获得运动对象的真实位置作为比较的基准。 图8120-160帧源视频与仿真效果图 但是,可以用计算机图形学和运动合成技术来间接获 Fig.8 120-160 frame renderings of source video and simulation 得运动目标的关节位置的真实值。因此,在给定人体 运动关节位置的情况下绘制了人体图像,然后对绘制 10m 的人体图像进行人体运动跟踪,最后将通过运动跟踪 算法获得的估计值与真实值进行比较以验证跟踪算 987 法的精确性。 6 这种间接获得目标真实数据的方式不仅成本低 廉,而且比通过激光扫描仪获得的数据更精确、更可 2 靠,也更简单。模拟仿真方式能够比手工标注方式获 得更准确的关节真实坐标,而且相对于通过激光扫描 02040 6080100120140160 帧数 仪等工具,具有更准确、更可靠、也更简单的优势,因 图9关节J7跟踪结果与手工标注关节位置的误差 此,此实验准则相对于基于逆向运动学的实验准则, Fig.9 Tracking results with manually labeled J7 joint position 有明显的优势,衡量实验结果也更加客观。 10 4实验与分析 9 8 6 5 4 0 020406080100120140160 帧数 图10关节J12跟踪结果与手工标注关节位置的误差 图61~40帧源视频与仿真效果图 Fig.10 Tracking results with manually labeled J12 joint position Fig.6 1~40 frame renderings of source video and simulation 表1测试视频3种算法误差对比 Table 1 The error comparison of the test video's three algorithm 平均像素值误差 关节 比例正交投影 逆向运动学 本文算法 右肘 14.3734 10.4659 7.2345 右腕 15.6743 12.3498 8.4532 右膝 14.7864 12.5455 5.4545 右踝 15.4355 11.5433 6.9065 左肘 13.3456 9.4556 7.3424 左腕 14.3434 11.4790 8.3242 图761~100帧源视频与仿真效果图 左膝 13.9764 11.2355 5.8974 Fig.7 61~100 frame renderings of source video and simulation 左踝 15.8960 12.4359 7.3243
成,3DMax 可以记录图像序列中的每个目标关节点 的位置,包括空间三维坐标位置和二维图像坐标位 置。 然后,通过运动跟踪算法获得运动目标估计的图 像关节位置。 最后,将运动跟踪算法获得的关节二维 图像坐标与 3DMax 中的关节二维图像坐标值进行比较。 由于实验条件与实验环境的限制,没有采用激光 扫描仪等精准测量位置的工具。 从而,不能通过激光 扫描仪来获得运动对象的真实位置作为比较的基准。 但是,可以用计算机图形学和运动合成技术来间接获 得运动目标的关节位置的真实值。 因此,在给定人体 运动关节位置的情况下绘制了人体图像,然后对绘制 的人体图像进行人体运动跟踪,最后将通过运动跟踪 算法获得的估计值与真实值进行比较以验证跟踪算 法的精确性。 这种间接获得目标真实数据的方式不仅成本低 廉,而且比通过激光扫描仪获得的数据更精确、更可 靠,也更简单。 模拟仿真方式能够比手工标注方式获 得更准确的关节真实坐标,而且相对于通过激光扫描 仪等工具,具有更准确、更可靠、也更简单的优势,因 此,此实验准则相对于基于逆向运动学的实验准则, 有明显的优势,衡量实验结果也更加客观。 4 实验与分析 图 6 1~ 40 帧源视频与仿真效果图 Fig.6 1~40 frame renderings of source video and simulation 图 7 61~ 100 帧源视频与仿真效果图 Fig.7 61~100 frame renderings of source video and simulation 图 8 120~ 160 帧源视频与仿真效果图 Fig.8 120~160 frame renderings of source video and simulation 图 9 关节 J7 跟踪结果与手工标注关节位置的误差 Fig.9 Tracking results with manually labeled J7 joint position 图 10 关节 J12 跟踪结果与手工标注关节位置的误差 Fig.10 Tracking results with manually labeled J12 joint position 表 1 测试视频 3 种算法误差对比 Table 1 The error comparison of the test video's three algorithm 关节 平均像素值误差 比例正交投影 逆向运动学 本文算法 右肘 14.373 4 10.465 9 7.234 5 右腕 15.674 3 12.349 8 8.453 2 右膝 14.786 4 12.545 5 5.454 5 右踝 15.435 5 11.543 3 6.906 5 左肘 13.345 6 9.455 6 7.342 4 左腕 14.343 4 11.479 0 8.324 2 左膝 13.976 4 11.235 5 5.897 4 左踝 15.896 0 12.435 9 7.324 3 ·552· 智 能 系 统 学 报 第 10 卷