
第10卷第4期 智能系统学报 Vol.10 No.4 2015年8月 CAAI Transactions on Intelligent Systems Aug.2015 D0:10.3969/j.issn.1673-4785.201503039 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20150702.1104.001.html 人体下肢生物力学建模研究进展 邵明旭,王斐,般腾龙,刘健 (东北大学信息科学与工程学院,辽宁沈阳110819) 摘要:人体下肢生物力学建模与仿真是穿戴式外骨骼机器人系统开发的一个重要内容。对其研究所获得相关的 理论与技术方法对生物动力学、康复医学、假肢及运动康复器械设计等领域的发展具有促进作用。本文以人体下肢 生物力系统为研究对象,概括和总结了国内外下肢建模与仿真技术的研究现状,就目前普遍采用的基于Lagrange方 程和角动量定理的多刚体模型法、仿真软件建模法、H三元素法、黑箱训练等方法进行了详细的分析,并对研究趋 势进行了展望。本文所综述的动力学建模与仿真验证方法对实现穿戴式外骨骼机器人和谐自然人机交互设计具有 重要的指导意义。 关键词:下肢生物力学建模;Lagrange方程;角动量定理;Hill模型;仿真软件建模;黑箱训练法 中图分类号:TP391文献标志码:A文章编号:1673-4785(2015)04-0518-10 中文引用格式:邵明旭,王斐,殷腾龙,等.人体下肢生物力学建模研究进展[J].智能系统学报,2015,10(4):518-527. 英文引用格式:SHAO Mingxu,WANG Fei,YIN Tenglong,etal.Progress on the research of human lower limb biomechanical modeling[J].CAAI Transactions on Intelligent Systems,2015,10(4):518-527. Research progress on the human lower limb biomechanical modeling SHAO Mingxu,WANG Fei,YIN Tenglong,LIU Jian (College of Information Science and Engineering,Northeastern University,Shenyang 110819,China) Abstract:The research on the biomechanical modeling and simulation of human lower limbs is an important content in the development of wearable exoskeleton robots.Theoretical and technical methods derived from this research can promote the process of biomechanics,rehabilitation medicine and prosthetic/orthotic devices.This work reviews the state-of-the-art techniques for modeling and simulating biomechanics of human lower limbs and makes analysis of popular methods,such as multi-body modeling,simulation software modeling,Hill three elements modeling and black box training modeling based on Lagrange equation and theorem of angular momentum.The future prospects in this research field are also provided in this paper.The biomechanical modeling and simulating methods discussed is of great significance to the design of naturally harmonious human-robot interaction of wearable exoskeleton robots. Keywords:biomechanical modeling of human lower limb;Lagrange equation;theorem of angular momentum;Hill model;simulation software modeling;black box training modeling 随着MEMS、材料、控制和计算机技术的飞速发围内引起了越来越多学者的关注。但目前的动力外 展,以及我国快速进入老龄化社会后对康复辅助设 骨骼和假肢研究存在的一个共性问题是对人体感觉 备的旺盛需求,穿戴式外骨骼机器人技术在世界范 运动控制、生物力学等知识了解不够,这就导致了 虽然设计出了先进的机器人硬件和软件,但由于没 收稿日期:2015-03-24.网络出版日期:2015-07-02 有考虑人如何作用,因此设备在与人交互和协同方 基金项目:中央高校基础科研业务费资助项目(120124002):辽宁省自 面效果欠佳。由于人体结构和功能的特殊性和复杂 然科学基金资助项目(2013020040). 通信作者:王斐.E-mail:wangfei@(ise.ncu.cd.cn 性,建立一个能完全反映人体状态的生物力学模型
第 10 卷第 4 期 智 能 系 统 学 报 Vol.10 №.4 2015 年 8 月 CAAI Transactions on Intelligent Systems Aug. 2015 DOI:10.3969 / j.issn.1673⁃4785.201503039 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150702.1104.001.html 人体下肢生物力学建模研究进展 邵明旭,王斐,殷腾龙,刘健 (东北大学 信息科学与工程学院,辽宁 沈阳 110819) 摘 要:人体下肢生物力学建模与仿真是穿戴式外骨骼机器人系统开发的一个重要内容。 对其研究所获得相关的 理论与技术方法对生物动力学、康复医学、假肢及运动康复器械设计等领域的发展具有促进作用。 本文以人体下肢 生物力系统为研究对象,概括和总结了国内外下肢建模与仿真技术的研究现状,就目前普遍采用的基于 Lagrange 方 程和角动量定理的多刚体模型法、仿真软件建模法、Hill 三元素法、黑箱训练等方法进行了详细的分析,并对研究趋 势进行了展望。 本文所综述的动力学建模与仿真验证方法对实现穿戴式外骨骼机器人和谐自然人机交互设计具有 重要的指导意义。 关键词:下肢生物力学建模;Lagrange 方程;角动量定理;Hill 模型;仿真软件建模;黑箱训练法 中图分类号: TP391 文献标志码:A 文章编号:1673⁃4785(2015)04⁃0518⁃10 中文引用格式:邵明旭,王斐,殷腾龙,等. 人体下肢生物力学建模研究进展[J]. 智能系统学报, 2015, 10(4): 518⁃527. 英文引用格式:SHAO Mingxu, WANG Fei, YIN Tenglong, et al. Progress on the research of human lower limb biomechanical modeling[J]. CAAI Transactions on Intelligent Systems, 2015, 10(4): 518⁃527. Research progress on the human lower limb biomechanical modeling SHAO Mingxu, WANG Fei, YIN Tenglong, LIU Jian (College of Information Science and Engineering, Northeastern University, Shenyang 110819, China) Abstract:The research on the biomechanical modeling and simulation of human lower limbs is an important content in the development of wearable exoskeleton robots. Theoretical and technical methods derived from this research can promote the process of biomechanics, rehabilitation medicine and prosthetic / orthotic devices. This work reviews the state⁃of⁃the⁃art techniques for modeling and simulating biomechanics of human lower limbs and makes analysis of popular methods, such as multi⁃body modeling , simulation software modeling, Hill three elements modeling and black box training modeling based on Lagrange equation and theorem of angular momentum. The future prospects in this research field are also provided in this paper. The biomechanical modeling and simulating methods discussed is of great significance to the design of naturally harmonious human⁃robot interaction of wearable exoskeleton robots. Keywords:biomechanical modeling of human lower limb; Lagrange equation; theorem of angular momentum; Hill model; simulation software modeling; black box training modeling 收稿日期:2015⁃03⁃24. 网络出版日期:2015⁃07⁃02. 基金项目:中央高校基础科研业务费资助项目( 120124002);辽宁省自 然科学基金资助项目(2013020040). 通信作者:王斐. E⁃mail: wangfei@ ise.neu.edu.cn. 随着 MEMS、材料、控制和计算机技术的飞速发 展,以及我国快速进入老龄化社会后对康复辅助设 备的旺盛需求,穿戴式外骨骼机器人技术在世界范 围内引起了越来越多学者的关注。 但目前的动力外 骨骼和假肢研究存在的一个共性问题是对人体感觉 运动控 制、生物力学等知识了解不够,这就导致了 虽然设计出了先进的机器人硬件和软件,但由于没 有考虑人如何作用,因此设备在与人交互和协同方 面效果欠佳。 由于人体结构和功能的特殊性和复杂 性,建立一个能完全反映人体状态的生物力学模型

第4期 邵明旭,等:人体下肢生物力学建模研究进展 ·519 非常困难。为此,根据研究的目的,对人体或人体的 医学伦理性问题,肌肉的生物动力学参数测量具有 一部分作适当的简化,在一些必要的假设条件下,从 一定困难,现有的大部分下肢建模方式均未考虑人 不同角度出发,建立人体下肢的生物动力学模型有 体下肢的生物模型,只考虑下肢的典型结构,或是建 着巨大的意义山。 立简化后的下肢多刚体模型9】,或是用3D建模技 本文旨在对国内外人体下肢建模和仿真的最新 术模拟简易的人体下肢[1013),或是采用黑箱训练等 研究状况进行综述,并对今后的研究趋势进行阐述 方法跨过人体结构[),进而通过动力学分析方法描 分析,为进一步深入研究下肢生物动力学建模提供 述模型,并对模型进行求解。下面分别介绍几种典 一定的参考依据。 型的下肢建模方法。 1人体下肢结构概述 3.1 Lagrange多刚体模型 国内外的许多学者针对人体不同的运动或动作 从解剖学的角度看,人的躯体是由骨、骨连接和 情形,考虑不同情况下模型的具体要求,建立出了相 骨骼肌组成,全身骨骨间借关节连成骨骼,构成主体 应的多刚体模型,其中最简单的方法是用单质点模 人体支架。在运动过程中,骨、骨连接主要起杠杆作 拟人体运动,不过模型过于简单,实际价值较低。 用,而具体的肢体关节是运动的枢纽,骨骼肌是运动 Hanavan于1964年提出一个由15个多刚体环节组 的动力来源和主要执行部件。 成的,通过球铰系统连接的人体力学模型,这种模型 在人体下肢运动中起主要参与的骨骼如下:髋 将人体主要的生物结构简化为几何形状的均质刚 骨、股骨、腓骨、胫骨等。骨与骨之间主要由结缔组织 体,建立并计算出基于人体惯性参数的回归方程,是 连接,共同形成人体骨架,骨头之间连接的地方称为 一套比较完整的具有个性化参数特征的多刚体人体 关节。而在人体下肢运动中起重要作用的关节主要 模型,这个模型也在一段时间内被连续引用)。波 有3个:髋关节、膝关节和踝关节。髋关节为多轴性 兰学者Blajera等为了研究杂技演员在蹦床上腾空 关节,可做屈、伸、内收、外展、内旋、外旋和旋转运动, 翻跟斗的动作过程,建立了一个自由度为10的多刚 由于髋关节起到连接上下肢和承重的作用,其骨密度 体人体模型io。Anderson等在研究人垂直起跳直 较大,故而稳固性较好。膝关节是人体负重比例最 到达到最大高度过程中肌肉运动协调模式时,把人 大、结构最复杂的关节,其主要负责大腿和小腿的屈、 体简化为10段、具有54块肌肉的模型,并在此模型 伸运动,和某些特定位置下的小幅度旋转运动。踝关 的基础上进一步建立人在行走过程中行走距离和步 节主要负责脚掌的背屈、伸、内收和外展运动。 态与能量消耗间的关系[)。Pejhan等在基于步态 与此同时,对人体下肢运动充当动力元件的肌 动力学仿真分析的人体下肢假肢优化系统的设计研 肉主要有股直肌、股外侧肌、股内侧肌、腓肠肌、胫骨 究中,将人体下肢简化为6刚体的二维力学模型, 前肌等。其中股直肌、股内侧肌、股外侧肌主要负责 大腿伸和屈、小腿伸和屈、膝关节的伸和髋关节的 并使用经典的Lagrange动力学方程对其建模[1)。 屈,并保持人体直立姿势:腓肠肌和胫骨前肌主要负 多刚体建模方法的核心是不考虑肌肉组成结 责小腿屈伸和人体的直立、行走[24]。 构,把大腿、小腿、上肢等结构视作一个个刚体,从系 统能量或动力学角度,对人体下肢进行建模,其中主 2人体下肢力学建模方法分类 要有Newton-Euler方法、Lagrange方法、角动量方 从关节和肌肉角度2个出发,可以得到不同的 法、Kane方法等[i9-2],其中Lagrange建模法应用最 下肢模型。从关节角度出发可以得到膝关节、髋关 为广泛,下面以这种方法为例介绍典型多刚体建模 节和踝关节力矩:从肌肉角度出发可以得到肌肉力, 方法[24」 而且肌肉力进一步可合成关节力矩。考虑到外骨骼 Lagrange建模法的核心是建立人体下肢多刚体 发展趋势,操作者的舒适性和安全性变得越来越重 模型的Lagrange动力学方程。其中,多轴加速度传 要。从个性差异化骨骼肌模型出发的肌肉力模型因 感器用来检测大腿和小腿的倾角并获取下肢运动过 与人体下肢结构更为相似,符合人体下肢建模的仿 程中的姿态以及膝关节角度和角速度;足底压力传 生设计的出发点,具有先天优势,已成为近几年外骨 感器被用来检测下肢的脚与地面之间接触状态和作 骼的发展热点[s6]」 用力等信息。结合人体结构和运动学的分析方法, 3基于关节力矩的下肢建模方法 建立人体下肢运动数学模型。从系统能量角度出发 构建动力学模型,并对得到的下肢模型进行动力学 由于人体下肢有着复杂的生物结构,并且限于 分析,进而得到关节力矩
非常困难。 为此,根据研究的目的,对人体或人体的 一部分作适当的简化,在一些必要的假设条件下,从 不同角度出发,建立人体下肢的生物动力学模型有 着巨大的意义[1] 。 本文旨在对国内外人体下肢建模和仿真的最新 研究状况进行综述,并对今后的研究趋势进行阐述 分析,为进一步深入研究下肢生物动力学建模提供 一定的参考依据。 1 人体下肢结构概述 从解剖学的角度看,人的躯体是由骨、骨连接和 骨骼肌组成,全身骨骨间借关节连成骨骼,构成主体 人体支架。 在运动过程中,骨、骨连接主要起杠杆作 用,而具体的肢体关节是运动的枢纽,骨骼肌是运动 的动力来源和主要执行部件。 在人体下肢运动中起主要参与的骨骼如下:髋 骨、股骨、腓骨、胫骨等。 骨与骨之间主要由结缔组织 连接,共同形成人体骨架,骨头之间连接的地方称为 关节。 而在人体下肢运动中起重要作用的关节主要 有 3 个:髋关节、膝关节和踝关节。 髋关节为多轴性 关节,可做屈、伸、内收、外展、内旋、外旋和旋转运动, 由于髋关节起到连接上下肢和承重的作用,其骨密度 较大,故而稳固性较好。 膝关节是人体负重比例最 大、结构最复杂的关节,其主要负责大腿和小腿的屈、 伸运动,和某些特定位置下的小幅度旋转运动。 踝关 节主要负责脚掌的背屈、伸、内收和外展运动。 与此同时,对人体下肢运动充当动力元件的肌 肉主要有股直肌、股外侧肌、股内侧肌、腓肠肌、胫骨 前肌等。 其中股直肌、股内侧肌、股外侧肌主要负责 大腿伸和屈、小腿伸和屈、膝关节的伸和髋关节的 屈,并保持人体直立姿势;腓肠肌和胫骨前肌主要负 责小腿屈伸和人体的直立、行走[2⁃4] 。 2 人体下肢力学建模方法分类 从关节和肌肉角度 2 个出发,可以得到不同的 下肢模型。 从关节角度出发可以得到膝关节、髋关 节和踝关节力矩;从肌肉角度出发可以得到肌肉力, 而且肌肉力进一步可合成关节力矩。 考虑到外骨骼 发展趋势,操作者的舒适性和安全性变得越来越重 要。 从个性差异化骨骼肌模型出发的肌肉力模型因 与人体下肢结构更为相似,符合人体下肢建模的仿 生设计的出发点,具有先天优势,已成为近几年外骨 骼的发展热点[5⁃6] 。 3 基于关节力矩的下肢建模方法 由于人体下肢有着复杂的生物结构,并且限于 医学伦理性问题,肌肉的生物动力学参数测量具有 一定困难,现有的大部分下肢建模方式均未考虑人 体下肢的生物模型,只考虑下肢的典型结构,或是建 立简化后的下肢多刚体模型[7⁃9] ,或是用 3D 建模技 术模拟简易的人体下肢[10⁃13] ,或是采用黑箱训练等 方法跨过人体结构[14] ,进而通过动力学分析方法描 述模型,并对模型进行求解。 下面分别介绍几种典 型的下肢建模方法。 3.1 Lagrange 多刚体模型 国内外的许多学者针对人体不同的运动或动作 情形,考虑不同情况下模型的具体要求,建立出了相 应的多刚体模型,其中最简单的方法是用单质点模 拟人体运动,不过模型过于简单,实际价值较低。 Hanavan 于 1964 年提出一个由 15 个多刚体环节组 成的,通过球铰系统连接的人体力学模型,这种模型 将人体主要的生物结构简化为几何形状的均质刚 体,建立并计算出基于人体惯性参数的回归方程,是 一套比较完整的具有个性化参数特征的多刚体人体 模型,这个模型也在一段时间内被连续引用[15] 。 波 兰学者 Blajera 等为了研究杂技演员在蹦床上腾空 翻跟斗的动作过程,建立了一个自由度为 10 的多刚 体人体模型[16] 。 Anderson 等在研究人垂直起跳直 到达到最大高度过程中肌肉运动协调模式时,把人 体简化为 10 段、具有 54 块肌肉的模型,并在此模型 的基础上进一步建立人在行走过程中行走距离和步 态与能量消耗间的关系[17] 。 Pejhan 等在基于步态 动力学仿真分析的人体下肢假肢优化系统的设计研 究中,将人体下肢简化为 6 刚体的二维力学模型, 并使用经典的 Lagrange 动力学方程对其建模[18] 。 多刚体建模方法的核心是不考虑肌肉组成结 构,把大腿、小腿、上肢等结构视作一个个刚体,从系 统能量或动力学角度,对人体下肢进行建模,其中主 要有 Newton⁃Euler 方法、 Lagrange 方法、角动量方 法、Kane 方法等[19⁃23] ,其中 Lagrange 建模法应用最 为广泛,下面以这种方法为例介绍典型多刚体建模 方法[24] 。 Lagrange 建模法的核心是建立人体下肢多刚体 模型的 Lagrange 动力学方程。 其中,多轴加速度传 感器用来检测大腿和小腿的倾角并获取下肢运动过 程中的姿态以及膝关节角度和角速度;足底压力传 感器被用来检测下肢的脚与地面之间接触状态和作 用力等信息。 结合人体结构和运动学的分析方法, 建立人体下肢运动数学模型。 从系统能量角度出发 构建动力学模型,并对得到的下肢模型进行动力学 分析,进而得到关节力矩。 第 4 期 邵明旭,等:人体下肢生物力学建模研究进展 ·519·

.520. 智能系统学报 第10卷 考虑到人体下肢在行走和跳跃等主要活动中踝 骤发展都较为成熟。在人体下肢生物动力学模型研 关节转动轻微,因此忽略踝关节的转动,将人体下肢 究的早期,研究者们多用此方法来描述人体的运动 结构简化为平面的二刚体模型如图1所示。其中, 规律。 H表示髋关节,K为膝关节,A为踝关节。T和S分 1)选取关节广义变量及广义力 别代表大腿和小腿的质心。 首先选取笛卡尔坐标系,将大腿和小腿的关节 变量分别定义为运动过程中大腿和小腿的转角 H 和02,M。和M4分别代表髋关节和膝关节的力矩。 m1和m2分别表示大腿和小腿的质量,大、小腿长分 别为l和L2,质心分别用T和S代替,与关节中心的 距离分别为P,和p2。如上所述,大腿质心T的位置 坐标可用一组坐标描述: mg X=pisin 0 Y1=-P1c0s6 (3) 小腿质心S的位置坐标描述如下: X2=l1sin01+P2sin(01+02) Y2=-l1cos01-p2cos(91+02) (4) 2)系统动能K Ek=Ek +Eg a=ni诚Ba= 1 1 2m,14e+2m(0+0,)2+ m2l2p2(0+0,02)cos02 (5) 图1下肢二刚体二自由度模型 3)系统势能P Fig.1 The two rigid body and two de- E。=Eni+Ep2 grees of freedom model of lower E=migp (1 cos 0)E2 limb m282[1-c0s(01+02)]+ 在分析力学中,拉格朗日方程是解决受约束的 m2gl (1 -cos 0,) 质点系动力学问题的一个有力工具。拉格朗日函数 4)拉格朗日函数定义为 L被定义为系统动能K和势能P之差,即 L=Ek-E。 L=K-P (1) 5)系统动力学方程 其中系统动能K和势能P可以用任何方便的坐标 根据拉格朗日方程定义式计算各关节上的力 系来表示。用拉格朗日方程表示系统动力学方程式 矩,得到系统动力学方程。髋关节H上的力矩M 如下: 计算如下: d aLaL F:= (2) dt aq:aqi =(m,p+m,l9,+m,lp,(28,+,)cos8,+ a0, 式中:9:为表示动能和位能的坐标,9:为相应质点 m2P22(01+02) 的速度,而F:为作用在第i个坐标上的力或力矩。T aL 是作用在第i个坐标上的力或力矩,具体计算公式 a01 =-(m1P1+m2l1)gsin81-m2g2sin(81+02) 由9:为直线坐标或角坐标决定。这些力、力矩和坐 (7) 标分别称为广义力、广义力矩和广义坐标,n为连杆 得到 总数目。 d aL aL M6 (8) 用Lagrange方程解决实际力学问题是经典力 d业a8,a9, 学分析中一种非常成功的方法,具体内容和解题步 进一步简化为
考虑到人体下肢在行走和跳跃等主要活动中踝 关节转动轻微,因此忽略踝关节的转动,将人体下肢 结构简化为平面的二刚体模型如图 1 所示。 其中, H 表示髋关节, K 为膝关节, A 为踝关节。 T 和 S 分 别代表大腿和小腿的质心。 图 1 下肢二刚体二自由度模型 Fig.1 The two rigid body and two de⁃ grees of freedom model of lower limb 在分析力学中,拉格朗日方程是解决受约束的 质点系动力学问题的一个有力工具。 拉格朗日函数 L 被定义为系统动能 K 和势能 P 之差,即 L = K - P (1) 其中系统动能 K 和势能 P 可以用任何方便的坐标 系来表示。 用拉格朗日方程表示系统动力学方程式 如下: Fi = d dt ∂L ∂q · i - ∂L ∂qi (2) 式中: qi 为表示动能和位能的坐标, qi ˙ 为相应质点 的速度,而 Fi 为作用在第 i 个坐标上的力或力矩。 Ti 是作用在第 i 个坐标上的力或力矩,具体计算公式 由 qi 为直线坐标或角坐标决定。 这些力、力矩和坐 标分别称为广义力、广义力矩和广义坐标, n 为连杆 总数目。 用 Lagrange 方程解决实际力学问题是经典力 学分析中一种非常成功的方法,具体内容和解题步 骤发展都较为成熟。 在人体下肢生物动力学模型研 究的早期,研究者们多用此方法来描述人体的运动 规律。 1)选取关节广义变量及广义力 首先选取笛卡尔坐标系,将大腿和小腿的关节 变量分别定义为运动过程中大腿和小腿的转角 θ1 和 θ2 , Mh 和 Mk 分别代表髋关节和膝关节的力矩。 m1 和 m2 分别表示大腿和小腿的质量,大、小腿长分 别为 l 1 和 l 2 ,质心分别用 T 和 S 代替,与关节中心的 距离分别为 p1 和 p2 。 如上所述,大腿质心 T 的位置 坐标可用一组坐标描述: X1 = p1 sin θ1 Y1 = - p1 cos θ1 (3) 小腿质心 S 的位置坐标描述如下: X2 = l 1 sin θ1 + p2 sin θ1 + θ2 ( ) Y2 = - l 1 cos θ1 - p2 cos θ1 + θ2 ( ) (4) 2)系统动能 K Ek = Ek1 + Ek2 Ek1 = 1 2 m1 p 2 1 θ ·2 1Ek2 = 1 2 m2 l 2 1 θ ·2 1 + 1 2 m2 p 2 2 θ · 1 + θ · 2 ( ) 2 + m2 l 2 p2 θ ·2 1 + θ · 1 θ · 2 ( ) cosθ2 (5) 3)系统势能 P Ep = Ep1 + Ep2 Ep1 = m1 gp1 1 - cos θ1 ( ) Ep2 = m2 gp2 1 - cos θ1 + θ2 [ ( ) ] + m2 gl 1 1 - cos θ1 ( ) (6) 4)拉格朗日函数定义为 L = Ek - Ep 5)系统动力学方程 根据拉格朗日方程定义式计算各关节上的力 矩,得到系统动力学方程。 髋关节 H 上的力矩 Mh 计算如下 : ∂L ∂θ · 1 = m1 p 2 1 + m2 l 2 1 ( ) θ · 1 + m2 l 1 p2 2θ · 1 + θ · 2 ( ) cos θ2 + m2 p2 2 θ · 1 + θ · 2 ( ) ∂L ∂θ1 = - m1 p1 + m2 l 1 ( ) gsinθ1 - m2 gp2 sin θ1 + θ2 ( ) (7) 得到 Mh = d dt ∂L ∂θ · 1 - ∂L ∂θ1 (8) 进一步简化为 ·520· 智 能 系 统 学 报 第 10 卷
第4期 邵明旭,等:人体下肢生物力学建模研究进展 ·521· Mg=Du01+D1202+D20102+D12+D1(9) 系,但定义中不涉及力偶或力矩,并且运动量也不涉 膝关节K上的力矩M计算如下: 及角速度和角加速度。而角动量定理则描述了质点 =m,p(0,+a,)+m4p:8,es8, 系或刚体的运动量和力矩之间的关系。结合这2个 a02 定理就可完整地描述外力系与受力体运动参数之间 的定量关系。 aL a02 =-m2lP2(0+0,02)sin02- m2g2sin(81+02) (10) 进而得到 d aL aL M=a0,a0: (11) 进一步简化为 M=D101+Dn02+D20,82+ 速度运量运量定量 D26,2+D2 (12) (a)质点运动 最终得到人体下肢模型如下,带入大腿小腿质 量、关节角度等参数即可求得所需要的关节力矩: +C F(++dr) (13) d ) 式中: 面积速度→角动量→角动量定理 A-2 D.=Ds D B= (b)旋转状态 矩阵中详细参数如下: 图2质点运动及旋转状态示意图 Du mipi map2 m2l+2mzl pzcos 0 Fig.2 Sketch of the motion and rotating state of the particle D12=m2P3+m2l1P2c0s02 如图2所示,质点的运动状态以矢量形式定义: D21=m2P2+m1l1P2c0s62 (r、),相对某参考点的位置矢量为r,速度为v。 D22=m2P2 则动量定理为 D11=0 d(2mv)F·d (14) D122 =-m2liP2sin 02 Dau malipasin 02 惯性系$中的一个质点在相对某参考点O的运 D22=0 动过程中,其相对参考点0的径矢会相应的旋转。 Du=-2m2l Pzsin 02 假设在dt时间质点位移为vdt,转过的角度为d9, D121=0 r便会扫过面积dS: D22 =-m2l pasin 02 m2l pzsin 02 dsrxl (15) D =(mip m)gsin 0 m2p2gsin(0 +02) 面积速度为 D2=m2gP2sin(81+02) 3.2角动量定理建模法 di=rxv (16) 经典动力学研究中的3个定理分别为动量定 质点在惯性系S中相对参考点O的角动量L: 理、角动量定理和动能定理。Lagrange方程从能量 L=rXmw=r×p (17) 角度出发,应用动能定理和能量守恒建立和求解下 肢动力方程,而从角动量定理和动量定理角度出发 角动量L随时间的变化如下: 也可以建立人体多质点模型和多刚体模型的动力学 dL_d(r×p)_dr (18) dt dt dt xp+rx史 dt 方程252,求出关节力矩。 式中: 动量定理描述了物体的运动状态和力之间的关
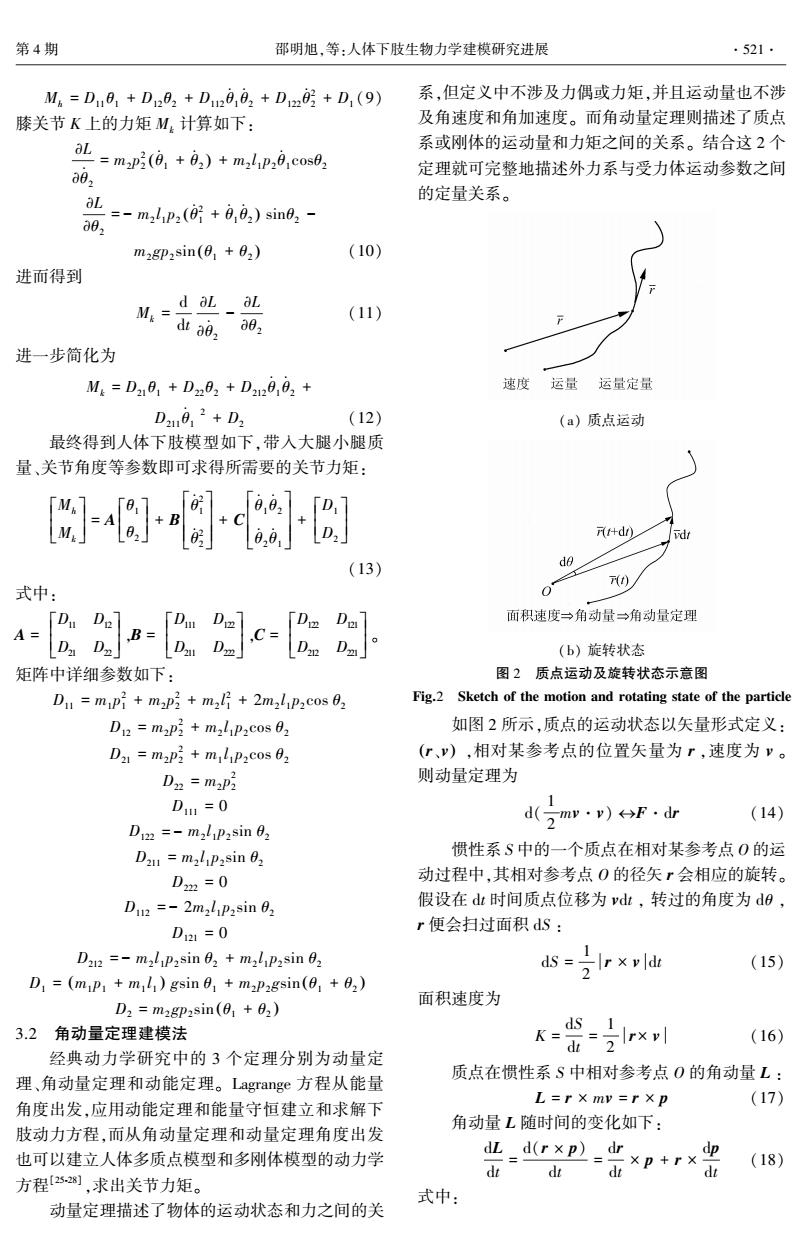
Mh = D11 θ ¨ 1 + D12 θ ¨ 2 + D112 θ · 1 θ · 2 + D122 θ ·2 2 + D1 (9) 膝关节 K 上的力矩 Mk 计算如下: ∂L ∂θ · 2 = m2 p 2 2 θ · 1 + θ · 2 ( ) + m2 l 1 p2 θ · 1 cosθ2 ∂L ∂θ2 = - m2 l 1 p2 θ ·2 1 + θ · 1 θ · 2 ( ) sinθ2 - m2 gp2 sin θ1 + θ2 ( ) (10) 进而得到 Mk = d dt ∂L ∂θ · 2 - ∂L ∂θ2 (11) 进一步简化为 Mk = D21 θ ¨ 1 + D22 θ ¨ 2 + D212 θ · 1 θ · 2 + D211 θ · 1 2 + D2 (12) 最终得到人体下肢模型如下,带入大腿小腿质 量、关节角度等参数即可求得所需要的关节力矩: Mh Mk é ë ê ê ù û ú ú = A θ ¨ 1 θ ¨ 2 é ë ê ê ù û ú ú + B θ ·2 1 θ ·2 2 é ë ê ê ê ù û ú ú ú + C θ · 1 θ · 2 θ · 2 θ · 1 é ë ê ê ê ù û ú ú ú + D1 D2 é ë ê ê ù û ú ú (13) 式中: A = D11 D12 D21 D22 é ë ê ê ù û ú ú ,B = D111 D122 D211 D222 é ë ê ê ù û ú ú ,C = D122 D121 D212 D221 é ë ê ê ù û ú ú 。 矩阵中详细参数如下: D11 = m1 p 2 1 + m2 p 2 2 + m2 l 2 1 + 2m2 l 1 p2 cos θ2 D12 = m2 p 2 2 + m2 l 1 p2 cos θ2 D21 = m2 p 2 2 + m1 l 1 p2 cos θ2 D22 = m2 p 2 2 D111 = 0 D122 = - m2 l 1 p2 sin θ2 D211 = m2 l 1 p2 sin θ2 D222 = 0 D112 = - 2m2 l 1 p2 sin θ2 D121 = 0 D212 = - m2 l 1 p2 sin θ2 + m2 l 1 p2 sin θ2 D1 = m1 p1 + m1 l 1 ( ) gsin θ1 + m2 p2 gsin θ1 + θ2 ( ) D2 = m2 gp2 sin θ1 + θ2 ( ) 3.2 角动量定理建模法 经典动力学研究中的 3 个定理分别为动量定 理、角动量定理和动能定理。 Lagrange 方程从能量 角度出发,应用动能定理和能量守恒建立和求解下 肢动力方程,而从角动量定理和动量定理角度出发 也可以建立人体多质点模型和多刚体模型的动力学 方程[25⁃28] ,求出关节力矩。 动量定理描述了物体的运动状态和力之间的关 系,但定义中不涉及力偶或力矩,并且运动量也不涉 及角速度和角加速度。 而角动量定理则描述了质点 系或刚体的运动量和力矩之间的关系。 结合这 2 个 定理就可完整地描述外力系与受力体运动参数之间 的定量关系。 (a) 质点运动 (b) 旋转状态 图 2 质点运动及旋转状态示意图 Fig.2 Sketch of the motion and rotating state of the particle 如图 2 所示,质点的运动状态以矢量形式定义: (r、v) ,相对某参考点的位置矢量为 r ,速度为 v 。 则动量定理为 d( 1 2 mv·v) «F·dr (14) 惯性系 S 中的一个质点在相对某参考点 O 的运 动过程中,其相对参考点 O 的径矢 r 会相应的旋转。 假设在 dt 时间质点位移为 vdt , 转过的角度为 dθ , r 便会扫过面积 dS : dS = 1 2 r × v dt (15) 面积速度为 K = dS dt = 1 2 r × v (16) 质点在惯性系 S 中相对参考点 O 的角动量 L : L = r × mv = r × p (17) 角动量 L 随时间的变化如下: dL dt = d(r × p) dt = dr dt × p + r × dp dt (18) 式中: 第 4 期 邵明旭,等:人体下肢生物力学建模研究进展 ·521·

·522. 智能系统学报 第10卷 dr 骨骼康复机器人的动力学模型,以角度、角速度和角 Xp=v×p=0 dt 加速度作为输入信号,输出信号为髋、膝关节力矩, 二F (19) 进行逆动力学仿真分析,获得了外骨骼逆动力学动 dt 态数学模型[35]。 于是 3.4SVR黑箱训练法 d业=rF (20) 下肢多刚体模型实质上采用传统的动力学方程 d 求解,具有模型精准度不高,计算关节力矩受参数影 质点所受到相对参考点O的力矩为 响大,不利于实时控制等缺点。针对这些缺点,Wi M= =rxF (21) Meng等提出了SVR黑箱训练法对下肢进行建模, dt 彻底放弃考虑人体下肢结构,并且证明该方法有利 根据下肢的平面二刚体模型,由角动量定理可 于实时控制。该方法从4个下肢肌肉提取的EMG 以得出: 信号均方根值(RMS)作为输入向量,以力传感器采 髋关节力矩为 集到的下肢关节力矩作为训练数据,将其输入支持 M=J 0 mip 01 migpisin 0 (22) 向量回归(SVR)模型来估算下肢关节力矩。使用自 膝关节力矩为 回归算法来构建EMG信号和下肢关节力矩之间的 Me=J202 m2p02 -m2gp2sin 62 (23) 关系8】。 式中:J和J2分别代表实验对象的大、小腿固有转 在本方法中,$VR算法被用来预测下肢力量与 动惯量。 肌电信号之间的关系。SVR黑箱算法的一个关键 3.3仿真软件建模法 问题是用函数来最大限度的接近模型,即找到一个 仿真软件建模属于多刚体建模法中的一种,将 确定性的函数g(x)代替模型本身非确定性函数 人体下肢主要结构在ADAMS或SimMechanics等仿 f(x),可用式(24)进行说明: 真分析或工业设计软件中用一些环节和约束函数代 替,再由视频采集软件或运动姿态采集设备提供肢 R(f.g)=L(f.g)dx (24) 体角度、大小腿长度等输入参数,通过软件强大的仿 其中,L(f,g)代表惩罚函数。函数f(x)表示样本 真功能,直接输出想要得到的关节力矩93。 序列,g(x)可以通过回归分析来获得。最后,SVR 在国内,朱昌义等在研究人体在做单杠摆运动 模型的求解可被转换为一组拉格朗日对偶问题,最 过程特点时,建立了一个5环节组成的多刚体力学 优化目标函数和约束条件如下: 模型,并且结合经典力学分析中的Kane方程,推导 min(O++03) 出人体行走步态规划过程中下肢摆动的动力学方 程)。刘明辉等在对外骨骼机器的研究中把人体 2a,-a)g-g)(x) Q1= 21 简化成一个九连杆的多刚体模型,并在机械系统动 力学自动分析软件(automatic dynamic analysis of Q2= ae-) i=1 mechanical system,ADAMS)中建立了简化后的人体 多刚体模型,对人体行走模型及步态分析进行了仿 0-Za(e+y (25) i=1 真分析,该研究为在虚拟环境中模拟现实情况下人 约束如下: 机外骨骼刚柔耦合系统提供了实验依据别。沈凌 等在对人体下肢外骨骼假肢的研究过程中,建立了 (a:-a)=0 i=1 (26) 基于四连杆系统的膝关节模型,并利用Lagrange方 a:,a∈[0,C] 法推导出下肢动力学方程,最后在Pro/E(Prol Engi- 然后,可以得到模型的回归方程: neer)软件中建立了下肢假肢结构的仿真模型,通过 系统集成的动力学仿真功能,得出的膝关节角度变 )=∑a-a)(0+b(27) 化和输出力矩之间的关系曲线,为下肢动力学建模 式中:SV代表支持向量空间,a:、a;是拉格朗日乘 提供了一定的参考数据。 子系数向量,b为偏移量。利用核函数来描述线性 洪晓明等人通过Solidworks软件建立精确的三 SVR向量到非线性SVR向量的映射。它们之间的 维实体模型,联合Matlab/SimMechanics建立下肢外 映射关系如下:
dr dt × p = v × p = 0 dp dt = F (19) 于是 dL dt = r × F (20) 质点所受到相对参考点 O 的力矩为 M = dL dt = r × F (21) 根据下肢的平面二刚体模型,由角动量定理可 以得出: 髋关节力矩为 Mh = Jx1 θ ¨ 1 + m 2 1 p1 θ ¨ 1 - m1 gp1 sin θ1 (22) 膝关节力矩为 Mk = Jx2 θ ¨ 2 + m2 p 2 2 θ ¨ 2 - m2 gp2 sin θ2 (23) 式中: Jx1 和 Jx2 分别代表实验对象的大、小腿固有转 动惯量。 3.3 仿真软件建模法 仿真软件建模属于多刚体建模法中的一种,将 人体下肢主要结构在 ADAMS 或 SimMechanics 等仿 真分析或工业设计软件中用一些环节和约束函数代 替,再由视频采集软件或运动姿态采集设备提供肢 体角度、大小腿长度等输入参数,通过软件强大的仿 真功能,直接输出想要得到的关节力矩[29⁃31] 。 在国内,朱昌义等在研究人体在做单杠摆运动 过程特点时,建立了一个 5 环节组成的多刚体力学 模型,并且结合经典力学分析中的 Kane 方程,推导 出人体行走步态规划过程中下肢摆动的动力学方 程[32] 。 刘明辉等在对外骨骼机器的研究中把人体 简化成一个九连杆的多刚体模型,并在机械系统动 力学自动分析软件 ( automatic dynamic analysis of mechanical system, ADAMS)中建立了简化后的人体 多刚体模型,对人体行走模型及步态分析进行了仿 真分析,该研究为在虚拟环境中模拟现实情况下人 机外骨骼刚柔耦合系统提供了实验依据[33] 。 沈凌 等在对人体下肢外骨骼假肢的研究过程中,建立了 基于四连杆系统的膝关节模型,并利用 Lagrange 方 法推导出下肢动力学方程,最后在 Pro / E(Prol Engi⁃ neer)软件中建立了下肢假肢结构的仿真模型,通过 系统集成的动力学仿真功能,得出的膝关节角度变 化和输出力矩之间的关系曲线,为下肢动力学建模 提供了一定的参考数据[34] 。 洪晓明等人通过 Solidworks 软件建立精确的三 维实体模型,联合 Matlab / SimMechanics 建立下肢外 骨骼康复机器人的动力学模型,以角度、角速度和角 加速度作为输入信号,输出信号为髋、膝关节力矩, 进行逆动力学仿真分析,获得了外骨骼逆动力学动 态数学模型[35⁃37] 。 3.4 SVR 黑箱训练法 下肢多刚体模型实质上采用传统的动力学方程 求解,具有模型精准度不高,计算关节力矩受参数影 响大,不利于实时控制等缺点。 针对这些缺点,Wei Meng 等提出了 SVR 黑箱训练法对下肢进行建模, 彻底放弃考虑人体下肢结构,并且证明该方法有利 于实时控制。 该方法从 4 个下肢肌肉提取的 EMG 信号均方根值(RMS)作为输入向量,以力传感器采 集到的下肢关节力矩作为训练数据,将其输入支持 向量回归(SVR)模型来估算下肢关节力矩。 使用自 回归算法来构建 EMG 信号和下肢关节力矩之间的 关系[38] 。 在本方法中,SVR 算法被用来预测下肢力量与 肌电信号之间的关系。 SVR 黑箱算法的一个关键 问题是用函数来最大限度的接近模型,即找到一个 确定性的函数 g(x) 代替模型本身非确定性函数 f(x) ,可用式(24)进行说明: R(f,g) = ∫L(f,g) dx (24) 其中, L(f,g) 代表惩罚函数。 函数 f(x) 表示样本 序列, g(x) 可以通过回归分析来获得。 最后,SVR 模型的求解可被转换为一组拉格朗日对偶问题,最 优化目标函数和约束条件如下: min Q1 + Q2 + Q3 { } Q1 = 1 2 ∑ m i = 1 ai - a ∗ i ( ) aj - a ∗ j ( ) 〈xi,xj〉 Q2 = ∑ m i = 1 ai ε - yi ( ) Q3 = ∑ m i = 1 a ∗ i ε + yi ( ) (25) 约束如下: ∑ m i = 1 ai - a ∗ i ( ) = 0 ai,a ∗ i ∈ [0,C] ì î í ï ï ïï (26) 然后,可以得到模型的回归方程: f(x) = ∑SV ai - a ∗ i ( ) 〈xi·x〉 + b (27) 式中:SV 代表支持向量空间, ai 、 a ∗ i 是拉格朗日乘 子系数向量, b 为偏移量。 利用核函数来描述线性 SVR 向量到非线性 SVR 向量的映射。 它们之间的 映射关系如下: ·522· 智 能 系 统 学 报 第 10 卷