
电子双缝实验结果: ●让大量电子通过狭缝,短时间内在感光板上就得到干涉图 样,这显示了电子的波动性。 ●降低电子流的强度,让电子一个一个地通过狭缝,随着时 10 间的推移(重复多次),也得到与短时间大量电子通过狭 a 缝时一样的干涉图样,显示电子的波动性不依赖大量电子 100 聚集在一起,单个电子也有波动性。 b ●干涉图样实际上是由一个一个局域性很小的感光点(这些 3000 感光点记录下一个个电子的痕迹)组成的,电子到达屏上 20000 时,只落在一点,不是弥散成线、带或片,表明电子是作 为一个整体被吸收在感光底片上的,显示了电子的粒子性 700000
电子双缝实验结果: ⚫ 让大量电子通过狭缝,短时间内在感光板上就得到干涉图 样,这显示了电子的波动性。 ⚫ 降低电子流的强度,让电子一个一个地通过狭缝,随着时 间的推移(重复多次),也得到与短时间大量电子通过狭 缝时一样的干涉图样,显示电子的波动性不依赖大量电子 聚集在一起,单个电子也有波动性。 ⚫ 干涉图样实际上是由一个一个局域性很小的感光点(这些 感光点记录下一个个电子的痕迹)组成的,电子到达屏上 时,只落在一点,不是弥散成线、带或片,表明电子是作 为一个整体被吸收在感光底片上的,显示了电子的粒子性 10 100 3000 20000 700000

干涉图样不是一个电子一次形成的,而是大量电子(同一次实验中聚集成束的电 子,或者相同条件下多次重复实验中的单个电子)在位置分布上的统计规律 >以单个电子多次重复实验为例,当时间比较短时,感光底片 上电子(10个、100个)的分布没有什么规律 10 >当时间足够长时,感光底片上电子越来越多(3000-70000), 100 就会出现有的地方电子很密(电子出现的几率大),有的地 方几乎没有电子(电子出现的几率小),电子在底片上位置 3000 分布或密度分布(电子在某个位置出现的几率)构成了一个 有规律的干涉图样 20000 >从波的角度,干涉条纹反映了波的强度,从粒子的角度,干 70000 涉条纹反映了电子出现的几率
⚫ 干涉图样不是一个电子一次形成的,而是大量电子(同一次实验中聚集成束的电 子,或者相同条件下多次重复实验中的单个电子)在位置分布上的统计规律 10 100 3000 20000 70000 ➢以单个电子多次重复实验为例,当时间比较短时,感光底片 上电子(10个、100个)的分布没有什么规律 ➢当时间足够长时,感光底片上电子越来越多(3000-70000), 就会出现有的地方电子很密(电子出现的几率大),有的地 方几乎没有电子(电子出现的几率小),电子在底片上位置 分布或密度分布(电子在某个位置出现的几率)构成了一个 有规律的干涉图样 ➢ 从波的角度,干涉条纹反映了波的强度,从粒子的角度,干 涉条纹反映了电子出现的几率
实物粒子和与之相联系德布罗意波妙的关系 从波和粒子的角度考虑 ●从波的角度 从粒子的角度 干涉图样中的明暗条纹代表到达那 干涉图样实际上是由一个一个局域性很小的感 里的德布罗意波的强度—2= 光点(电子)组成的,明暗条件反应了电子密 ψ*ψ 度分布,明条纹处电子密集(出现的几率大) 暗纹处电子很少或没有电子(出现的几率小) 电子到达屏幕上某处的几率与该处的德布罗意波的强度成比例
实物粒子和与之相联系德布罗意波𝜓的关系 ——从波和粒子的角度考虑 ⚫ 从波的角度 干涉图样中的明暗条纹代表到达那 里的德布罗意波的强度—— 𝝍 𝟐 = 𝝍∗𝝍 ⚫ 从粒子的角度 干涉图样实际上是由一个一个局域性很小的感 光点(电子)组成的,明暗条件反应了电子密 度分布,明条纹处电子密集(出现的几率大), 暗纹处电子很少或没有电子(出现的几率小) 电子到达屏幕上某处的几率与该处的德布罗意波的强度成比例

1926,波恩(Max.Born)的统计解释 FIGURE 40.5 The double-slit experiment with electrons. Double slit de Broglie 在电子与屏幕上某一局域点相互作用前,单个电子象波一样同 wavelength 时穿过双缝,自己与自己干涉,电子穿过缝后最终将落到屏幕 Detector 上的哪一点,在双缝实验中无法确切预言,但可以肯定的是, : 电子到达屏上某处的几率与该处的德布罗意波的强度成比例。 Electron arrival positions on detector 电子在某处出现的几率大(小) 该处的电子密度大(小) Interference fringes 该处成明条纹(暗条纹) 该处的德布罗意波的强度大(小) v P∝|2=ψ*ψ Electron wave function
1926,波恩(Max. Born)的统计解释 在电子与屏幕上某一局域点相互作用前,单个电子象波一样同 时穿过双缝,自己与自己干涉,电子穿过缝后最终将落到屏幕 上的哪一点,在双缝实验中无法确切预言,但可以肯定的是, 电子到达屏上某处的几率与该处的德布罗意波的强度成比例。 电子在某处出现的几率大(小) 该处的电子密度大(小) 该处成明条纹(暗条纹) 该处的德布罗意波的强度大(小) 𝑷 ∝ 𝝍 𝟐 = 𝝍∗𝝍
对比经典粒子(子弹)和经典波(水波)类似的双缝实验一费曼物理学讲义第3卷 ■一机枪,发射的子弹(无规则地)沿着相当大 25 的角度散开,子弹一颗一颗的发射 ■铁甲板墙(子弹无法穿透),板墙上开有2个孔, 孔的大小刚好能让一颗子弹通过 GUN ■木墙后障,可以吸收打上去的子弹 ■后障前面有一个可以沿x方向移动的装有沙子的 WALL BACKSTOP 箱子(探测器),进入探测器的子弹都会留在 箱子里,可以用来清点射到箱子里的子弹数 子弹通过墙上的小孔达到后障上距离中心距离为x处的几率P是多少? 一定时间内到达探测器的子弹数 P= 定时间内打到后障上的子弹数
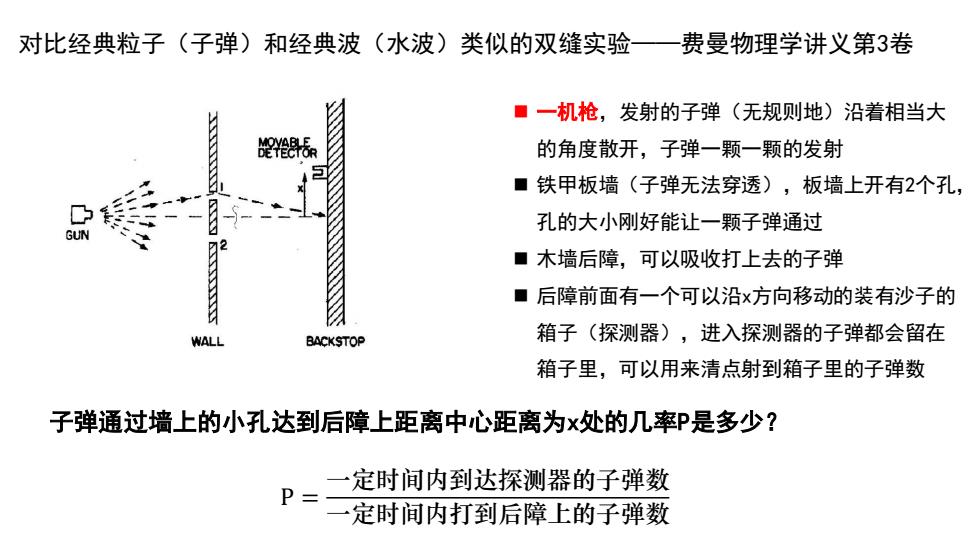
对比经典粒子(子弹)和经典波(水波)类似的双缝实验——费曼物理学讲义第3卷 ◼ 一机枪,发射的子弹(无规则地)沿着相当大 的角度散开,子弹一颗一颗的发射 ◼ 铁甲板墙(子弹无法穿透),板墙上开有2个孔, 孔的大小刚好能让一颗子弹通过 ◼ 木墙后障,可以吸收打上去的子弹 ◼ 后障前面有一个可以沿x方向移动的装有沙子的 箱子(探测器),进入探测器的子弹都会留在 箱子里,可以用来清点射到箱子里的子弹数 子弹通过墙上的小孔达到后障上距离中心距离为x处的几率P是多少? P = 一定时间内到达探测器的子弹数 一定时间内打到后障上的子弹数