
导期 动能定理(合力的功与动能变化的关系): mv2-mv 1 W合= ⑤ 功能关系 重力的功与重力势能变化的关系:Wc=⑤E1Ep2 机械能守恒定律 重力、弹力以外的其他力做的功与 机械能变化的关系:W其他=E2E1 条件:只有重力或弹力做功 机械能守恒定律〈 表达式:Ek1+Ep1=回 E2+Ep2或 Ep1-Ep2=⑧ Ek-Ek 实验:验证机械能守恒定律
导航 功能关系 动能定理(合力的功与动能变化的关系): 𝑾合 = ⑮ 重力的功与重力势能变化的关系:𝑾 𝐆 = ⑯ 重力、弹力以外的其他力做的功与 机械能变化的关系:𝑾其他 = 𝑬 𝟐-𝑬 𝟏 机械能守恒定律 条件:只有重力或弹力做功 表达式:𝑬 𝐤 𝟏 + 𝑬 𝐩 𝟏 = ⑰ 或 𝑬 𝐩 𝟏-𝑬 𝐩 𝟐 = ⑱ 实验:验证机械能守恒定律 机械能守恒定律 𝟏𝟐 𝒎 𝒗 𝟐 𝟐 − 𝟏𝟐 𝒎 𝒗 𝟏 𝟐 Ep1 -Ep2 Ek2+Ep2 Ek2 -Ek1

导航 专题归纳突破 专题一功和功率 1.恒力做功的求解。 恒力做功,根据定义式W=Flcos a求功,其中F、为力的大小 和位移的大小,为力F与位移方向之间的夹角,且 0≤a≤180°
导航 专题一 功和功率 1.恒力做功的求解。 恒力做功,根据定义式W=Flcos α求功,其中F、l为力的大小 和位移的大小,α为力F与位移l方向之间的夹角,且 0°≤α≤180° 。 专题归纳突破

导 2.合力做功的求解。 方法一:先求合力F合,再用W合=F合Icos a求功。 方法二:先求各个力做的功W1、W2、W3…,再利用W合 =W+W2+W3十…求合力做的功。 方法三:利用动能定理求合力做功,W合=△Ek 3.平均功率和瞬时功率。 求解功率问题时,要明确是求平均功率还是求瞬时功率,一 般情况下平均功率用P=W求解,瞬时功率用P=Fvcos求解
导航 2.合力做功的求解。 方法一:先求合力F合,再用W合=F合lcos α求功。 方法二:先求各个力做的功W1、W2、W3 …… ,再利用W合 =W1+W2+W3+……求合力做的功。 方法三:利用动能定理求合力做功,W合=ΔEk。 3.平均功率和瞬时功率。 求解功率问题时,要明确是求平均功率还是求瞬时功率,一 般情况下平均功率用P= 求解,瞬时功率用P=Fvcos α求解。 𝑾 𝒕
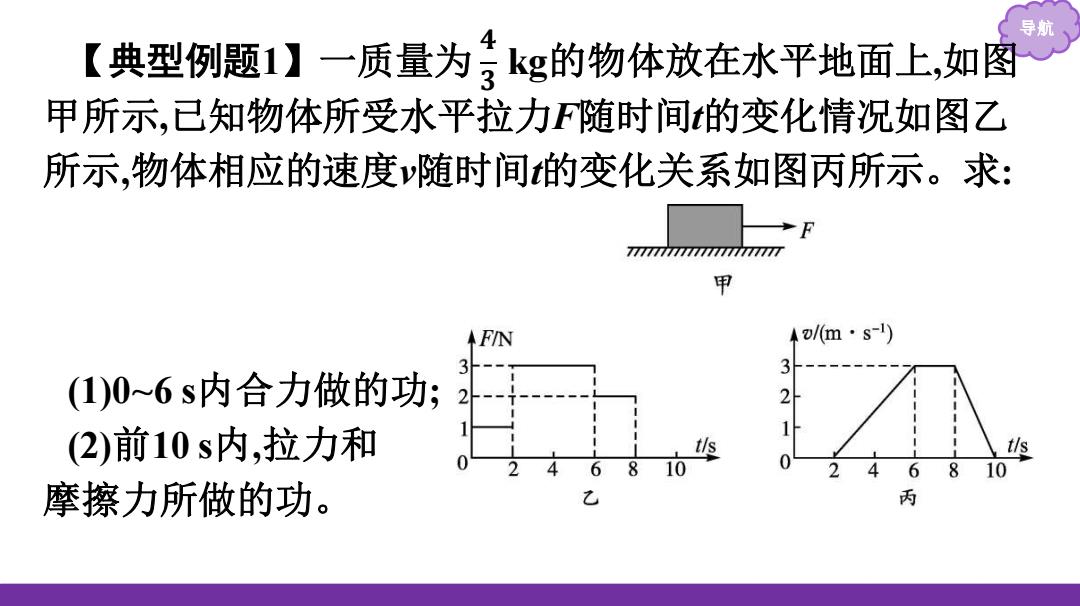
导 【典型例题1】一质量为kg的物体放在水平地面上,如图 甲所示,已知物体所受水平拉力F随时间t的变化情况如图乙 所示,物体相应的速度v随时间的变化关系如图丙所示。求: 甲 4/m·s-1) 3- (1)0~6s内合力做的功; 2 (2)前10s内,拉力和 t/s 2 6 10 摩擦力所做的功。 丙
导航 【典型例题1】一质量为 kg的物体放在水平地面上,如图 甲所示,已知物体所受水平拉力F随时间t的变化情况如图乙 所示,物体相应的速度v随时间t的变化关系如图丙所示。求: (1)0~6 s内合力做的功; (2)前10 s内,拉力和 摩擦力所做的功。 𝟒 𝟑

导航 答案:1)6 (2)30J-30J 解析:(1)由y-t图像可知物体初速度为零,6s末的速度为3m/s, 根据动能定理得W-之2-0,故合力做的功W子××32J=6J
导航 答案:(1)6 J (2)30 J -30 J 解析:(1)由v-t图像可知物体初速度为零,6 s末的速度为3 m/s, 根据动能定理得 W=𝟏 𝟐 mv2 -0,故合力做的功 W=𝟏 𝟐 × 𝟒 𝟑 ×3 2 J=6 J