
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
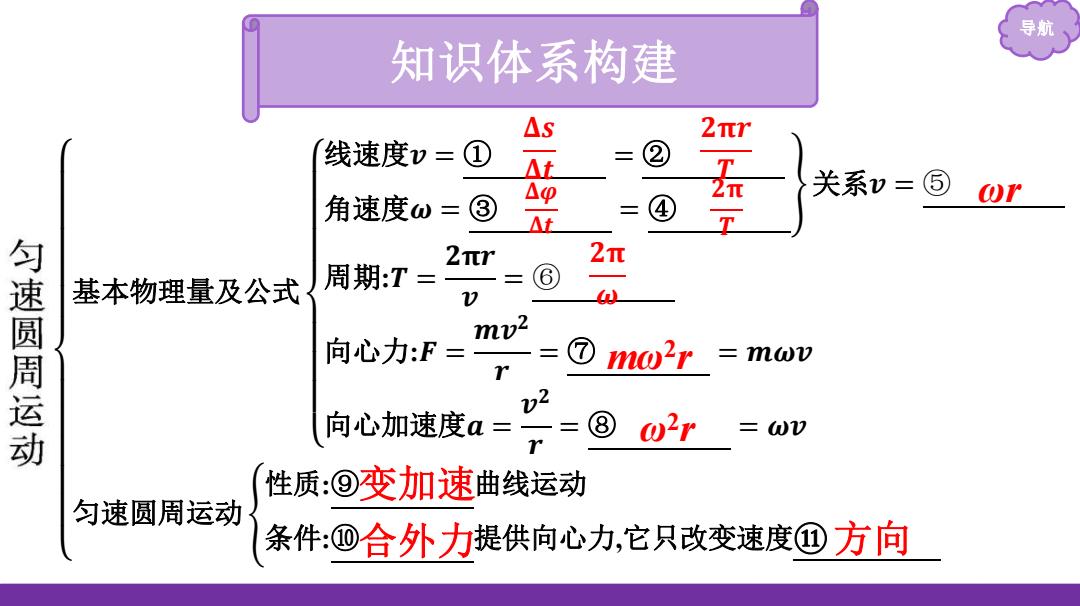
导航 知识体系构建 △S 2fr 线速度v = ① t △ 2π 关系v=⑤wr 角速度ω= ③ 三 △t 2πr 2π 匀速圆周运动 基本物理量及公式 周期:T= D mv2 向心力:F= ⑦ 三1 wv v2 向心加速度a= ⑧ 02r =ω) 性质:⑨变加速曲线运动 匀速圆周运动 条件:四合外力提供向心力,它只改变速度①方向
导航 基本物理量及公式 线速度𝒗 = ① = ② 角速度𝝎 = ③ = ④ 关系𝒗 = ⑤ 周期:𝑻 = 𝟐𝛑𝒓 𝒗 = ⑥ 向心力:𝑭 = 𝒎𝒗 𝟐 𝒓 = ⑦ = 𝒎𝝎𝒗 向心加速度𝒂 = 𝒗 𝟐 𝒓 = ⑧ = 𝝎𝒗 匀速圆周运动 性质:⑨ 曲线运动 条件:⑩ 提供向心力,它只改变速度⑪ 𝚫𝒔 𝚫𝒕 𝟐𝛑𝒓 𝑻 𝚫𝝋 𝚫𝒕 𝟐𝛑 𝑻 ωr 𝟐𝛑 𝝎 mω2 r ω2 r 变加速 合外力 方向 知识体系构建
导航 火车转弯的实例分析 匀速圆周运动 汽车过拱形桥:竖直平面内的圆周运动 圆周运动的实例分析 航天器中的失重现象 应用 离心运动 危害的防止
导航 圆周运动的实例分析 火车转弯的实例分析 汽车过拱形桥:竖直平面内的圆周运动 航天器中的失重现象 离心运动 应用 危害的防止

专题归纳突破 专题一圆周运动的动力学问题求解圆周运动的动力学问题 大致可以分为三步: 1.分析物体的运动情况,明确圆周运动的轨道平面,确定圆心 的位置和半径的大小,从而确定向心力的方向。 2.分析物体的受力情况,弄清向心力的来源。利用直接合成法 或正交分解法,求出沿半径方向的合力F,即为向心力。 3.由牛顿第二定律F=ma列方程求解相应问题,其中Fn是向心 力,是向心加速度,向心加速度往往用、or或把来表示
导航 专题一 圆周运动的动力学问题求解圆周运动的动力学问题 大致可以分为三步: 1.分析物体的运动情况,明确圆周运动的轨道平面,确定圆心 的位置和半径的大小,从而确定向心力的方向。 2.分析物体的受力情况,弄清向心力的来源。利用直接合成法 或正交分解法,求出沿半径方向的合力Fn ,即为向心力。 3.由牛顿第二定律Fn=ma列方程求解相应问题,其中Fn是向心 力,a是向心加速度,向心加速度a往往用 来表示。 𝒗 𝟐 𝒓 、ω2 r 或 r 𝟒𝛑 𝟐 𝑻𝟐 专题归纳突破