
第5卷第6期 智能系统学报 Vol.5 No.6 2010年12月 CAAI Transactions on Intelligent Systems Dec.2010 doi:10.3969/i.i8sn.1673-4785.2010.06.006 一 种新的混沌蚁群算法 及其在QS组播路由优化问题中的应用 孔笋,陈增强 (南开大学信息技术科学学院,天津300071) 摘要:基于QS的组播路由问题是通过发现具有某种相关性能约束的最佳组播树,来更好地利用网络资源以支持 应用的QS需求,作为以Q5为中心的网络体系结构中不可缺少的组成部分,目前已成为网络研究领域的重要内容 和热点问题.针对多约束条件下的QS组播路由问题,提出一种新的混沌蚁群算法.该算法基于传统的蚁群算法所 存在的不足,利用混沌优化算法对蚁群算法的运行参数进行动态地优化选择,自适应地改进了全局搜索能力和收敛 性.仿真实验结果表明,混沌蚁群算法比该文提到的遗传算法及蚁群算法在解决多约束组播路由问题上具有更好的 性能. 关键词:QS;组播路由;混沌算法;蚁群算法;参数优化 中图分类号:1P183;TN949.291文献标志码:4文章编号:16734785(2010)06049807 A new chaotic ant colony optimization algorithm and its application in a Qos multicast routing problem KONG Sun,CHEN Zeng-qiang (College of Information Technical Science,Nankai University,Tianjin 300071,China) Abstract:QoS-based multicast routing can take advantage of network resources to support an application with QoS requirements by searching for the optimal multicast tree with some performance constraints.This problem,which is an indispensable part of QoS-centered network architecture,has become an important issue in network domain re- search.A new chaotic ant colony optimization algorithm was proposed for a multi-constrained QoS multicast routing problem.To overcome the deficiencies of traditional ant colony algorithms,this algorithm uses a chaotic optimiza- tion algorithm to dynamically select parameters of the ant colony algorithm and improves global searching and con- vergence abilities.Simulation results show that this chaotic ant colony optimization algorithm performs better than the genetic algorithm and ant colony optimization mentioned here for solving a QoS multicast routing problem with multiple constraints. Keywords:QoS;multicast routing;chaos optimization algorithm;ant colony optimization algorithm;parameter opti- mization QoS组播路由的目的是在网络中寻找同时满足 化的组播路由算法受到了广泛研究,应用较成熟的 多用户对线路的带宽、延迟、延迟抖动、费用要求的 算法有遗传算法、神经网络算法、蚁群算法等26] 路由,即向多用户提供端到端的服务质量保证.Z. 其中,蚁群算法(ant colony algorithm,ACA)在 Wang等学者已经证明了包含2个及以上的约束条 深入研究中显示出了在求解复杂优化问题方面的优 件的QoS网络路由是一个NP完全问题,许多文 越性,被广泛用于解决各种具有NP难的问题.蚁群 献提出了解决该问题的有效算法.目前基于智能优 算法中的运行参数的选取对算法的收敛速度、全局、 局部搜索能力有着至关重要的影响,目前对于蚁群 收稿日期:2009-1124 算法运行参数的选取通常都是针对具体问题通过大 基金项目:国家“863”计划资助项目(2009AA04Z132):国家自然科学 基金资助项目(60774088). 量的数字仿真实验确定,缺乏理论的支持,因此传统 通信作者:孔笋.E-mai:ksuser(@mail.nankai..edu.cm. 的蚁群算法很难取得较好的寻优性能.在组播路由

第6期 孔笋,等:一种新的混沌蚁群算法及其在QS组播路由优化问题中的应用 ·499· 问题中,文献[7]提出一种用遗传蚁群算法来求解 3)bandwialth(P(s,t))=min bandwiath(e), QoS组播路由问题,采用遗传算法对蚁群算法的4 eEP(s,t); 个控制参数进行编码、优化操作,为参数的选择提供 4)delay_jitter(P(s))=delay_jitter(e) 了依据,更快地引导蚁群系统找到全局最优解;文献 delay_jitter(n); [8]基于蚁群算法的组播路由问题中,设计了一种 nepst) 自适应的挥发因子,用来控制算法的全局搜索能力; 5)packet_os(Pr(s,))=1-.及,(1-pack- 文献[9]提出一种改进的自适应蚁群算法,在信息 et_lass(n)). 素更新策略中引入全局最优系数,然后以全局最优 式中:Pr(s,t)为组播树T(s,M)上源点s到终点t 系数为条件来自适应调整挥发因子和信息素强度常 的路由路径.以下给出QoS组播路由问题中约束条 数 件的定义:进行QoS路由的目的寻找一棵组播树 考虑到混沌优化算法具有随机性、遍历性、规律 T(s),满足: 性的搜索特点,一些研究者将混沌优化算法与蚁群 1)延迟约束:delay(P,(s,t))≤D; 算法相结合来提高蚁群算法性能0),主要有以下 2)带宽约束:bandwidth(Pr(s,t))≥B; 几种结合形式:1)采用混沌初始化进行改善个体质 3)延迟抖动约束:delay_jitter(Pr(s,t))≤DJ; 量;2)在调整信息量中,加入混沌扰动,以使解跳出 4)包丢失率约束:packet_loss(Pr(s,t))≤PL,; 局部极值区间;3)使用混沌搜索算子在当前迭代的 5)费用约束:在满足上述4个约束条件下, 全局最优解附近搜索更好的解 cost(T(s,M))最小 与前面的混沌蚁群算法不同,文中结合蚁群算 其中:B、D、DJ、PL分别代表业务对网络带宽、延迟 法的参数特性,提出了一种新的混沌蚁群优化算法, 延迟抖动、包丢失率的约束限制.在本模型中假设所 其基本思想是采用混沌搜索对蚁群算法中的控制参 有的组播终点的带宽约束、延迟、延迟抖动和包丢失 数进行优化,从而得到更好的参数组合使蚁群系统 率约束均相同。 能更好、更快地找到全局最优解.文中将其应用于求 2蚁群算法及参数分析 解QoS组播路由问题,仿真结果显示混沌蚁群算法 的求解性能要优于遗传算法及蚁群算法, 本文将Dorigo等人提出的ACS算法「2-l3]中的 选路方式引入到基本的蚂蚁算法中,下面针对n个 1QoS组播路由问题描述 城市的旅行商问题(traveling salesman problem, 网络模型表示为赋权图G=(V,E)3,式中V TSP)给出相应的算法模型, 是图中所有网络节点组成的集合,E是网络双向链 1)路径选取原则. 路的集合,每一条边表示2个节点间的通信路径,假 蚁群算法是一种基于模型的搜索算法,它的搜 设网络是对称的.s∈V为源点,M∈{V-{s}}为终 索过程也是解的构造过程.对于求解TSP问题,当 点 蚂蚁在当前城市i选择下一个将要移动的城市⑧ 对于任一网络节点n∈V,定义4种属性,分别 时,依据式(1)、(2)给出的伪随机比例规则进行. 为:延迟函数delay(n)、延迟抖动函数 [arg,ma,r(·(t)i,i道q≤go; delay_.jitter(n)、包丢失率函数packet_.loss(n)、费用 else. 函数cost(n). (1) 对于任意链路e∈E,定义4种属性:延迟函数 P= delay(e),延迟抖动函数deday._jter(e),带宽函数 bandwidth(e)和费用函数cost(e). 「r(t)·t)/∑r()·()allowed; 0 else. 对于给定的源点s∈V,终点集合M,节点t∈M, (2) s和M组成的组播树T(s,M)存在下列关系: 式中:allowed={0,1,…,n-1}表示蚂蚁k下一步 1)delay(P,(s,))=eA.delay(e)+.eAn 允许选择的城市集合;r:为边(i,)上的信息素强 delay(n); 度;ng为边(i,)的能见度;a为信息启发式因子,表 2)cost(T(s,M))=.e8 ost(e)+An 示信息素对路径选择的重要性;B为期望启发式因 cost(n); 子,表示启发信息对路径选择的重要性;9是在[0

·500· 智能系统学报 第5卷 1]间均匀分布的随机数;90是一个可调参数(0≤ 索能力及其收敛速度,当ρ较大时,由于信息正反馈 9o≤1);S为根据是式(2)给出的概率分布所选出的 的作用占主导地位,以前搜索过的路径被再次选择 一个随机变量, 的可能性过大,搜索的随机性减弱;反之,当ρ很小 2)局部信息素更新规则. 时,信息正反馈的作用相对较弱,搜索的随机性增 当所有蚂蚁完成一次循环后,各路径上的信息 强,因此蚁群算法收敛速度很慢, 量要根据式(3)进行调整. 3 T(t+n)=(1-p1oeal)r(t)+p1oea△Ti, 基于混沌算法的蚁群算法参数优化 Ped∈(0,1). (3) 设计 式中:△rg=∑△r,PIeu表示路径上信息的蒸发系 3.1 k1 混沌优化 数;1-pu表示信息的保留系数;△rg表示本次循环 混沌优化是一种较新的优化算法,它利用混 路径可上信息的增量;△r表示第k只蚂蚁在本次循 沌序列的随机性、遍历性和初值敏感性来提高随机 环中留在路径可上的信息量,表示为 优化算法的效率.Logistic序列是这类算法中常用的 △r=QL,若第飞只蚂蚁在本次循环中经过护 混沌序列.它可以用式(5)来描述 0 其他, k+1=u·(1.0-x). (5) 式中:Q为常数,L:表示第k只蚂蚁在本次循环中所 式中:为常数,取值在[3.56,4.00]之间. 走过的路径的长度 不失一般性地,假设待优化问题为如下维函 3)全局信息素更新规则. 数的最小值问题: 所有蚂蚁走完全程,按式(4)进行信息素更新 Min f(x1,2,…,xn) T=(1 -Peobnl)T+peldATy, 式中:x:e[a,b:],i=1,2,…,n. Pgobe∈(0,1). (4) 其基本思想是首先产生一组与优化变量相同数 式中:Peba表示全局信息素的挥发系数;△rg表示 目的混沌变量,用类似载波的方式将混沌引入优化 为: △T前 变量使其呈现混沌状态,同时把混沌运动的遍历范 r1/Lm,若可为全局最优路径所经过的边; 围放大到优化变量的取值范围,然后直接利用混沌 10 其他 变量搜索。由于混沌运动具有随机性、遍历性、对初 式中:Lht为全局最佳路径长度. 始条件敏感性等特点,基于混沌的搜索技术无疑会 蚁群算法中的5个控制参数qa、a、B、Pieob 比其他随机搜索更具优越性, 的选取「1461对算法的性能有较大的影响.式中可调 3.2参数优化算法设计 参数取值较大,则多数蚂蚁易选择信息量最大的 本文提出的参数优化算法的思想是将蚁群算法 边,在搜索过程中可能容易出现多数蚂蚁搜索到相 的运行参数作为混沌算法的优化对象,在每一次迭 同的路径,使得搜索到的解空间较小,不利于发现全 代过程中,使用混沌搜索的当前值来运行蚁群算法 局最优解,算法容易收敛到局部最优解;若9取值 求解一标准优化问题,并使用适应值评价函数对求 较小,则信息量最大的边被选择的概率小,其他边被 解性能做出评价, 选择的概率大,能扩大搜索到的解空间,但搜索呈现 对于任一目的节点∈M(i=1,2,…,P),蚁群 一定的盲目性,不容易收敛信息启发式因子α的 以节点为单位进行寻径,并通过精简处理除去不满 大小反映了信息素因素作用的强度,其值越大,蚂蚁 足带宽约束的路径,构造混沌蚁群算法,求解满足所 选择以前走过路径的可能性越大,搜索的随机性减 有约束条件且总费用最小的组播路由, 弱,因此如果α值过大会使蚁群的搜索过早陷于局 基于上述规定和准则,构造的混沌蚁群算法具 部最优,而过小则会使算法收敛速度减慢.期望值启 体步骤如下: 发因子B的大小反映了先验性、确定性因素作用的 1)初始化参数.假定网络中有N个节点,给定 强度.其值越大,蚂蚁在某个局部点上选择局部最短 M只蚂蚁,循环次数为K,给定9o、aB、p1 enPlob初 路径的可能性越大,算法的随机性减弱,易于陷入局 始值及集合2中各备选路径的信息素初始值,给出 部最优;而B过小,将导致蚂蚁群体陷入纯粹的随机 各节点(d,DJ,PL,c)的值,以及每条存在边(d,DJ, 搜索,很难找到最优解.信息素挥发因子p1 Pgobel b,c)的值,并给出约束条件的D、DJ、PL、B的值. (这里统称ρ)的大小直接关系到蚁群算法的全局搜 2)蚂蚁从源节点开始按路径选择准则(1)随

第6期 孔笋,等:一种新的混沌蚁群算法及其在QS组播路由优化向题中的应用 ·501· 机选择下一个要行走的节点,启发函数?取 ③将混沌变量映射为优化变量,如式(8): 1/(cost(e:)+cost(n)),期望值启发因子B采用B/ y=a;+(b-a;). (8) :代替,使期望值在迭代的后期减少对路径选择的 ④利用适应值函数对当前所得到参数运行后 干扰,避免陷入局部最优,加快逼近最优解的速度. 的算法性能作出评价,适应值评价函数设计如下: 当每只蚂蚁对任一目的节点选择了一条路径,则对 Fit(s)=61L.(s)+82V(s)+63G(s), 该路径进行局部信息素更新;当M只蚂蚁对所有的 L(s)=Lave, 目的节点都选择了一条到达的路径后,根据目标函 Vi(s)=ewk 数[3]计算各蚂蚁的所对应的目标函数值,并进行比 G(s)=1/Gm 较,获得当前迭代最优组播树和全局最优组播树,若 式中:Fi(s)为第k次搜索所找到的算法参数所对 当前迭代最优组播树包含环路,则逆序查询,直到找 应的适应值;6、62、63为权系数,并满足61+62+ 到无环路组播树,将该树作为当前迭代最优组播树, 83=1;L,(s)表示蚁群算法搜索到的最优路径的能 最后对全局最优组播路径进行信息素的更新.对于 力;Lw。为M只蚂蚁寻找到的组播树的平均目标函 每项约束,本文假设各目的节点的约束限制相同,且 数值;V(s)表示蚁群算法的收敛速度:D是蚁群当 delay(Pr(s,t))delay_jitter(Pr(s,t))packet_ 前迭代次数;K为总迭代次数;G(s)表示蚁群算法 loss(P,(s,t))分别取组播树中源节点到达各目的 的全局搜索能力;G为蚁群5个参数变量的和. 节点的最大约束值,目标函数为式(6) ⑤经比较如果当前搜索到的参数使得适应度 1 =comt[), 函数偏大,则采用该参数进行下一轮寻径,若适应度 函数偏小,则继续混沌搜索,直到寻找到更优的参数 fa=Φ.(delay(Pr(s,t))-D), 或达到了最大步数 (中(z)= s0》 4)重复执行以上步骤,直到寻找到最优组播树. f=a(delay_jitter(Pr(s,t))-DJ), 4 仿真实验及比较 (Φg(z)= s0. 本文通过程序实现了混沌蚁群算法在解决QoS 组播路由优化的应用,仿真在Matlal7.0环境下实 fa=Φ,(packet_loss(Pr(s,t)-PL), 现.为了验证本文算法的有效性,本文采用了文献 (中(z)= 1,≤01 (6) [3]的网络结构模型进行实验仿真,并将混沌蚁群 ,2>0] 算法与应用于组播路由问题的遗传算法]、蚁群算 式中:Φ(z)是延时度量的惩罚函数,当满足延时约 法[8进行比较,网络拓扑图如图1所示: 束(delay(Pr(s,t)≤D)时,其值为l,否则等于ra (1,1,10,4)/ (0≤ra≤1);中(z)是延时抖动度量的惩罚函数,当 满足延时抖动约束(delay-jitter(P,(s,t)≤DJ)时, 9,0.80,2) (1.1.10,112 (183,100.9) 3,0,80,3) (5,1,10,1) 其值为1,否则等于T(0≤r≤1);中(z)是包丢失 5 3,1,1,10,2) (7,2.90.6) 率度量的惩罚函数,当满足包丢失率约束(packet_ 3,1,90,3) 3 loss(P(s,)≤PL))时,其值为1,否则等于tu(0≤ 6.1、30,8) 1 0,4) 3 (6.0 ra≤1);Ta Ta Tp三者的值的大小决定惩罚的程度. 9,1,120,1) 在本文试验仿真中,ra=T=Tu=0.5. 6 (11,1,10.5) 3)将9、a、B、p1lp4ba作为待优化的混沌变 9 (2.0.10,9) 40.7) 量,并给定各参数相应的取值范围,利用Logistic映 (4,1,130,10) 1 射进行混沌搜索。 (12,2,80,12) (7,31,10,3) (2,0,10°,7) ①首先将5个参数变量利用式(7)映射为混沌 变量,取值范围为[0,1], 图18节点网络模型] x=(y-a)/(b,-a). Fig.1 Eight-node network3] (7) 仿真实验以节点1为源节点,以节点2、节点4、 式中:y为优化变量,y:∈[a,b:],i=1,2,…,n,x 节点5、节点7为目的节点,寻找满足约束条件的最 为混沌变量。 优路径.参数go、aBp1 elobel为优化对象,初始值 ②用式(5)对混沌变量进行优化搜索
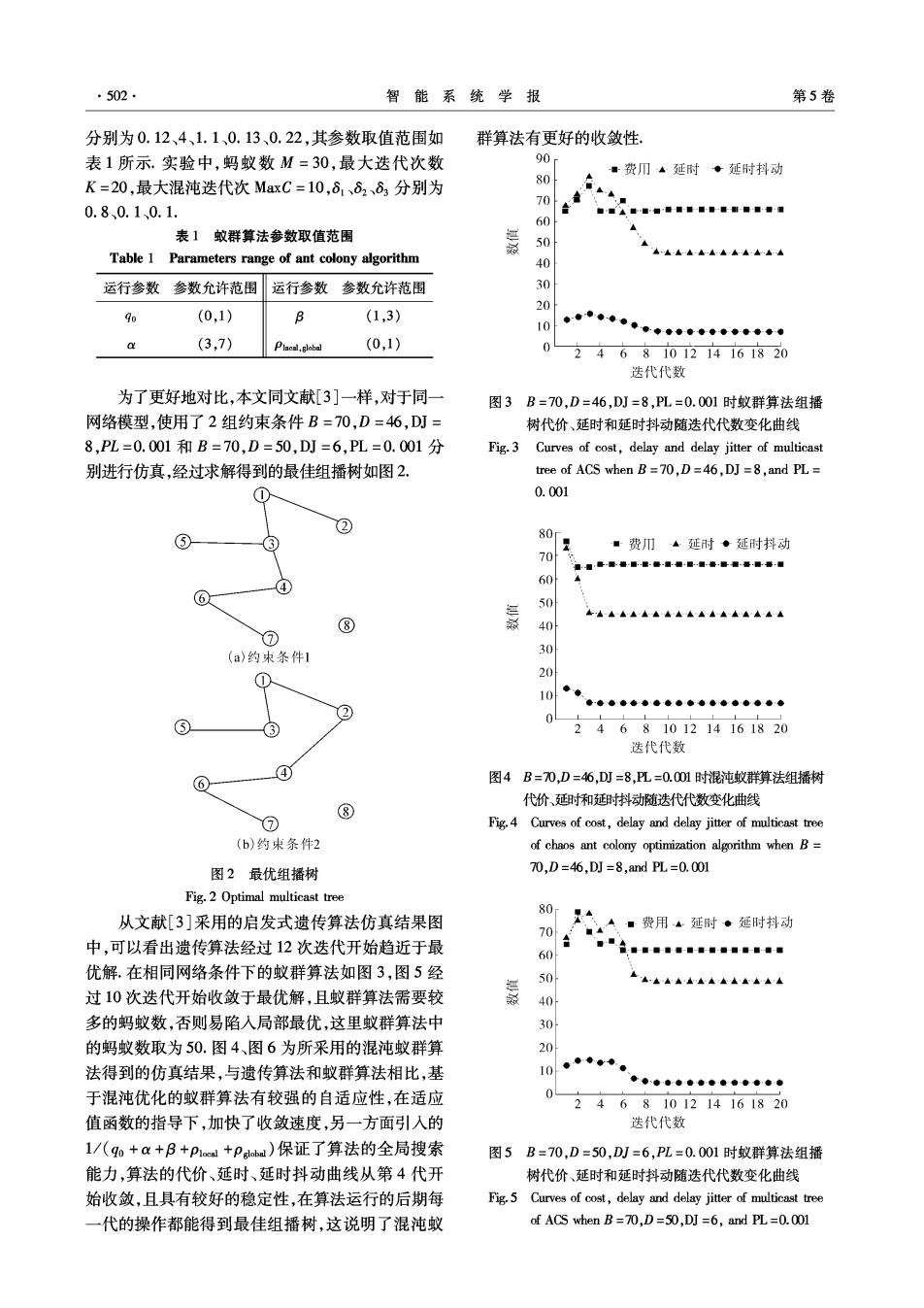
·502 智能系统学报 第5卷 分别为0.12、4、1.1、0.13、0.22,其参数取值范围如 群算法有更好的收敛性 表1所示.实验中,蚂蚁数M=30,最大迭代次数 90r ■费门▲延时◆延时抖动 K=20,最大混沌迭代次MaxC=10,81、82、83分别为 80 0.8、0.1、0.1. 70 6 表1蚊群算法参数取值范围 50 Table 1 Parameters range of ant colony algorithm 40 运行参数参数允许范围运行参数参数允许范围 30 20 分 (0,1) (1,3) 10 (3,7) Placal,global (0,1) 02468101214161820 迭代代数 为了更好地对比,本文同文献[3]一样,对于同一 图3B=70,D=46,DJ=8,PL=0.001时蚁群算法组播 网络模型,使用了2组约束条件B=70,D=46,DJ= 树代价、延时和延时抖动随迭代代数变化曲线 8,PL=0.001和B=70,D=50,DJ=6,PL=0.001分 Fig.3 Curves of cost,delay and delay jitter of multicast 别进行仿真,经过求解得到的最佳组播树如图2. tree of ACS when B=70.D=46.DJ =8,and PL= 0.001 ② ⑤ 0吖 ■费川▲延时·延时抖动 709 60 ⑥ 50 ⑧ 敏 40 ⑦ (a)约束条件1 30 ① io/ ●垂●●●海●●●●●●◆●●中◆◆ ② 0 ③ 2468101214161820 迭代代数 ⑥ ④ 图4B=70,D=46,DJ=8,PL=0.001时混沌蚁群算法组播树 代价、延时和延时抖动随迭代代数变化曲线 ① ⑧ Fig.4 Curves of cost,delay and delay jitter of multicast tree (b)约束条件2 of chaos ant colony optimization algorithm when B 图2最优组播树 70,D=46,DJ=8,and PL=0.001 Fig.2 Optimal multicast tree 从文献[3]采用的启发式遗传算法仿真结果图 80斯 ■费用▲延时·延时抖动 70 中,可以看出遗传算法经过12次迭代开始趋近于最 4 60 “台,g■ 优解.在相同网络条件下的蚁群算法如图3,图5经 50 L么么点AAA点4△人 过10次迭代开始收敛于最优解,且蚁群算法需要较 40 多的蚂蚁数,否则易陷入局部最优,这里蚁群算法中 30 的蚂蚁数取为50.图4、图6为所采用的混沌蚁群算 20A 法得到的仿真结果,与遗传算法和蚁群算法相比,基 10◆. 0 ●●◆●●◆◆●●●◆◆中 于混沌优化的蚁群算法有较强的自适应性,在适应 2468101214161820 值函数的指导下,加快了收敛速度,另一方面引入的 送代代数 1/(9o+&+B+p1oed+psbd)保证了算法的全局搜索 图5B=70,D=50,DJ=6,PL=0.001时蚁群算法组播 能力,算法的代价、延时、延时抖动曲线从第4代开 树代价、延时和延时抖动随迭代代数变化曲线 始收敛,且具有较好的稳定性,在算法运行的后期每 Fig.5 Curves of cost,delay and delay jitter of multicast tree 一代的操作都能得到最佳组播树,这说明了混沌蚁 of ACS when B=70,D=50,DJ=6,and PL=0.001