8-4理想气体的等温过程和绝热过程 物理学教程 (第二版) 等温过程 特征T=常量 1(p1,V,T) 过程方程pV 三常量 (P2,'2,T) dE =0 P2 热力学第一定律 dQ红=dW,=pdV Q,-W,-pdv RT 恒温热源 D=V 第八章热力学基础
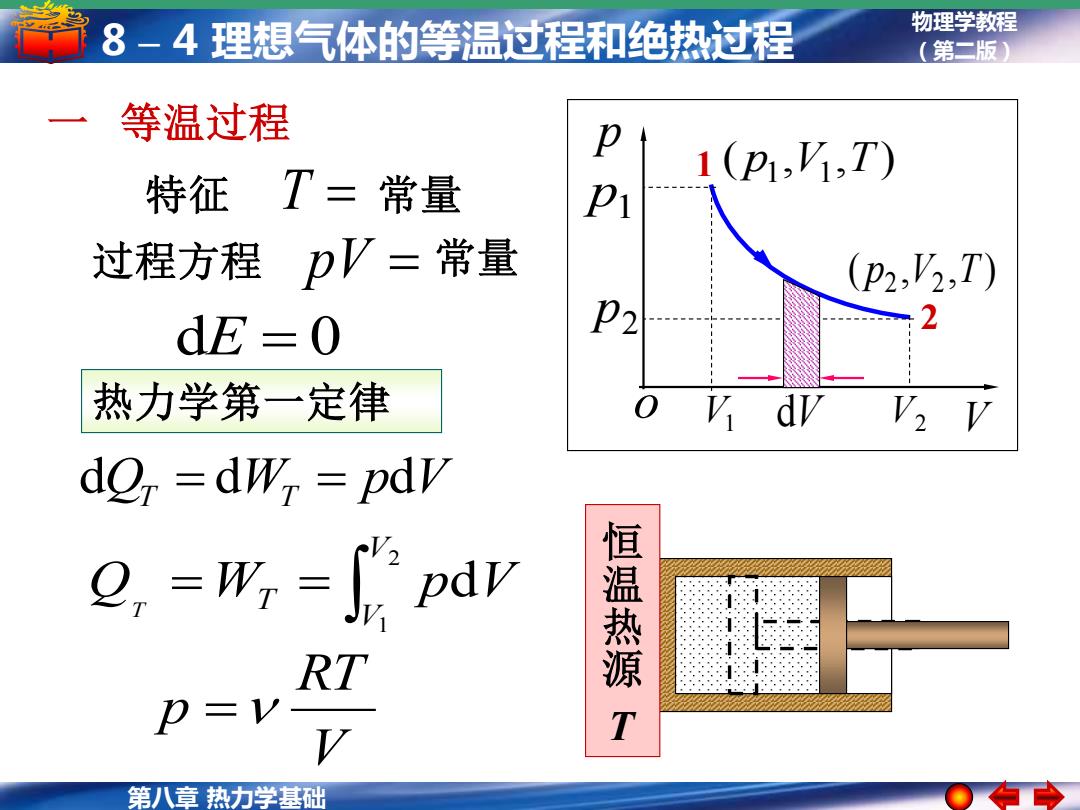
第八章 热力学基础 物理学教程 8 – 4 理想气体的等温过程和绝热过程 (第二版) 一 等温过程 热力学第一定律 dE = 0 恒 温 热 源 T V RT p = = = 2 1 d V V Q WT p V T dQT = dWT = pdV 1 2 ( , , ) p1 V1 T ( , , ) p2 V2 T p1 p2 V1 V2 p o dV V 特征 T = 常量 过程方程 pV = 常量
8-4理想气体的等温过程和绝热过程 物理学教程 (第二版) KL dy vRT I vRT In P2 等温膨胀 等温压缩 p 1(P1,V,T) p 1(p1,Vi,T) (p2,'2,T) (p2,'2,T) 2 P2 2 V2 V V2 V W 八音热学其出
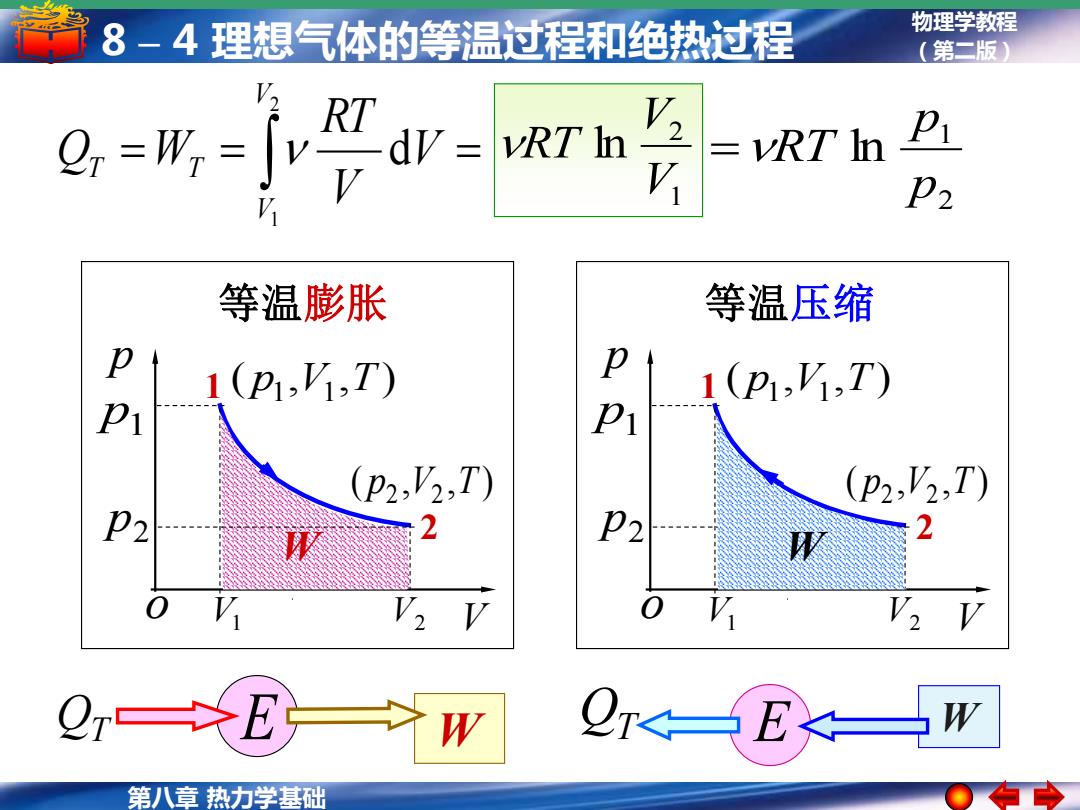
第八章 热力学基础 物理学教程 8 – 4 理想气体的等温过程和绝热过程 (第二版) E E = = = V V RT Q W V V T T d 2 1 1 2 ln V V RT 2 1 ln p p =RT 1 2 ( , , ) p1 V1 T ( , , ) p2 V2 T p1 p2 V1 V2 p o V 等温膨胀 W 1 2 ( , , ) p1 V1 T ( , , ) p2 V2 T p1 p2 V1 V2 p o V W 等温压缩 QT W QT W
8-4理想气体的等温过程和绝热过程 物理学教程 (第二版) 二 绝热过程 与外界无热量交换的过程 1(p1,V1,Ti) P 特征 do=0 热一律 dw.+dE =0 2,',T) P2 2 dW。=-dE dE =vCr.mdT V dv V,V 绝热的汽缸壁和活塞 形,=pd=-vc,d7 =-vCr.m(T2 -T) 第八章热力学基础
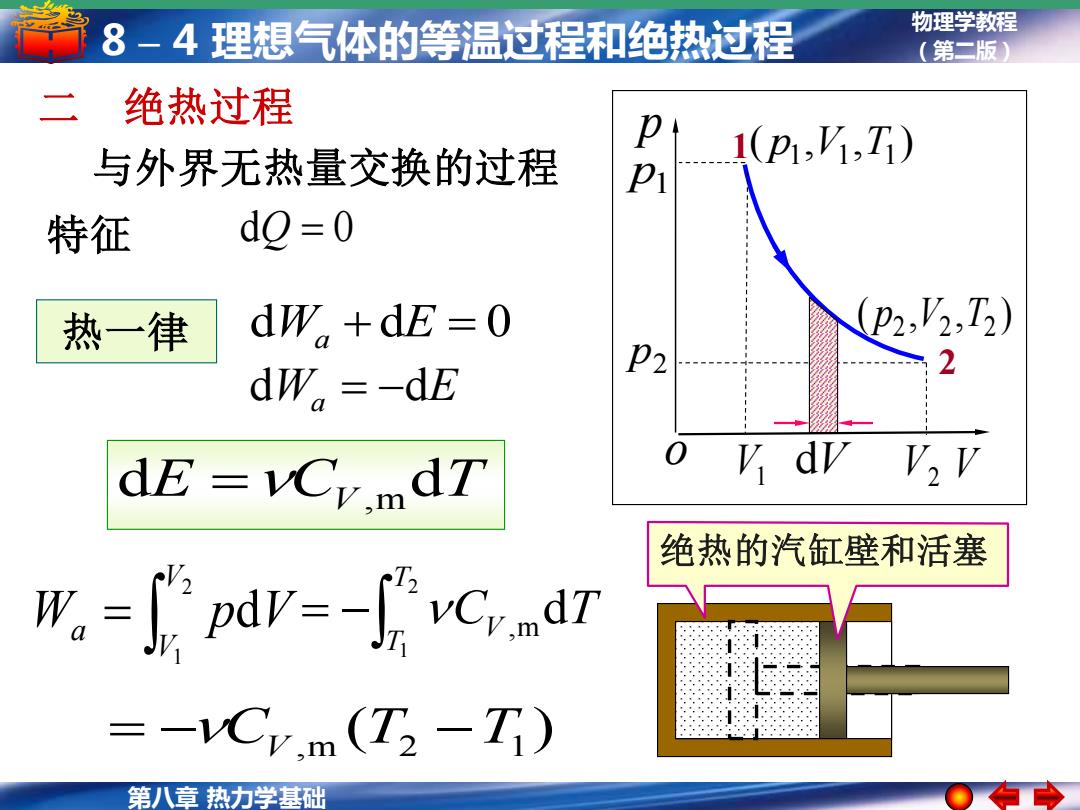
第八章 热力学基础 物理学教程 8 – 4 理想气体的等温过程和绝热过程 (第二版) ( , , ) p1 V1 T1 ( , , ) 2 V2 T2 p 1 2 p1 p2 V1 V2 p V o 二 绝热过程 与外界无热量交换的过程 ( ) = −CV ,m T2 −T1 特征 dQ = 0 CV T T T ,m d 2 1 = − dE =CV ,m dT = 2 1 d V V Wa p V dV 绝热的汽缸壁和活塞 dWa = −dE 热一律 dWa + dE = 0

8-4理想气体的等温过程和绝热过程 物理学教程 (第二版) 由热力学第一定律有 1(p1,V,Ti) W,=-△E Wa VCr.m (Ti-T2) (2,'2,T2) P2 她2 若已知p1,V1,p2,V2及Y V,V 从pP=7可格所C登-发) R Wa- (pW1-p22) C pm-Cvm w =pY-p2v y-1 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 4 理想气体的等温过程和绝热过程 (第二版) ( ) 1 1 2 2 ,m ,m ,m p V p V C C C W p V V a − − = 1 1 1 2 2 − − = p V p V Wa ( ) Wa =CV ,m T1 −T2 若已知 p1 ,V1 , p2 ,V2 及 ( , , ) p1 V1 T1 ( , , ) 2 V2 T2 p 1 2 p1 p2 V1 V2 p o V W Wa = −E pV =RT ( ) 1 1 2 2 ,m R p V R pV 从 可得 Wa = CV − 由热力学第一定律有

8-4理想气体的等温过程和绝热过程 物理学教程 (第二版) 绝热过程方程的推导 1(p1,V1,T1) .dQ=0,∴.dW=-dE 2=0 {ogwga7 (P2,'2,T2) P2 2 V RI dV=-WCnd7 V2 V 绝 V"-1T= 常量 分离变量得 .m dT R T pV”=常量 j d7 热方程 pTy=常量 第八章热力学基础
第八章 热力学基础 物理学教程 8 – 4 理想气体的等温过程和绝热过程 (第二版) 绝热过程方程的推导 dQ = 0, dW = −dE pdV = −CV ,m dT pV =RT V C T V RT d = − V ,m d T T V V d 1 d 1 − = − T T R C V dV V ,m d 分离变量得 = − ( , , ) p1 V1 T1 ( , , ) 2 V2 T2 p 1 2 p1 p2 V1 V2 p o V Q = 0 绝 热 方 程 = − V T 1 = pV = − − p T 1 常量 常量 常量