
*8-7熵熵增加原理 物理学教程 (第二版) 德国理论物理学家,他对 热力学理论有杰出贡献,曾提 出热力学第二定律的克劳修斯 表述为了说明不可逆过程,他 提出了熵的概念,并得出孤立 系统的熵增加原理。他还是气 体动理论的创始人之一. 克劳修斯 (1822-1888) 第八章热力学基础
第八章 热力学基础 物理学教程 *8 – 7 熵 熵增加原理 (第二版) 克劳修斯 (1822-1888) 德国理论物理学家,他对 热力学理论有杰出贡献,曾提 出热力学第二定律的克劳修斯 表述.为了说明不可逆过程, 他 提出了熵的概念,并得出孤立 系统的熵增加原理. 他还是气 体动理论的创始人之一

*8-7熵熵增加原理 物理学教程 (第二版) 熵 如何判断孤立系统中过程进行的方向? 可逆卡诺机 9-92_T7-T2 T 2 92 9 T T T 等温过程中吸收或放出的热量 热温比 T 与热源温度之比 结论:可逆卡诺循环中,热温比总和为零. 第八章热力学基础
第八章 热力学基础 物理学教程 *8 – 7 熵 熵增加原理 (第二版) 2 2 1 1 T Q T Q = 0 2 2 1 1 + = T Q T Q 结论 : 可逆卡诺循环中, 热温比总和为零 . T Q 热温比 等温过程中吸收或放出的热量 与热源温度之比 . 1 1 2 1 1 2 T T T Q Q Q − = − 可逆卡诺机 = 一 熵 如何判断孤立系统中过程进行的方向?
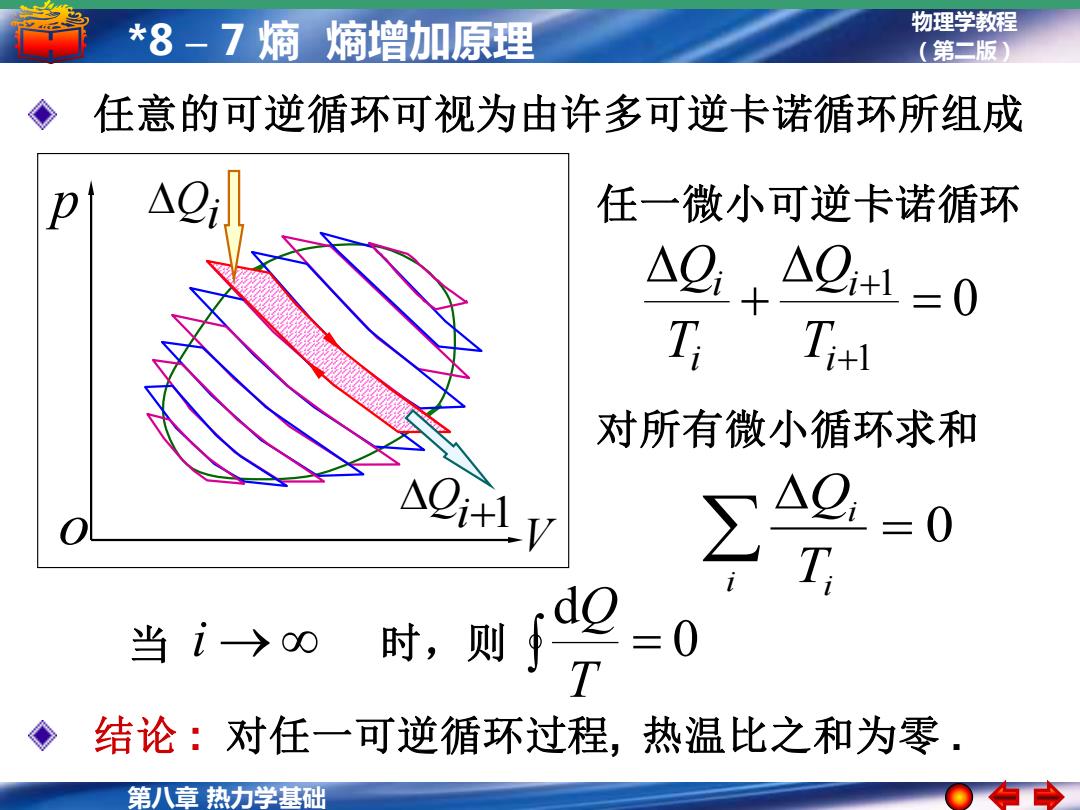
*8-7熵熵增加原理 物理学教程 (第二版) 任意的可逆循环可视为由许多可逆卡诺循环所组成 任一微小可逆卡诺循环 △Q △Q+1=0 T 对所有微小循环求和 1=0 当i>0时,则 2二0 结论:对任一可逆循环过程,热温比之和为零 第八章热力学基础
第八章 热力学基础 物理学教程 *8 – 7 熵 熵增加原理 (第二版) p o V 任一微小可逆卡诺循环 0 1 1 = + + + i i i i T Q T Q 对所有微小循环求和 = 0 i i i T Q 0 d → = T Q 当 i 时,则 任意的可逆循环可视为由许多可逆卡诺循环所组成 结论 : 对任一可逆循环过程, 热温比之和为零 . Qi +1 i Q

*8-7熵熵增加原理 物理学教程 (第二版) 9-ln 2+ja do ≥0 可逆过程 d№ =-SpR o T do T -J ao T 5。-S=d9 T 可逆过程 ◆ 在可逆过程中,系统从状态A改变到状态B,其热 温比的积分只决定于始末状态,而与过程无关.据此可 知热温比的积分是一态函数的增量,此态函数称熵. 第八章热力学基础
第八章 热力学基础 物理学教程 *8 – 7 熵 熵增加原理 (第二版) 0 d d d = + = ACB BDA T Q T Q T Q 在可逆过程中,系统从状态A改变到状态B , 其热 温比的积分只决定于始末状态,而与过程无关. 据此可 知热温比的积分是一态函数的增量,此态函数称熵. − = B B A A T Q S S d 可逆过程 p o V * * A C B D 可逆过程 BDA = −ADB T Q T dQ d ACB = ADB T Q T dQ d

*8-7熵熵增加原理 物理学教程 (第二版) 物理意义 热力学系统从初态A变化到末态B,系统熵 的增量等于初态A和末态B之间任意一可逆过程 热温比(dO/T)的积分. 可遮过程S。-S,-d9 dS do 无限小可逆过程 熵的单位 J/K 第八章热力学基础
第八章 热力学基础 物理学教程 *8 – 7 熵 熵增加原理 (第二版) 无限小可逆过程 T Q S d d = 热力学系统从初态 A 变化到末态 B ,系统熵 的增量等于初态 A 和末态 B 之间任意一可逆过程 热温比( dQ/T )的积分. 物理意义 熵的单位 J/K p o V * * A C B D E − = B B A A T Q S S d 可逆过程