
h,则v=[2]和h=[h,h2]就是该码字的度分布。 例如: 110100 H=111001 011010 该码字的度分布v1=1/2、v2=1/3、3=1/6,h3=2/3、h4=1/3 ②mΣ4 其码率可表示为: 1* +2*1 ∑w-2 +3*1 5 1 r=1- 3 6=1- ∑jh 2 3* 10 2 3 3 3 LDPC码的校验矩阵的行对应着校验方程(校验节点),列对应 着传输的比特(比特节点),它们之间的关系可以用Tanner图来表 示,图的左边有n个节点,每个节点表示码字的信息位,称为比特节 点,=1,2,,n,对应于校验矩阵的各列,比特节点也称为信息节 点或变量节点;右边有m个节点,每个节点表示码字的一个校验集, 称为校验节点{,=1,2,,m,代表校验方程,对应于校验节点的各 行;与校验矩阵中“1”元素相对应的左右两节点之间存在连接边。 我们将这条边两端的节点称为相邻节点,每个节点相连的边数成为该 节点的度(Degree),每个比特节点与j个校验节点相连,称为该比
hj,则 v=[v1, v2,..]和 h=[h1,h2,…]就是该码字的度分布。 例如: 110100 111001 011010 H = 该码字的度分布 v1=1/2、v2=1/3、v3=1/6,h3=2/3、h4=1/3 i j i j n iv m jh ⋅= ⋅ ∑ ∑ 其码率可表示为: 111 5 1* 2* 3* 236 3 1 11 1 2 1 10 2 3* 4* 33 3 i i j j i v r j h ⋅ + + =− =− =− = ⋅ + ∑ ∑ LDPC 码的校验矩阵的行对应着校验方程(校验节点),列对应 着传输的比特(比特节点),它们之间的关系可以用 Tanner 图来表 示,图的左边有 n 个节点,每个节点表示码字的信息位,称为比特节 点{xj, j=1, 2, …, n},对应于校验矩阵的各列,比特节点也称为信息节 点或变量节点;右边有 m 个节点,每个节点表示码字的一个校验集, 称为校验节点{ri, i=1, 2, …, m},代表校验方程,对应于校验节点的各 行;与校验矩阵中“1”元素相对应的左右两节点之间存在连接边。 我们将这条边两端的节点称为相邻节点,每个节点相连的边数成为该 节点的度(Degree),每个比特节点与 j 个校验节点相连,称为该比
特节点的度为;每个校验节点与k个信息节点相连,称为校验节点 的度为k。例如上面的H矩阵对应的Tanner图如下: 2 5=x1+x2+X4+x 3 5=x1+x3+x+X6 乃=X2+X3+X4+X6 X5 6 图1 Tanner图 LDPC码校验矩阵H中,一个很重要的概念:H矩阵的最小圈长, 即girth.。一个4循环(girth=4)在图1中表示为: 片=x1+X2+x4+x 3=X1+X3+X+x6 3=X3+X3+x4+X6 图2 Girth值为4的短循环
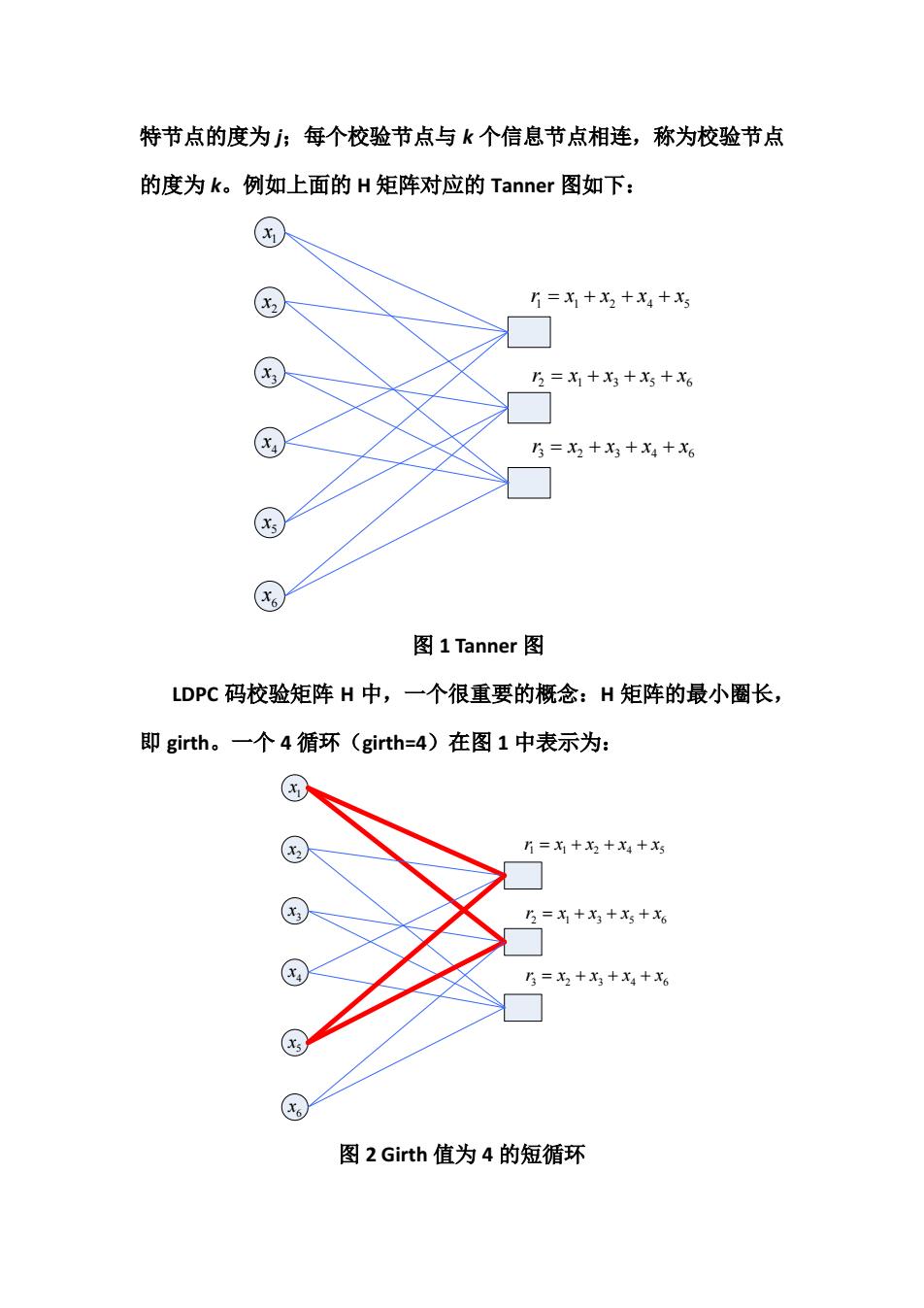
特节点的度为 j;每个校验节点与 k 个信息节点相连,称为校验节点 的度为 k。例如上面的 H 矩阵对应的 Tanner 图如下: 1 x 2 x 3 x 4 x 5 x 6 x 11245 rxxxx =+++ 2 1356 r xxxx =+++ 3 2346 rxxxx =+++ 图 1 Tanner 图 LDPC 码校验矩阵 H 中,一个很重要的概念:H 矩阵的最小圈长, 即 girth。一个 4 循环(girth=4)在图 1 中表示为: 1 x 2 x 3 x 4 x 5 x 6 x 11245 rxxxx =+++ 2 1356 r xxxx =+++ 3 2346 rxxxx =+++ 图 2 Girth 值为 4 的短循环

对应于H矩阵,此4循环可以表达为: 9 H=1 011101 同理,对于6循环我们有: 上式所示的矩阵H1表示校验矩阵H中的一个子矩阵。 短循环对于矩阵性能的影响:在LDPC码的译码算法中,我们都 假设传递的消息满足彼此独立的假设。当H矩阵中存在长度为2L的 环路时,则这些消息只在前L轮迭代过程中满足独立性假设(注意: 解码的迭代过程包括一次比特节点更新和一次校验节点更新)。因此 短循环的存在会影响LDPC码的解码性能。 另外简单的解释:例如在图2所示的H矩阵中,存在一个4循环 于是这个4循环对应的校验方程为: T=x1+X2+X4+X5 =X1+X3+X5+X6 由于4循环的存在,我们可以看到,上面两个校验方程含有共同 的比特节点x1与x5,直观地说,如果这两个校验方程均出错,则我
对应于 H 矩阵,此 4 循环可以表达为: 101 0 010 1 011101 = 1 1 H 1 1 同理,对于 6 循环我们有: 101 110 011 = H1 上式所示的矩阵 H1表示校验矩阵 H 中的一个子矩阵。 短循环对于矩阵性能的影响: 在 LDPC 码的译码算法中,我们都 假设传递的消息满足彼此独立的假设。当 H 矩阵中存在长度为 2L 的 环路时,则这些消息只在前 L 轮迭代过程中满足独立性假设(注意: 解码的迭代过程包括一次比特节点更新和一次校验节点更新)。因此 短循环的存在会影响 LDPC 码的解码性能。 另外简单的解释:例如在图 2 所示的 H 矩阵中,存在一个 4 循环 于是这个 4 循环对应的校验方程为: 11245 rxxxx =+++ 2 1356 r xxxx =+++ 由于 4 循环的存在,我们可以看到,上面两个校验方程含有共同 的比特节点 x1 与 x5,直观地说,如果这两个校验方程均出错,则我

们无法确定x1与x5中究竞哪个出错,所以从这个角度也可以说明短 循环对于性能带来的影响。 8.4LDPC码的编码方法 LDPC码属于线性分组码,利用其校验矩阵H可以生成编码矩阵G, 从而可以生成码字,其校验矩阵H可以体现LDPC码的特点与性能, 所以我们首先介绍H矩阵的构造方法。 8.4.1LDPC码校验矩阵H的构造 Gallager的H矩阵构造方法 ·每一行有j个1;一—满足行重要求 ·每一列有k个1;一一满足列重要求 ●任意两列具有共同1的个数不大于1;一满足gith值大于4 ●j和k分别与H矩阵中的列数和行数相比小得多;一一满足H 矩阵的稀疏性 设矩阵H为: Ho= 利用Ho,我们可以通过列交换的方法得到校验矩阵H: π(Ho) H= π2(H) .: π(H)】 例如下图就是由这种方法构造出的校验矩阵:
们无法确定 x1与 x5中究竟哪个出错,所以从这个角度也可以说明短 循环对于性能带来的影响。 8.4 LDPC 码的编码方法 LDPC 码属于线性分组码,利用其校验矩阵 H可以生成编码矩阵 G, 从而可以生成码字,其校验矩阵 H 可以体现 LDPC 码的特点与性能, 所以我们首先介绍 H 矩阵的构造方法。 8.4.1 LDPC 码校验矩阵 H 的构造 Gallager 的 H 矩阵构造方法 每一行有 j 个 1;——满足行重要求 每一列有 k 个 1;——满足列重要求 任意两列具有共同 1 的个数不大于 1;——满足 girth 值大于 4 j 和 k 分别与 H 矩阵中的列数和行数相比小得多;——满足 H 矩阵的稀疏性 设矩阵 H0为: 0 11...1 11...1 11...1 H = j { j { j { 利用 H0,我们可以通过列交换的方法得到校验矩阵 H: 1 0 2 0 0 ( ) ( ) ( ) k H H H π π π = H 例如下图就是由这种方法构造出的校验矩阵:

1111000000000000000 0000111100000000000 0000000011110000000 0 00000000000011110000 00000000000000001111 10001000100010000000 01000100010000001000 H=00100010000001000100 00010000001000100010 00000001000100010001 10000100000100000100 01000010001000010000 00100001000010000010 00010000100001001000 00001000010000100001 Mackay的构造方法 此方法中,校验矩阵的列重为,每行的平均重量为k(即此方法 所构造出的H矩阵),且任意两列具有共同1的个数不大于1(保证 不存在4循环)。 构造法1A 这是一种基本的构造方法,每一列具有固定的列重j。随机构造矩 阵,使其平均行重为k,且任意两列具有共同1的个数不大于1。构 造矩阵如图3所示: 3 3 图3(=3,k=6,R=1/2)
11110000000000000000 00001111 000000000000 000000001111 00000000 0000000000001111 0000 00000000000000001111 1 0001 0001 0001 0000000 01 0001 0001 0000001 000 001 0001 0000001 0001 00 0001 0000001 0001 0001 0 00000001 0001 0001 00 H = 0 1 1 00001 000001 000001 00 01 00001 0001 00001 0000 001 00001 00001 000001 0 0001 00001 00001 001 000 00001 00001 00001 00001 Mackay 的构造方法 此方法中,校验矩阵的列重为 j,每行的平均重量为 k(即此方法 所构造出的 H 矩阵),且任意两列具有共同 1 的个数不大于 1(保证 不存在 4 循环)。 构造法 1A 这是一种基本的构造方法,每一列具有固定的列重 j。随机构造矩 阵,使其平均行重为 k,且任意两列具有共同 1 的个数不大于 1。构 造矩阵如图 3 所示: 3 3 图 3(j=3,k=6,R=1/2)