
桥梁结构实验指导书 (土木水利学院土木工程专业桥梁方向本科生适用) 大连理工大学土木水利实验教学中心 桥梁工程实验室 2010年9月
1 桥梁结构实验指导书 (土木水利学院土木工程专业桥梁方向本科生适用) 大连理工大学土木水利实验教学中心 桥梁工程实验室 2010 年9 月

桥梁实验1一桥梁结构静态机械式仪表测试 (一)实验概况: 为了使桥梁设计更合理经济耐用在设计中进行模型实验是非常必要的。在桥 梁结构实验,需要测量的内容是多种多样的,如外力、变形、挠度、转角、曲率 几何变形等等。目前采用静力实验仪表也是比较多的。常用的机械仪表:有百分 表、千分表双杠引伸仪、手持应变仪、刚弦计、倾角仪等。 (二)实验目的: 1.使学生掌握机械仪表用途、使用方法和种类等。 2.使学生掌握各种仪表使用范围及精度等。 3.通过桥梁的模型实验加深理论与实践关系,加强桥梁实验重要性和必要 性。 4.增加学生理论与实践相结合的认识。 (三)实验内容 1.等强度梁的应变 等强度梁:为了使各个截面的弯曲应力相同,则应随着弯矩的大小相应 地改变截面尺寸,以保持相同强度的梁,这种梁称为等强度梁 R Rs 等强度梁如左图(等强度梁式力传感器)所示,梁厚为五,梁长为1,固定端 宽为6,自由端宽为b。梁的截面成等腰三角形,集中力F作用在三角形顶点。 梁内各横截面产生的应力是相等的,表面上任意位置的应变也相等,因此称为等 强度梁,其应变为
2 桥梁实验 1—桥梁结构静态机械式仪表测试 (一)实验概况: 为了使桥梁设计更合理经济耐用在设计中进行模型实验是非常必要的。在桥 梁结构实验,需要测量的内容是多种多样的,如外力、变形、挠度、转角、曲率、 几何变形等等。目前采用静力实验仪表也是比较多的。常用的机械仪表:有百分 表、千分表双杠引伸仪、手持应变仪、刚弦计、倾角仪等。 (二)实验目的: 1.使学生掌握机械仪表用途、使用方法和种类等。 2.使学生掌握各种仪表使用范围及精度等。 3.通过桥梁的模型实验加深理论与实践关系,加强桥梁实验重要性和必要 性。 4.增加学生理论与实践相结合的认识。 (三)实验内容: 1.等强度梁的应变 等强度梁:为了使各个截面的弯曲应力相同,则应随着弯矩的大小相应 地改变截面尺寸,以保持相同强度的梁,这种梁称为等强度梁 等强度梁如左图(等强度梁式力传感器)所示,梁厚为 h,梁长为 l,固定端 宽为 b0,自由端宽为 b。梁的截面成等腰三角形,集中力 F 作用在三角形顶点。 梁内各横截面产生的应力是相等的,表面上任意位置的应变也相等,因此称为等 强度梁,其应变为
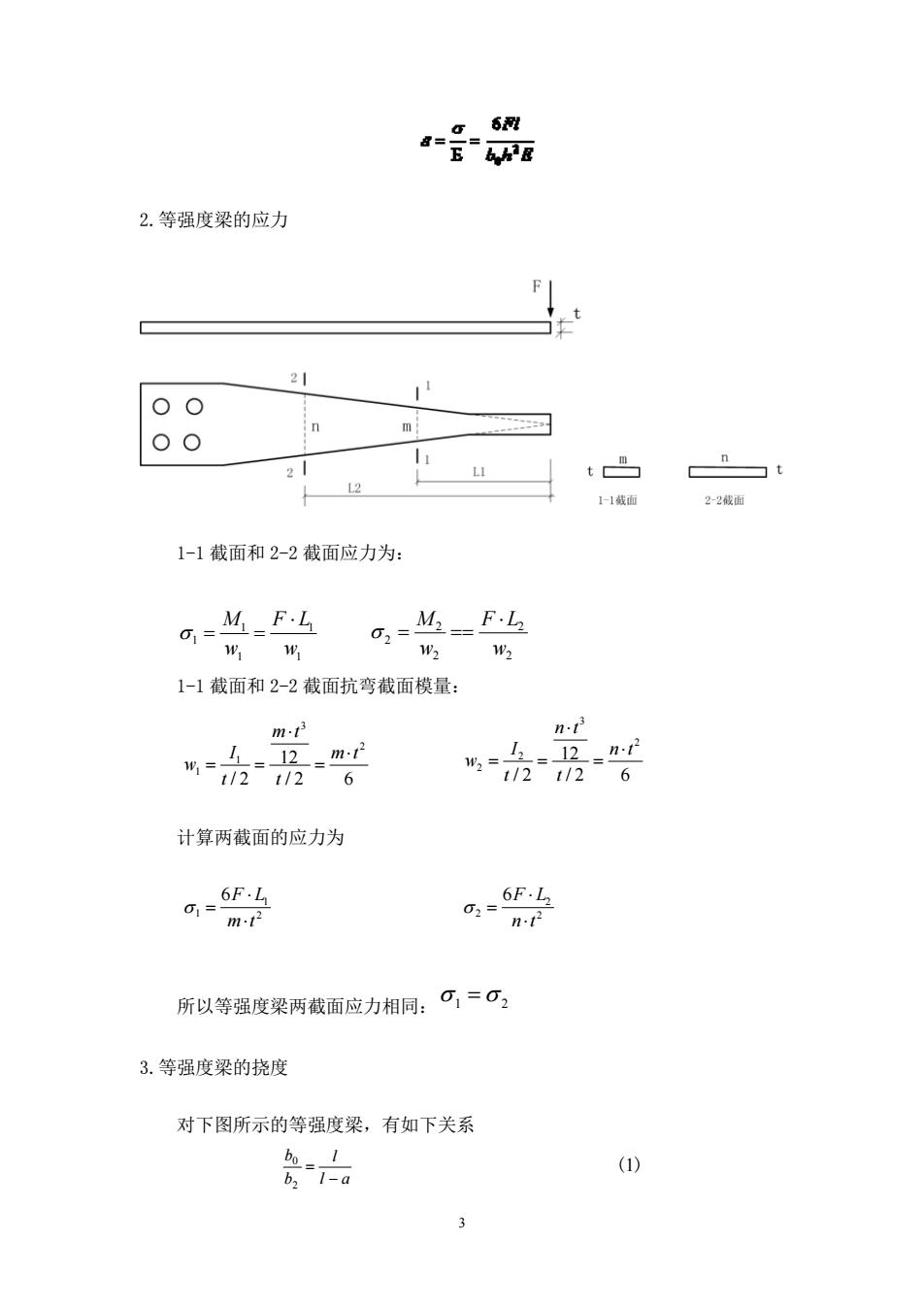
6别 4官 2.等强度梁的应力 21 00 00 t 11线 1-1截面和2-2截面应力为: a=M=F.L ,=4=F4 W2 1w2 1-1截面和2-2截面抗弯截面模量: mt 品房。 计算两截面的应力为 0=6F-5 m.t nt 所以等强度梁两截面应力相同:1=0 3.等强度梁的挠度 对下图所示的等强度梁,有如下关系 2-a )
3 2.等强度梁的应力 1-1 截面和 2-2 截面应力为: 1 1 1 1 1 M F L w w σ ⋅ = = 2 2 2 2 2 M F L w w σ ⋅ = == 1-1 截面和 2-2 截面抗弯截面模量: 计算两截面的应力为 所以等强度梁两截面应力相同:σ1 2 =σ 3.等强度梁的挠度 对下图所示的等强度梁,有如下关系 l a l b b − = 2 0 (1) 3 2 1 1 12 /2 /2 6 m t I m t w t t ⋅ ⋅ == = 3 2 2 2 12 /2 /2 6 n t I n t w t t ⋅ ⋅ == = 1 1 2 6F L m t σ ⋅ = ⋅ 2 2 2 6F L n t σ ⋅ = ⋅

b(1 X2 等强度梁的挠度计算 等强度梁段AB的横截面A对中性轴:的惯性矩1,和等截面梁段BC的横截 面对中性轴:的惯性矩,分别为 (2) 12 由(1)式和(2)式可得 会会2 (3) 对AB段(0≤x≤),梁在,截面处的宽度、对中性轴:的惯性矩和弯矩分 别为 44)40- 146)-4,=1,1-4 Mi()=-P(I-x) (4) 梁的挠曲线近似微分方程为 品 (5) 积分两次得到 =品+G 盘+G+0 (6) 利用边界条件O)=O)=0,可以得到C=D,=0,故梁在AB段的挠曲线 方程和转角方程分别为 4
4 a P l b2 b0 A B C h y x 2 x 1 z b (x ) 1 1 A B C x x 等强度梁的挠度计算 等强度梁段 AB 的横截面 A 对中性轴 z 的惯性矩 0 I 和等截面梁段 BC 的横截 面对中性轴 z 的惯性矩 2 I 分别为 12 3 0 0 b h I = , 12 3 2 2 b h I = (2) 由(1)式和(2)式可得 l a l b b I I − = = 2 0 2 0 (3) 对 AB 段(0≤ 1 x ≤a),梁在 1 x 截面处的宽度、对中性轴 z 的惯性矩和弯矩分 别为 ( ) ( ) l b l x b x 0 1 1 1 − = ( ) ( ) l l x I b x h I x 1 0 3 1 1 1 1 12 − = = ( ) ( ) 1 1 1 M x = −P l − x (4) 梁的挠曲线近似微分方程为 ( ) ( ) 1 1 0 1 1 1 EI Pl EI x M x y′′ = − = (5) 积分两次得到 1 1 0 1 x C EI Pl y′ = + 1 1 1 2 1 0 1 2 x C x D EI Pl y = + + (6) 利用边界条件 y1 () () 0 = y1 ′ 0 = 0,可以得到C1 = D1 = 0,故梁在 AB 段的挠曲线 方程和转角方程分别为

为微 4=州=品4 (7) 对BC段(a≤x2≤D,梁在x2截面处的弯矩为 M2k2)=-Pl-x2) 8 梁的挠曲线近似微分方程为 巧=-4,).p 0-) 积分两次得到 g0-+6 为0--c0-srn (10) 利用边界条件a)=a)、(a)=向)以及(3)式,可以得到 G_,o,-v-y-0- (11) 2E2 故梁在BC段的挠曲线方程为 为=,-P-t-ak-+-obw--arl (12) BC段的挠曲线方程也可用叠加法求解。B截面的挠度和转角分别为 =器 (13) 根据叠加法,有 =+a,6-o小+--o小--明 (14) 将(13)式代入上式,得到梁在BC段的挠曲线方程为 %-ds-fe-2a-w-oe-】 (15) 4.根据等强度梁的基本尺寸和加荷大小计算出有有关力学性能 基本尺寸: 跨度1=36cm 梁高h=1.2cm 梁宽度b=10.2cm梁的弹性模量E=3.0×10'g/cm2 荷载P=2g(注基本尺寸要求同学自己量出)
5 2 1 0 1 2 x EI Pl y = 1 0 1 1 x EI Pl θ = y′ = (7) 对 BC 段(a≤ 2 x ≤l),梁在 2 x 截面处的弯矩为 ( ) ( ) 2 2 2 M x = −P l − x (8) 梁的挠曲线近似微分方程为 ( ) ( ) 2 2 2 2 2 2 l x EI P EI M x y′′ = − = − (9) 积分两次得到 ( ) 2 2 2 2 2 2 l x C EI P y′ = − − + () () 2 2 2 3 2 2 2 6 l x C l x D EI P y = − − − + (10) 利用边界条件 y () () a y a 2 1 ′ = ′ 、 y (a) y (a) 2 = 1 以及(3)式,可以得到 ( ) 2 2 2 2 2EI P l a C − = , ( )[ ( ) ] 2 2 2 2 6 3 EI P l a l l a D − − − = (11) 故梁在 BC 段的挠曲线方程为 { } ( ) ( )( )( ) ( ) [ ] 2 2 2 3 2 2 2 2 2 3 3 6 l x l a l x l a l l a EI P y = − − − − + − − − (12) BC 段的挠曲线方程也可用叠加法求解。B 截面的挠度和转角分别为 ( ) 0 2 1 2EI Pla yB = y a = ( ) 0 1 EI Pla a θ B =θ = (13) 根据叠加法,有 ( ) ( ) ( )( ) x a [ ] l a x a EI P y y x a = B + B − + − − − 2 − 2 2 2 2 2 3 6 θ (14) 将(13)式代入上式,得到梁在 BC 段的挠曲线方程为 [ ] ( ) ( ) ( )( ) x a l a x a l a x a EI P y = − − − 2 + − 2 − 2 2 2 2 3 2 3 2 6 (15) 4.根据等强度梁的基本尺寸和加荷大小计算出有有关力学性能 基本尺寸: 跨度 l = 36cm 梁高 h = 1.2cm 梁宽度 b = 10.2cm 梁的弹性模量 4 2 E = 3.0×10 kg / cm 荷载 P = 2kg (注基本尺寸要求同学自己量出)