
K,dv=πe2Nof/mc (eq.8-4) 公式中:e为电子电荷;m为电子质量;c为光速; N,为单位体积内基态原子数;f振子强度,即能被入 射辐射激发的每个原子的平均电子数,它正比于原子对 特定波长辐射的吸收几率。表明:积分吸收值与单位原 子蒸气中吸收辐射的基态原子数呈简单的线性关系,这 是原子吸收光谱分析法的重要理论依据。 若能测定积分吸收,则可求出原子浓度。但是,测 定谱线宽度仅为10-3nm的积分吸收,需要分辨率非常高 的色散仪器,技术上很难实现。所以,1955年瓦尔西提 出采用锐线光源来解决求积分吸收值的难题。参见下图:
公式中: e为电子电荷;m为电子质量;c为光速; N0为单位体积内基态原子数;f 振子强度,即能被入 射辐射激发的每个原子的平均电子数,它正比于原子对 特定波长辐射的吸收几率。表明:积分吸收值与单位原 子蒸气中吸收辐射的基态原子数呈简单的线性关系,这 是原子吸收光谱分析法的重要理论依据。 若能测定积分吸收,则可求出原子浓度。但是,测 定谱线宽度仅为10-3nm的积分吸收,需要分辨率非常高 的色散仪器,技术上很难实现。所以,1955年瓦尔西提 出采用锐线光源来解决求积分吸收值的难题。参见下图: ∫K d = e 2N0ƒ/mc +∞ -∞ (eq.8-4)
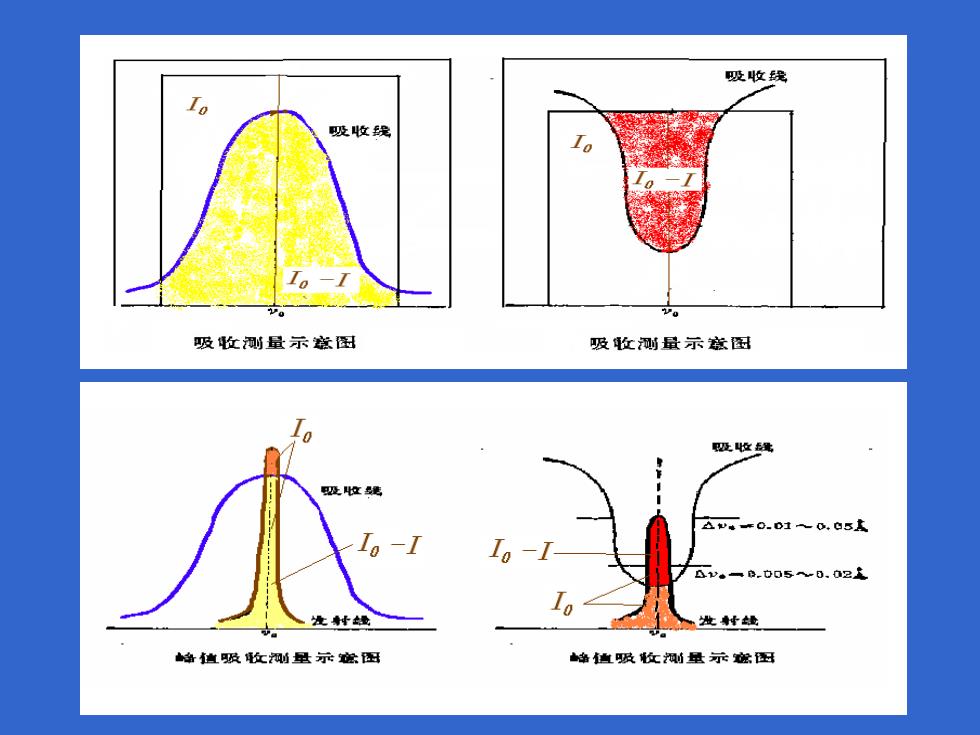
吸收线 10 吸收暖 吸收测量示滋团 吸收则量示兹团 吸收绳 吸收镜 e0.D10,5 0.D05b.021 峰做级收知则量示滋图 峰直吸收烟则量示途母

由图可见,在使用锐线光源时,光源发射 线半宽度很小,并且发射线与吸收线的中心频 率一致。这时峰值吸收系数Kv可认为是常数。 目前,一般采用测量峰值吸收系数的方法 代替测量积分吸收系数的方法,就不需要用高 分辨率的单色器,而只要简单分光,就能测出 峰值吸收系数,从而由郎伯-比尔定律可求出被 测物基态原子的浓度
由图可见,在使用锐线光源时,光源发射 线半宽度很小,并且发射线与吸收线的中心频 率一致。这时峰值吸收系数K可认为是常数。 目前,一般采用测量峰值吸收系数的方法 代替测量积分吸收系数的方法,就不需要用高 分辨率的单色器,而只要简单分光,就能测出 峰值吸收系数,从而由郎伯-比尔定律可求出被 测物基态原子的浓度

五、原子吸收定量公式的推导 若以I。和I分别代表光源通过原子蒸气 前后的总光强度: A=1g-I 6=∫ovdv I=dv 由郎伯-比尔定律,=vekL,I=ved dv A=1g
五、原子吸收定量公式的推导 若以 I0 和 I 分别代表光源通过原子蒸气 前后的总光强度: A = lg I0 I I = I ∫ d e 0 I0 = I ∫ 0 d e 0 由郎伯-比尔定律 Iν = I0 e -KL , I = I0 e -KL ∫ d e 0 A = lg I ∫ 0 d e 0 I0 e -KL ∫ d e 0

对锐线光源,可以认为K,=K,为常数: A=1g1,=1geKL=0.4343KL e-KoL K值与谱线的宽度有关,在通常原子吸收分析的条 件下,若吸收线轮廓单纯取决于多普勒变宽,则 Ko= .e'Nof (eq.8-5 △yD mc A=0.4343× 21n2 .e NofL △yD mc
对锐线光源,可以认为Kν= K0 为常数: A = lg = lg eK0L 1 = 0.4343K0L e -K0 L K0值与谱线的宽度有关,在通常原子吸收分析的条 件下,若吸收线轮廓单纯取决于多普勒变宽,则 (eq.8-5)