
第二章人工神经网络的基本模型 2.1人工神经元的基本模型 对M-P人工神经元进行改进的主要方式有如下几个方面: ■神经元的内部改造:对人工神经元取不同的非线性函 数; 对输入和输出做不同的限制:离散的(某些离散点) 和连续的(整个实数域)。 ■神经网络的结构上的改造:人工神经元之间的联接形 式不同。 ■算法的改进:在人工神经网络权值和阈值取求的方法 上不同。 其它形式的改造。 2006-5-9 北京科技大学自动化系 12
2006-5-9 北京科技大学自动化系 12 2.1 人工神经元的基本模型 第二章 人工神经网络的基本模型 对M-P人工神经元进行改进的主要方式有如下几个方面: 神经元的内部改造:对人工神经元取不同的非线性函 数; 对输入和输出做不同的限制:离散的(某些离散点) 和连续的(整个实数域)。 神经网络的结构上的改造:人工神经元之间的联接形 式不同。 算法的改进:在人工神经网络权值和阈值取求的方法 上 不同。 其它形式的改造
第二章人工神经网络的基本模型 2.2几种典型的激活函数(Activation Function) 激活函数一执行对该神经元所获得的网络输入的变 换,也常称为激励函数、活化函数:o=f(net) 线性函数(Liner Function) f(net)=k*net+c 0 net 2006-5-9 北京科技大学自动化系 13
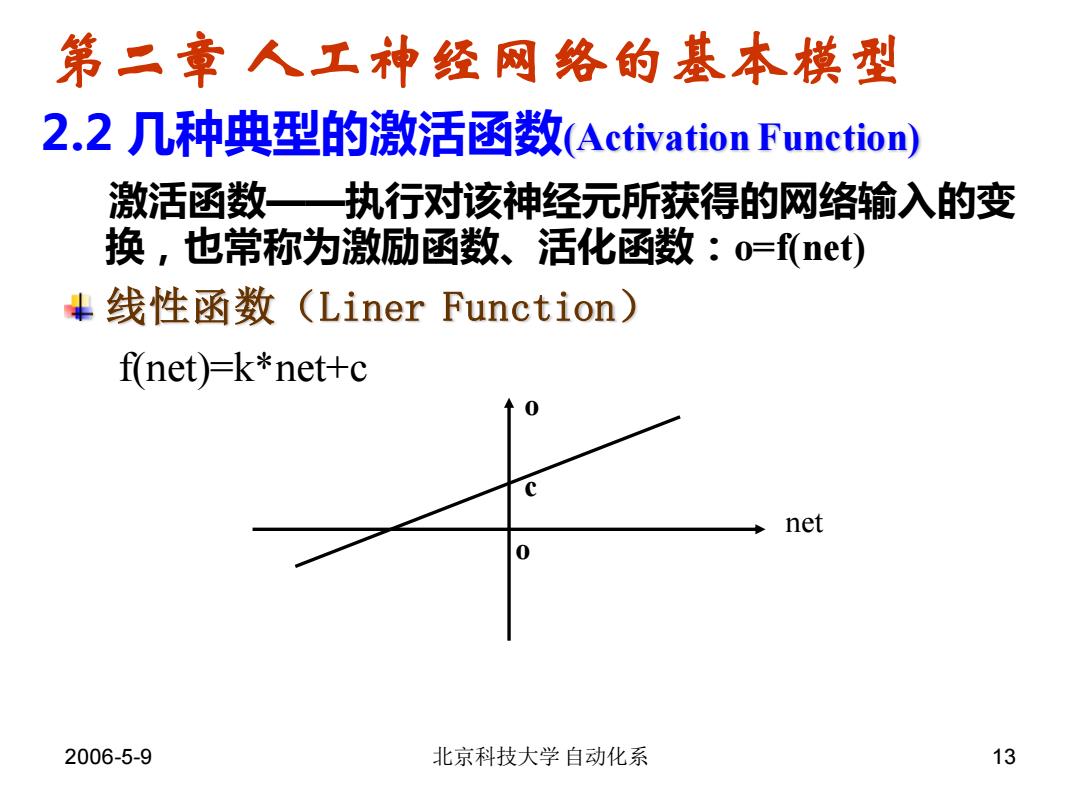
2006-5-9 北京科技大学自动化系 13 激活函数——执行对该神经元所获得的网络输入的变 换,也常称为激励函数、活化函数:o=f(net) 线性函数(Liner Function) f(net)=k*net+c net o o c 2.2 几种典型的激活函数(Activation Function) 第二章 人工神经网络的基本模型

第二章人工神经网络的基本模型 2.2几种典型的激活函数(Activation Function) 2、非线性斜面函数(Ramp Function). y if net0 f (net)=k*net i if net<0 if net<-0 >0为一常数,被称为饱和值, 为该神经元的最大输出。 Y 0 net -Y 2006-5-9 北京科技大学自动化系 14
2006-5-9 北京科技大学自动化系 14 2、非线性斜面函数(Ramp Function) γ if net≥θ f(net)= k*net if |net|<θ -γ if net≤ -θ γ>0为一常数,被称为饱和值, 为该神经元的最大输出。 γ -γ -θ θ net o 2.2 几种典型的激活函数(Activation Function) 第二章 人工神经网络的基本模型

第二章人工神经网络的基本模型 2.2几种典型的激活函数(Activation Function) 阈值函数(Threshold Function)阶跃函数 if net0 if net<0 y0均为非负实数,0为阈值。 二值形式: if net-0 if net< net 双极形式: fine)- if net-0 if net0 2006-5-9 北京科技大学自动化系 15
2006-5-9 北京科技大学自动化系 15 β if net>θ f(net)= -γ if net≤θ βγθ均为非负实数,θ为阈值。 二值形式: 1 if net>θ f(net)= 0 if net≤θ 双极形式: 1 if net>θ f(net)= -1 if net≤θ β -γ θ o net 0 2.2 几种典型的激活函数(Activation Function) 第二章 人工神经网络的基本模型 阈值函数(Threshold Function)阶跃函数
第二章人工神经网络的基本模型 2.2几种典型的激活函数(Activation Function) 其他形式的作用函数:不同的作用函数,可构成不同的神经 元模型 非对称型Sigmoid函数:简称S型作用函数,是可微的,用下式表示: 如图(a)和(b) 1 f(x)= I+e-x 或 f(x)= 1+e B>0 9 0.9 0.8 01 7 0.6 0.6 &05 0,5 04 04 0.3 0.3 03 0.1 01 -6 -4 -2 (a) -6 (b) 图2-2-3 (a)B=1 (b) ”三2 2006-5-9 北京科技大学自动化系 16
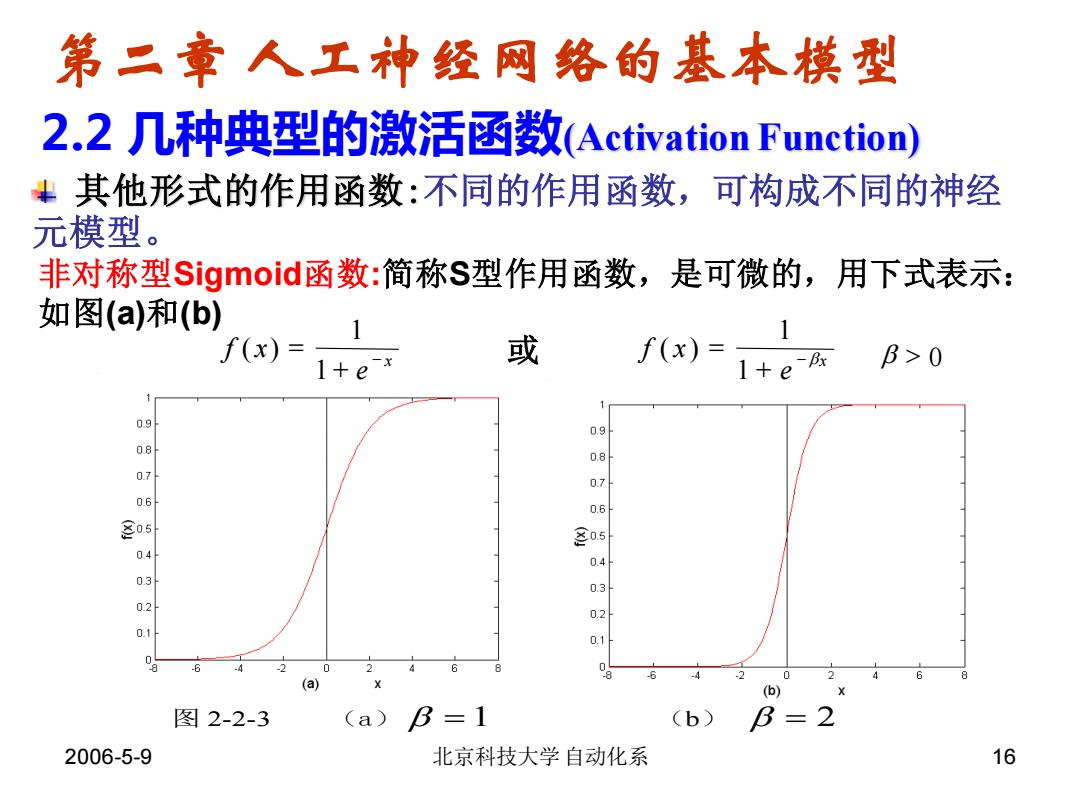
2006-5-9 北京科技大学自动化系 16 2.2 几种典型的激活函数(Activation Function) 第二章 人工神经网络的基本模型 其他形式的作用函数:不同的作用函数,可构成不同的神经 元模型。 图 2-2-3 (a) = 1 (b) = 2 非对称型Sigmoid函数:简称S型作用函数,是可微的,用下式表示: 如图(a)和(b) f x e x ( ) = + − 1 1 或 f x e x ( ) = + − 1 1 > 0