
第1章量子理论导论 量子力学描述原子或分子中电子运动状态的量子力学方法可归纳如下: (I)通过写出体系的正确的势能函数V,写出Schrodinger方程。 (2)解出描述电子运动的Schrodinger方程,得到电子的能量E,及波函数4,i=1,2,. (3)给出第i态的儿率密度函数4?及其他物理性质的数值。 通过体系的Schrodinger方程,可得体系的总能量和波函数。如上节所述,从波函数又可 得体系所处状态的各种物理量值。体系的能量是体系的重要性质,它有总能量E,动能T和 势能V等内容。根据已知的H原子基态的波函数4[见式(1.3.6)]及量子力学的算符,就可 以得到这些数值: 总能量值E,: =[禁点, (1.4.14) 即可推得 =(专)-2.18x10J-16ev (1.4.15) 平均势能〈V)也能容易算得 v)sinedo (ma)exp)exp-r e =一4re0a0 (1.4.16) 平均动能〈T)可从E,和(V)的差值算得 D=E-W-点,云 (1.4.17) 由计算可知,平均动能(T)和总能量E数值相等,符号相反: E=-〈T)=(W) (1.4.18) 这个关系式适用于由核和电子组成的原子和分子体系,即当在最低能量时,吸引力和排斥力均 正比于1/。方程(1.4.l8)是适用于原子和分子体系的维里定理(virial theorem)。 下面一节将处理几个量子力学的体系,以阐明这里所介绍的方法。 l.5 Schrodinger方程的简单应用 在这一节中,将用量子力学处理一些简单的体系。在本节所给的几个例子中,粒子(即电 子)都允许自由地运动,差别在于容器(即箱子)的形状。由于形状不同,边界条件不同,就有不 同的能量(或称本征值)和不同的波函数(或称本征函数)。 1.5.1一维箱中粒子 这个体系在一般的物理化学和结构化学基础中都有介绍,在这里列出,温故知新,更好地 和后面例子进行对比讨论。 在此体系中,箱子是一维(只有长度)的,长度为。在箱中势能为0,在边界上和边界以外 势能为无穷大。 仅限读者PB18030910本人使用,阅毕请除 不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

10 第I部分化学键理论基础 (1.5.1) 此体系的Schrodinger方程为 (1.5.2) 学 票中=-8v=- (1.5.3) 其中 a2=8π2mE/h (1.5.4) 解方程(1.5.3),得 (x)=A sinaz-十B cosa.z (1.5.5) 式中A和B是常数,要根据(1.5.1)式给出的边界条件来定 在x=0和x=a处,势能无穷大。因此在这两点及其附近不可能找到微粒,即 (0)=(a)=0 (1.5.6) 由(0)=0,得 B=0 (1.5.7) 由(a)=0,得 A sinaz=0 (1.5.8) 这说明A或sinax至少有一个为0。由于B=0,若A再为0,整个(1.5.5)式即波函数为0,没 有意义,不能接受。所以 sinax=0 (1.5.9) ax=n,n=1,2,3,. (1.5.10) 由此得波函数: ,(x)=Asin”Z,n=1,2,3, (1.5.11) 常数A可由归一化定出: ∫14Pd=Asindr=1 (1.5.12) 由此得到:A=√②/a。所以完整的波函数为 a)aang,n=12,3. (1.5.13) 注意:中的单位为(长度)2,的单位为(长度)1。 除波函数外,体系的能量也已定出。将(1.5.4)式和(1.5.10)式结合起来,得 √ (1.5.14) 或者 E=82,n=1,23. (1.5.15) 图1.5.1示出一维箱中粒子的波函数、几率密度和E。等图形和数据。从图1.5.1可以看 到,电子在基态时(n=1)最容易在箱子中心找到它。另外,若它处在第一激发态(n=2),则在 x=a/4和x=3a/4附近最容易找到它。 下面以基态4为例,计算其平均动量(p)及平均动量平方(): 仅限读者PB18Q30910本人使用,阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播
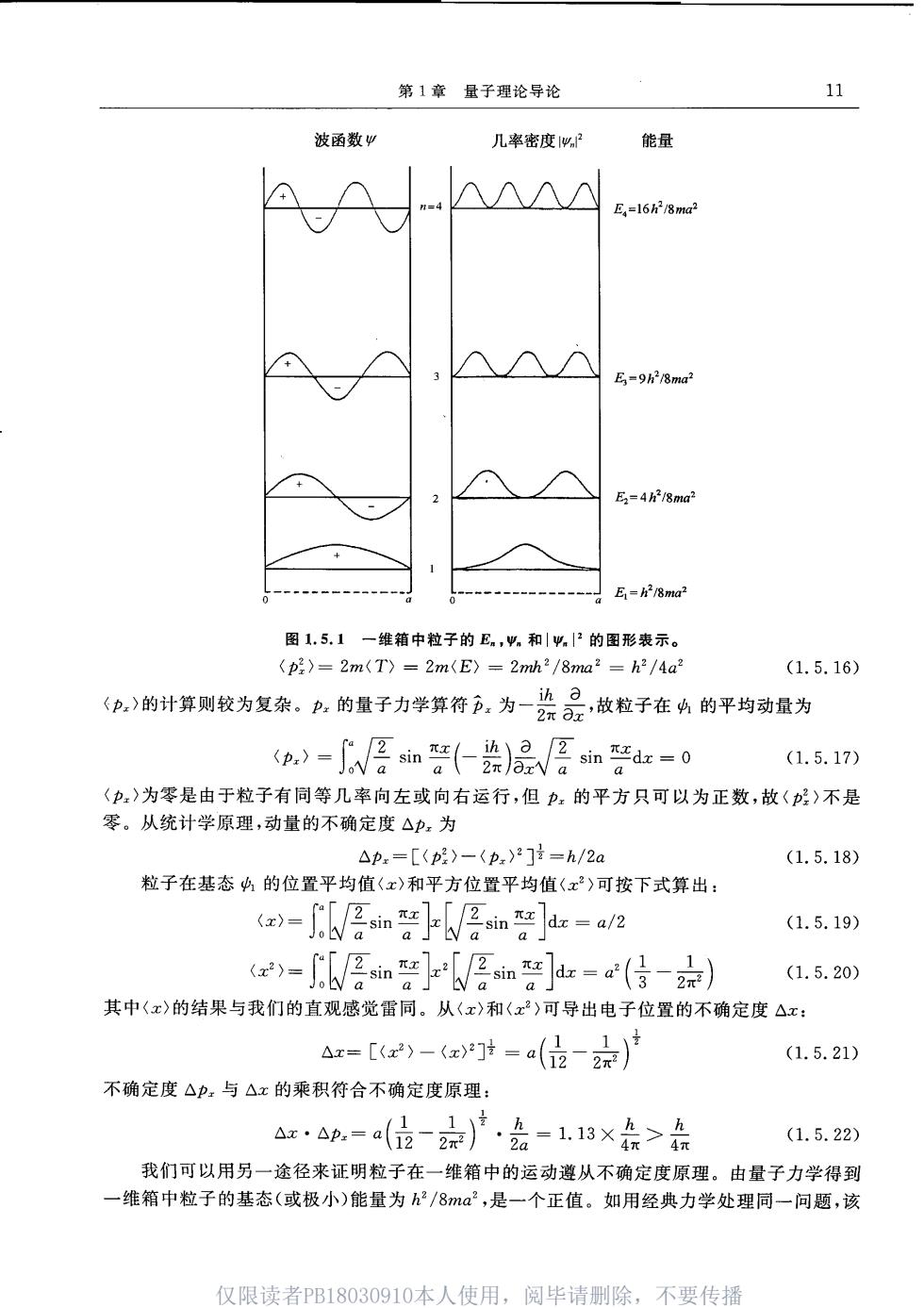
第1章量子理论导论 11 波函数 几率密度g2 能量 A个∧N E,=168m E=9h8ma? E=4/8ma2 -E=28m2 图1.5.1一维箱中粒子的E,和.的图形表示。 〈p2》=2m(T)=2m(E〉=2mh2/8ma2=h2/4a2 (1.5.16) (p.)的计算则较为复杂。P,的量子力学算符户,为一染是,故粒子在4的平均动量为 p-∫N悟血(2)品层如=o (1.5.17) 〈p)为零是由于粒子有同等几率向左或向右运行,但力,的平方只可以为正数,故(》不是 零。从统计学原理,动量的不确定度△p,为 △p.=[(p)-(p,)2]量=h/2a (1.5.18) 粒子在基态4的位置平均值(x)和平方位置平均值(x)可按下式算出: ()-Jsinsindr -al2 (1.5.19) ()-Shsin sindr-a() (1.5.20) 其中〈x)的结果与我们的直观感觉雷同。从(x)和〈x2)可导出电子位置的不确定度△x: =【)-at=a(位-)月 (1.5.21) 不确定度△p,与△x的乘积符合不确定度原理: axap-a(位-京)产,会-118×会>点 (1.5.22) 我们可以用另一途径来证明粒子在一维箱中的运动遵从不确定度原理。由量子力学得到 一维箱中粒子的基态(或极小)能量为h/8ma2,是一个正值。如用经典力学处理同一问题,该 仅限读者PB18030910本人使用,阅毕请别除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

12 第I部分化学能理论基础 能量应为零。两种方法得到的能量之差可以被看成是零点能。零点能的存在意味着在量子力 学中受束缚粒子的动能及动量均不为零。如果我们把基态能量表示为p/2m,那么粒子的动 量极小值为士h/2a。因此,其不确定量△p.为h/a:假设位置不确定量△x为箱子的长度a,那 么△x△p,为h。这和不确定度原理是一致的。 一维箱中粒子用量子力学处理所得的结果能用来描述共轭多烯分子中的离域元电子,这 种近似称为自由电子模型。以丁二烯分子为例,分子中的4个π电子应处在4和4轨道,给 出(4)(4)2组态。若将一个电子从么轨道激发到4轨道,需要的能量是 △E=5h2/8ma2=hc/a (1.5.23 箱子的长度a可近似估算如下:典型的C一C和C一C键长为154pm和135pm,若允许π电 子的运动超出端基碳原子一点,如约70pm,箱子的长度为560pm,即作为a的数值,按 (1.5.23)式,可算得入为207.0nm,实验测定丁二烯吸收光的波长为210.0nm。所以这虽然 是一个粗略模型,其结果却意外地好。 1.5.2三维箱中粒子 三维箱的势能函数可表达为 V=0,0<a和0<y<b和0<<c ,x≥a,x≤0和y≥b,y≤0和名≥c,2≤0 (1.5.24) 它的Schrodinger方程为 (1.5.25) 为了解此方程,需要进行变数分离,令 (xy,z)=X(x)Y(y)Z(s) (1.5.26) 将方程(1.5.26)代人(1.5.25),可得 v-(景++是)vz-8xz (1.5.27) Yz8x+Xz影+Xy2=-8mxYz (1.5.28) 将(1.5.28)式两边用XYZ除,得 )+器+()- (1.5.29) 很明显,(1.5.29)式左边的三项每一项都应等于常数,即 X =-0i (1.5.30) 器-叫 (1.5.31) 2影=-心 (1.5.32) 而这三个常数之和应受下式限制: g+听+a-8rmE (1.5.33) 仅限读者PB18030910本人使用,阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

第1章量子理论导论 13 由此式可看出,每个自由度在总能量上都有它自已的贡献,可写成 8mE omE 2 h2 h (1.5.34) E=E,+E,+E. (1.5.35) 方程1.5.30)~(1.5.32)中的每一个式都和一维箱的方程(1.5.2)或(1.5.3)相似,因而方程 (1.5.30)~(1.5.32)的解就可以立即写出于下: X,()=√sin%,%=1,2,3. (1.5.36) ,)-层m2,%=1.2,3 (1.5.37) 乙,(a=√sin =1,2,3,. (1.5.38) 总的波函数如方程(1.5.26)的形式则成为 4(z,y,)-√及sin"sinin% (1.5.39) 这里中的单位为(体积)一,心的单位为(体积)1,为三维箱体系的几率密度函数。 如同波函数决定于量子数,体系的能量也和三个量子数相关: En=(E,+(E,+(E入=(倍+器+) n,n,n,=1,2,3, (1.5.40) 如果势箱为一立方体,即a=b=c,则方程(1.5.40)变为 =优++》,%%=1,23 (1.5.41) 方程(1.5.41)对不同状态能量表达式有一个有趣的特点,即一组具有不同量子数和不同的波 函数,可能有着相同的能量。当不同的状态有着相同的能量,它们被称为简并态。例如: E1.1.李=E1.9.1=E21.1=6h2/8ma2 (1.5.42) 注意42,4,21,4,1是不同的波函数,但是它们的能量相同,都为6h/8ma2。同样: E1.2.3=E8.1,3=E1.3.9=E3.L.2=E3.3.1=E2a.1=14h2/81a2 (1.5.43) 下面用三维箱中粒子模型了解色中心问题。当钠蒸气通过NCl品体后,晶体会呈现黄 绿色,它是由下一过程所产生: 8Na(g)+NaCl(c) →(Na*)1+(CIe)(c),61 在此“固态反应”中,被吸附的Na原子在晶体表面 -Na 上电离,过多的电子扩散进入晶体内部并占据负离 子位置的空位,同时等量的C一移向晶体表面,保持 电中性。占据负离子空位的囚禁电子称为色中心或 F-中心(F来源于德文的颜色Farbe)。图1,5.2示 出在(Na+)1+(CIe)晶体中的一个囚禁电子。在 这实验中观察到的颜色与箱中粒子在两个能级间的 ○ 跃迁有关。在定量地处理这个问题之前,可以饶有国1,5,2在卤化钠晶体中的色心(e标记) 兴趣地注意到不同的颜色是和主体晶体的性质有[注意电子的位置是一个卤离子X的位置 关,而和电子的来源无关。例如在钾蒸气中加热(已空缺),为清楚起见X设有表示出来门 仅限读者PB18030910本人使用, 阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播