
4 第I部分化学键理论基础 不确定度原理就不可能说一个已知具有准确速度的电子是准确地在某一点上。必须强调这里 所讨论的不确定性并不涉及所用的测量仪器的不完整性,它们是内在固有的不可测定性。N. Bhr(玻尔)为氢原子所提的理论中电子的位置和速度都可精确计算,说明他的模型违反了不 确定度原理。所以不能将Boh提出的电子按确定轨道绕原子核运动的原子结构模型推广应 在原子的水平上接受承认了不确定度,就要强调儿率:即在某体积元中找到电子的几率是 多少百分数以及它可能具有的速度或动量等。 1.3电子的波函数和几率密度函数 因为电子有波动特征,要用一个波动方程来描述它的运动,就像在经典力学中用来描述水 波、弹簧或鼓(膜)的运动一样。如果是一维体系,经典的波动方程为 (1.3.1) 式中~是波的传播速度,波函数Φ是在x点和时刻波的位移。在三维空间中,波动方程变 为 (景+品+是)0-o0 (1.3.2) 一个典型的波函数或波动方程的解,是已知的sin或cos函数,例如: (,t)=Asin (z-vt) (1.3.3) 可以容易地证明函数p(x,)满足方程(1.3.1)。必须记住一点,在经典力学中波函数是一个 振幅的函数:在量子力学中,电子的波函数却有着完全不相同的含义。 按实物粒子波的本性和不确定度原理的几率概念,M.Bor(玻恩)假定粒子的波函数已不 再是振幅的函数,取代它的是粒子出现的几率。当这个波函数的绝对值越大,粒子出现的儿率 也就越大。下面给出这种几率的一个例子。 从不确定度原理人们已不再说一个电子的准确位置。反之,只可用几率密度函数来定义 电子的位置。将几率密度函数用(x,y,z)表示,那么可说电子是在P具有最大值的区域。实 际上,p(,y,)d是电子在(x,y,)点附近的微体积dr(drdyd)中出现的几率。注意,p的 单位是(体积)1,而dx则是儿率,它没有单位。如果用不含时间的定态波函数(x,y,x)代 表,Bon假定的几率密度函数P则是中的绝对值的平方: p(x,y,z)=(x,y,g)|2 (1.3.4) 因为中有时是虚数,为了保证·为正值,当中为虚数时,则以共轭复数相乘: |(x,y,z)|2=(x,y,z)x,y,z) (1.3.5) 式中(x,y,z)是(x,y,2)的共轭复数,即将(x,y,2)中的i用-i置换。 用波函数描述具有波性的粒子的行为,是量子力学提出的第一个重要假设。将波函数和 微粒出现的几率密度相联系,表达微粒运动的情况,是解决测量具有波粒二象性体系的性质的 关键。当得到体系所处状态的波函数中和儿率密度=(2),有关该体系的许多问题,就可 仅限读者PR18030910本人使用、阅请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

第1章量子理论导论 以得到解决,下面结合一个实例进行讨论。 对于一个氢原子,其基态的波函数为 4-(a)cn[] (1.3.6) 式中r是电子离核的距离,a的数值为52.9pm,是氢原子的第一个Bohr轨道的半径。a。称 为Bohr半径。下面按波函数4作一些计算: (1)求算在离核为52.9pm(即ao)的空间某一点上:①4.的数值,②电子出现的几率密 度p,③在1pm体积中电子出现的几率P。 [x52.9pm]f×0.368=5.39x10-pmn 1 ②p=4.=|4.|2=[5.4×10-4pm-]2=2.91X10-1pm3 ③在空间该点附近1pm3体积中电子出现的几率: P=|4,dr=(2.91X10-1pm)X(1pm3)=2.91X10 (2)求算电子离核为52.9pm处,厚度为1pm的球壳中电子出现的儿率。 解:球壳的体积(V)=球面积×球壳厚度=4π2·△r =4π×(52.9pm)2X(1pm)=3.52X10pm2 P=|42×V=(2.91×10-7pm3)×(3.52×10pm3)=1.02×10- 即电子在离核为a处,厚度为1pm球壳中出现的几率约为1%. 根据上述计算,可获得氢原子的电子处在基态(即15态)离核距离()不同时波函数4, 值、几率密度14,|2、lpm3体积(即dx=1pm)中的几率P(=4,2dx),以及厚度为1pm的球 壳中的几率4x2听,dr,列于表1.3.1中。 表1,3.1氯原子1s态不同r值的,2,1pm2体积中的几率(P) 和离核为rpm球壳中的几率(4r2呢dr,dr=lpm) r/pm 0 26.45(即2)) 52.9(即ao) 100 200 %./pm量 1.47×10- 8.89×10 5.39×10-4 2.21×10- 3.34×10-3 14,产/pm8 2.15×10-6 7.91×10-7 2.g1×10- 4.90×10-8 1.12×10-9 p 2.15×10-6 7.91×10- 2.91×10-7 4.90×10-9 1.12×10- 4π产吃,dr 0 6.95×10-3 1.02×10-2 6.16×10-3 5.62×10-4 中~x代表在一确定位置上体积为dx的空间中发现电子的几率,而电子全部几率总和为 1,中必须满足下一关系: 中dr=1 (1.3.7) 此时,中称为归一化了。另一方面,若中π=N,其中N为一常数,则N立中为一个归一化 的波函数,N士称为归一化常数。 通常的情况是:一个给定的体系会有无限数目可接受的波函数4,4,.,4,.,这些 仅限读者PB18030910本人使用,阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

6 第I部分化学键理论基础 波函数相互间为“正交的”,即 4中dr=鸣中,dr=0 (1.3.8) 结合归一化的条件[方程(1.3.7)]和正交的条件[方程(1.3.8)门,得到波函数间正交归一的关系: =时-4-侣 (1.3.9) 在方程(1.3.9)中,d,称为Kronecker delta函数。因为2已是几率密度函数,中必须是有限 的、连续的和单值的。 波函数在量子力学中起了核心的作用。波函数展示出原子和分子中电子的运动状态,是 探讨化学键理论的重要基础。通常称在原子中的电子分布的波函数为原子轨道(atomic or- bital,.AO),称分子中电子分布的波函数为分子轨道(molecular orbital,MO)。 当知道原子中的电子在各种状态时(如1s,2s,2p,3s,3p,3d,.)的中表达式,就可计算出 各状态的中在空间各处的大小和正、负值,并画出图形表示。图1.3.1(a)左边为,r关系曲 线图,右边为r为某一定值时,4:的圆球形等值面,即通常表达的原子轨道轮廓图。图 1.3.1(b)示出几率密度哈,和4π产片,对r的关系图。由于几率密度反映原子中电子分布情况 故又称为电子云。电子云的大小可用小黑点的稀密形象地表示,所以在图1,3.1(b)的右边形 象地表达听,的分布,即电子云图。它表明1s轨道在核附近有最大的儿率密度,离核距离加 大,密度稳定下降。 波函数不仅可表达出体系的图像,还可计算体系在波函数所代表状态可观察到的物理量 A。在量子力学中,A有着相应的线性自轭算符A算符是一个函数转变为另一个函数的运算 规则。当A作用于中满足下一关系时: A妙=a妙 (1.3.10) 波函数中称为算符A的本征函数,a称为中状态下物理量A的本征值。下节讨论的 Schrodinger方程: ip=E沙 (1.3.11) 就是通过它可以求出能量E和中的重要方程。 若物理量算符A对体系波函数中的作用不能满足(1.3.10)式,即得不到常数α乘中,则可 以通过下式求A的期望值(或平均值)(A): 〈A)=中Apdrod (1.3.12) 若少已归一化,方程(1.3.12)成为 (A)=Aodr (1.3.13) 例如,氢原子中的电子在1s态时并没有确定位置,即没有本征值。这时可按(1.3.13)式求平 均值。由于r的算符就是r,而对球型函数而言,dr=4π2d,代人(1.3.13)式得 r=i4rd=are即[-]4rd (1.3.14) 仅限读者PB18030910本人使用,阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播
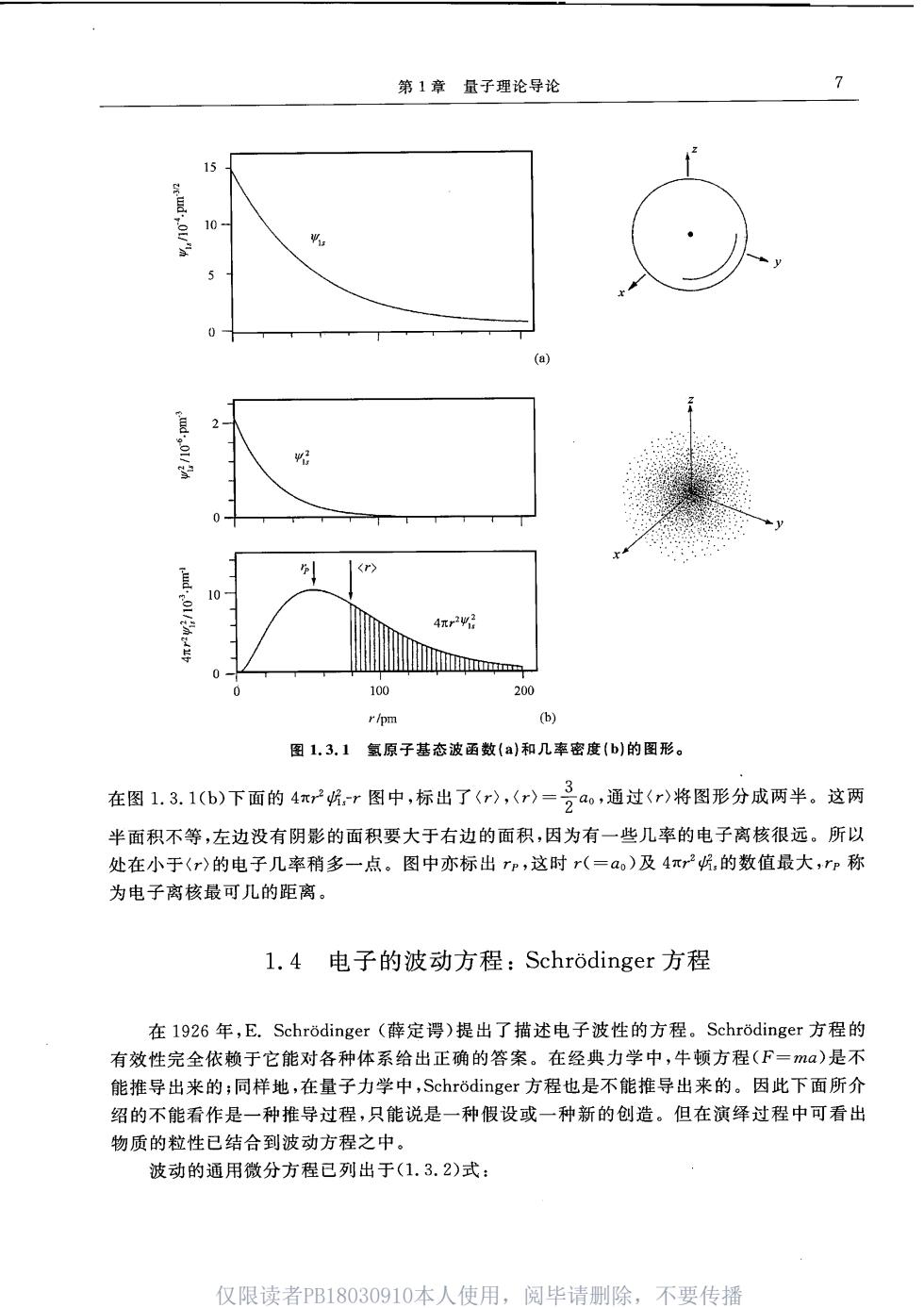
第1章量子理论导论 10= 0 色 0- 4xrv 100 200 r/pm 图1,3,1氢原子基态波函数(a)和几率密度(b)的图形。 在图1.3.1(b)下面的4r(r图中,标出了(),()=号a,通过r)将图形分成两半。这两 半面积不等,左边没有阴影的面积要大于右边的面积,因为有一些几率的电子离核很远。所以 处在小于〈r)的电子几率稍多一点。图中亦标出rP,这时r(=a)及4π2吮,的数值最大,rp称 为电子离核最可儿的距离。 l.4电子的波动方程:Schrodinger方程 在1926年,E.Schrodinger(薛定谔)提出了描述电子波性的方程。Schrodinger方程的 有效性完全依赖于它能对各种体系给出正确的答案。在经典力学中,牛顿方程(F=ma)是不 能推导出米的;同样地,在量子力学中,Schr心dinger方程也是不能推导出来的。因此下面所介 绍的不能看作是一种推导过程,只能说是一种假设或一种新的创造。但在演绎过程中可看出 物质的粒性已结合到波动方程之中。 波动的通用微分方程已列出于(1.3.2)式: 仅限读者PB18030910本人使用,阅毕请别除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

第I部分化学键理论基础 0zy,0)=是g0 (1.3.2) 其中波函数Φ有一个时间:的变数,因为体系的能量是和时间有关的。对一个不含时间变数 的方程,亦即和时间无关的波动方程,可用以描述定态波或驻波(此处不考虑辐射过程)。为了 获得和时间无关的方程,假定(x,y之,)具有下面形式: (x,y,2,)=(x,y,2)·g() (1.4.1) 式中(x,y,z)是空间坐标的函数,g(t)是时间t的函数。对于驻波,有几种可采用的函数,其 中之一是 g(t)=exp[2xiu] (1.4.2) 式中频率是和传播速度v及波长入有关: y=v/λ (1.4.3) 将(1.4.2)式代人(1.4.1)式,得 Φ=中exp[2πiw] (1.4.4) 将(1.4.4)式代人(1.3.2)式,得 ep[2i].o=子exp[2ai exptzrivle (1.4.5) 消去exp[2πi],得 中=-4 (1.4.6) 2 将入=/p波粒关系的方程代入 =v=v(h/p)=hv/p (1.4.7) 这样,方程(1.4.6)变为 4-4np中 (1.4.8) 将2用动能T、总能量E和势能V表达,即 p*2mT =2m(E-V) (1.4.9) 得波动方程: 中=-8元m(E-)沙 (1.4.10) 或重排为 [+v= (1.4.11) 或写成 Hy=Ey (1.4.12) 其中 庄=-gn+v (1.4.13) 方程(1.4.11)称为Schrodinger方程,是适用于电子波动的方程,这个方程的缩写形式为 (1.4.12)式,式中产称为Hamilton算符。从方程(1.4.13)可看出户分为两部分:动能算符 一8n和势能算符V. 仅限读者PB18030910本人使用,阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播