
12 高等无机结构化学(第2版) 参考文献 .(568) 第18章稀土元素的结构化学.(570) 18.1稀士元素的性质 .(570) 18.1,1余属原子半径和离子半径的变化趋势:拥系救缩.·(571) 18.1.2稀土金属的品体结构. (571 18.1.3氧化态. (572) 18.1.4 光谱项和电子光谱. ***(573 18.1.5性. (574) 18.2稀土元素氧化物和卤化物的结构. ****.(574 18.2.1化扬+44(574) 18.2.2卤化物. (575) 18.3稀土离子的配位几何学. 18.4稀士元素的有机金属化合物. (580) 18.41 环戊二烯基稀土配合物· (580) 18.4.2苯和环辛四烯基稀土配合物. (582) 18.4.3带有其他有机配位体的稀土配合物.(582) 参考文献. 第19章 金属-金属键和过渡金属簇合物. .(585) 19.1过渡金属簇合物的键价和键数.(585) 19.2含金属-金属键的二核过渡金属配合物.(588) 19.2.1 合18电子规则的二核过渡金属配合物 (588) 19.2.2 二核金属配合物中的四重键. (589) 19.2.3二核配合物中金属金属能的键价 (592) 19.2.4 二核金属配合物中的五重键.(594) 19.3三核和四核过渡金属簇合物 (595) 19.3.1三拉过渡金层簇合物.44.(595) 19.3.2四核过渡金属簇合物 (595) 19.4四核以上时渡金屈筏合物.,+. (596) 19.4.1五核过渡金属簇合物 . (596) 19.4.2六核过渡金属墓合物 .(597) 19.4.3六核以上过渡金属簇合物 (598) 19.5等同键价和等同结构系列.(599) 19.6金属金属相互作用研究选论 (602) 19.6.1亲金作用.: 19.6.2 亲银作用和混合金属配合物 (604) 19.6.3金属线分子.(604) 19.6.4含全属-金属的第12族低价化合物. (609) 仅限诗老PB18030910本人.使用、阁毕请别除, 不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

录 13 参考文献.(609) 第20章超分子结构化学 (611) 20.1引言 (611) 20.1.1分子间的相互作用.(611) 20.1.2分子识别 (611) 20.1.3自组装.(612) 20.1.4晶体工程 (614) 20.1.5超分子合成子.(615) 20.2氢键引导的组装 .(617) 20.2.1基于羧酸二聚体合成子的超分子的结构.(617) 20.2.2氢健式样的困形编码 .(619》 20.2.3基于杂环间氢能互补性的超分子结构.。 .(620) 20.2.4呈现玫瑰花形的氢键网络. (621 20.3配位键的超分子化学. .(627) 20.3.1 超分子的主要类型. (627) 20.3.2 一些有代表性的超分子例子. .·(627) 20.33无机超分子和配位高聚物的合成谋略. (631) 20.3.4分子多边形体和分子管. +(633) 20.3.5分子多面体. (635) 20.4品体工程的实例.。 .(640) 20.4.1金刚石型网络. .(640 20.4.2由南瓜尼构成的转子结构.(643) 20.4.3利用键的无机晶体工程. .(647) 20.4.4在尿素/硫脲络合物中不稳定的无机/有机负 离子的生成和稳定化.*.*.(648) 20.4.5 Ag(I)多面体与包藏其中的C经的超分子自组装.(655) 20.4.6含苯三酚[4]芳烃大环的纳米胶囊的自组装.(661) 20.4,7多孔金属-有机物骨架网络结构的设计和合成.(662) 20.4.8填充的碳纳米管.(668》 参考文献. (670) 索引. (672) 仅限读者PB18030910本人使用,阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

第I部分 化学键理论基础 化学键理论在快速发展的无机结构化学领域起着重要的作用。它帮助我们去了解各类化 合物的结构、性质和反应性能。经常可以发现化学键理论在无机结构化学的各种研究课题中 当作指导方针,包括合成路线的设计、分子和晶体中原子的空间排列、尚待制备的化合物的预 期性质等等。 这部分内容分为五章:量子理论导论、原子的电子结构、分子中的共价键、凝聚相中的化 学键以及计算化学。因为这些章中的部分内容已包括在物理化学、量子化学和结构化学教科 书之中,可以有把握地假设本书的大多数读者已对这里的一些内容有了一定的了解,所以在这 部分具体内容的取舍上,不同于大学基础课的结构化学和物理化学,也不同于专门的量子化学 课。主要是以提要的形式,归纳和复习结构化学的基础;以直述代替推论,介绍和引用化学键 理论的新成果和新进展。 仅限读者PB18O30910本人使用,阅毕请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播

第1章量子理论导论 为了全面地理解原子和分子的结构以及化学键理论,需要学习量子理论基础。虽然化学 是一门实验科学,但是现在高功能的计算科学的发展,使量子力学所起作用的重婴性日益增 加。将量子力学方法用于解决化学问题通称量子化学。 理论化学的关键是分子的量子力学,它处理分子水平上能量的转移或转化的问题。虽然 量子力学原理对于了解物质的电子结构从上世纪30年代起就已认识,而其应用的数学,对分 子体系的Schrodinger方程的通解,五十年来仍是难以对付的。但是随着新的理论和计算方 法的稳定发展,以及近二十年来价格合理的、更大的和更快速的计算机投入运算,使计算工作 几乎和实验工作的准确性相当,或者其准确性至少足够为实验工作者所利用,而计算工作比实 验工作的耗资少、耗时短,亦较容易控制。计算所得的成果常常用以引导实验化学家去合成或 发现新的分子、去解释他们在实验室中所得到的结果。所以量子化学在化学的各个分支中的 作用也显得日益重要:物理化学中用量子力学计算气体的嫡、热焓等热力学函数,解释分子光 谱,计算化学反应中过渡态的性质,了解分子间的作用力等:有机化学家用量子力学估计分子 的相对稳定性,计算反应中间物的性质,研究化学反应的机理:分析化学家用量子力学了解谱 线的频率和强度;无机化学家按量子力学的方法用配位场理论解释过渡金属配位化合物的性 质等。总之,化学已离不开量子理论所起的指导作用。l998年诺贝尔化学奖授予W.Koh和 J.A.Pople,以表彰他们对量子化学发展的贡献,也是科学界对量子化学的作用在增长的标 志。在第5章将扼要地描述各类由计算化学高有成效地处理的无机结构化学问题 本章介绍一些重要的量子理论的概念,以利于在以后对化学键理论的探讨。 1.1光和实物粒子的波粒二象性 上世纪初,科学家们已接受光既是一种粒子,也是一种波。光的波性特征显示在光的干涉 和衍射实验中。光的微粒性可在光电效应和Compton(康普顿)效应等实验中显现。根据这 些背景,L.de Broglie(德布罗意)在1924年提出假设:既然光是一种微粒又是一种波,实物粒 子也会有相似的二象性。他将A.Einstein(爱因斯坦)的质能联系公式(1.l,l)和M.Planck (普朗克)的量子化条件(1.1.2)式结合起来,得出光子的被长入和动量p的关系式(1.1.3): E=mc (1.1.1) E=hv (1.1.2) -部-点是-合 (1.1.3) 式中c是光速,h是Planck常数,v是辐射频率。De Broglie进一步假设具有静止质量为m,运 动速度为口的实物粒子也有相似的波长: A=久=么 my p (1.1.4) 仅限读者PB18030910本人使用、阅华请删除,不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播
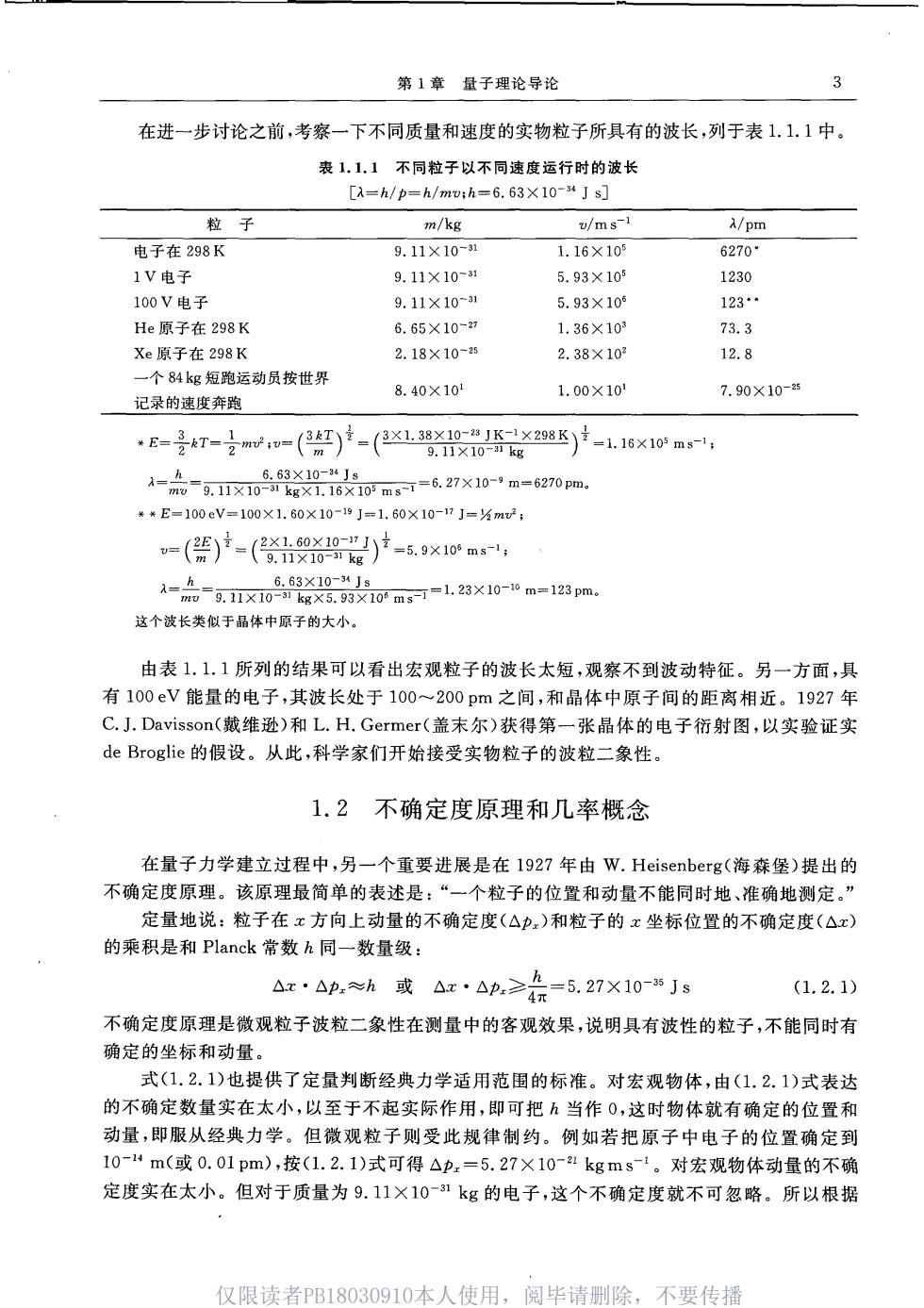
第1章量子理论导论 在进一步讨论之前,考察一下不同质量和速度的实物粒子所具有的波长,列于表1.1.1中。 表1,1,1不同粒子以不同速度运行时的波长 [a=h/p=h/mo:h=6.63X10-34Js] 粒子 m/kg u/ms-I A/pm 电子在298K 9.11×10-n 1.16×10 62701 1V电子 9.11×103 5.93×109 1230 100V由子 9.11×10-81 5.93×105 123 He原子在298K 6.65×10- 1.36×10 73.3 Xe原子在298K 2.18X10-4 2.38×10 12.8 一个84kg短跑运动员按世界 8.40×10 1.00×10 7.90×10-4 记录的速度奔跑 =-,=()-(21gx0X98K)-116x1oa, A=点=g.11X10561610m可=6.27×10-m=6270pm。 **E-100eV-100×1.60×10-”J=1.60×10-HJ-⅓mr2, =()产-(20019)-5.9×10ms-1 -品-1x028on=123X10-=123m 这个波长类似于品体中原子的大小。 由表1.11所列的结果可以看出宏观粒子的波长太短,观察不到波动特征。另一方面,具 有100eV能量的电子,其波长处于100~200pm之间,和晶体中原子间的距离相近。1927年 C.J.Davisson(戴维逊)和L.H.Germer(盖未尔)获得第一张晶体的电子衍射图,以实验证实 de Broglie的假设。从此,科学家们开始接受实物粒子的波粒二象性。 1.2不确定度原理和几率概念 在量子力学建立过程中,另一个重要进展是在l927年由W.Heisenberg(海森堡)提出的 不确定度原理。该原理最简单的表述是:“一个粒子的位置和动量不能同时地、准确地测定。” 定量地说:粒子在x方向上动量的不确定度(△p,)和粒子的x坐标位置的不确定度(△x) 的乘积是和Planck常数h同一数量级: △r·Ap.≈h或△x·△p,≥会=5.27X10Js (1.2.1) 不确定度原理是微观粒子波粒二象性在测量中的客观效果,说明具有波性的粒子,不能同时有 确定的坐标和动量。 式(1.2.1)也提供了定量判断经典力学适用范围的标准。对宏观物体,由(1.2.1)式表达 的不确定数量实在太小,以至于不起实际作用,即可把h当作0,这时物体就有确定的位置和 动量,即服从经典力学。但微观粒子则受此规律制约。例如若把原子中电子的位置确定到 10-“m(或0.01pm),按(1.2.1)式可得△p,=5.27×10~1kgms1。对宏观物体动量的不确 定度实在太小。但对于质量为9.11×10~kg的电子,这个不确定度就不可忽略。所以根据 仅限读者PB18030910本人使用, 阅毕请删除 不要传播
仅限读者PB18030910本人使用,阅毕请删除,不要传播