
第4章 Chapter 4 数据的概括性度量 ■ 一、学习指导 数据分布的特征可以从三个方面进行描述:一是分布的集中趋势,反映各数 据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心 值的趋势;三是分布的形状,反映数据分布偏斜程度和峰度。本章将从数据的不 同类型出发,分别介绍集中趋势测度值的计算方法、特点及其应用场合。本章各 节的主要内容和学习要点总结在下面的表格中。 章节 主要内容 学习要点 概念:众数。 众数 众数的特点 P用Excel中的统计函数计算众数。 中位数和分位数 的 4.1 集中趋势的 用Ex中的统计函数计算中位数 度 》概念:平均数,简单平均数,加权平均 数,几儿何平均数。 平均数 的统} 均数
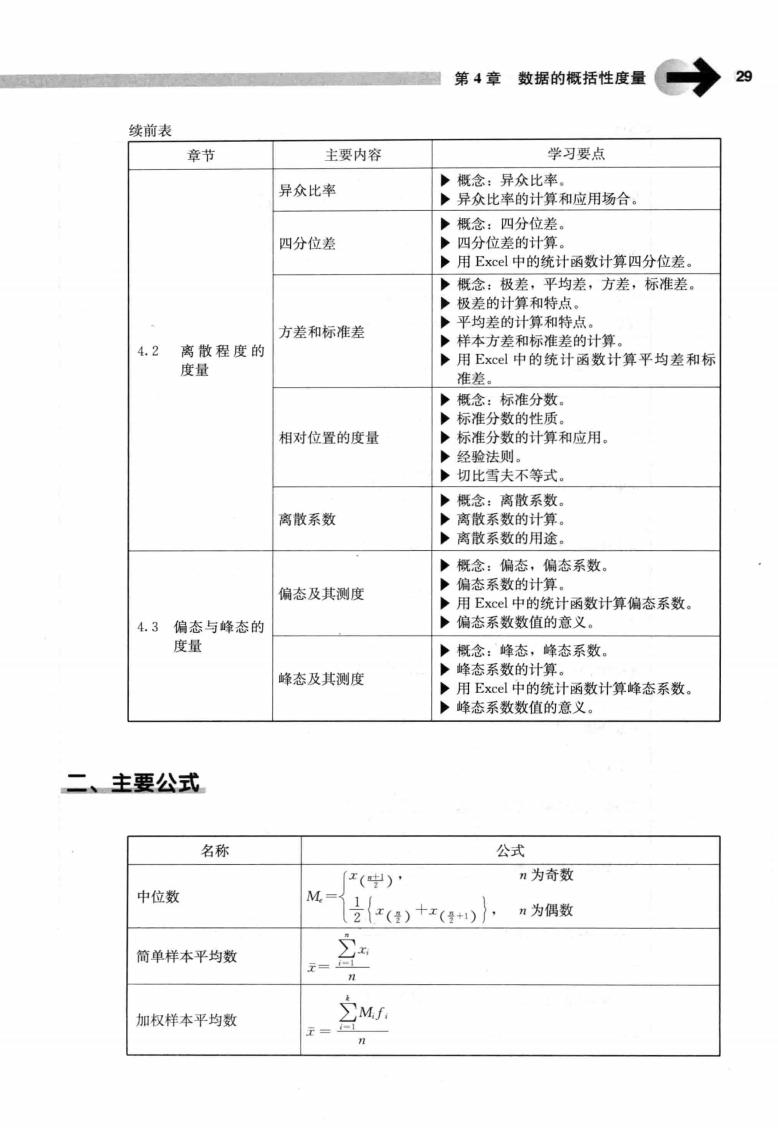
第4数的括性度量二 续前表 章节 主要内容 学习要点 异众比率 ●概念:四分位差。 四分位差 四分位差的计算。 用Excel中的统计函数计算四分位差。 算和特白 平均差的计算和特点 方差和标准差 样本方差和标准差的计算 4.2 离散程度的 度量 ,用Excl中的统计函数计算平均差和杨 的性质 相对位置的度量 标准分数的计算和应用。 经验法则 切比雪夫不等式。 概念:离散系数 离散系数 离散系数的计算 ●离散系数的用途 偏态及其测度 函数计算偏态系数。 4.3偏态与峰态的 度量 计 峰态及其测度 用Ex 中的 统计函数计算峰态系数 峰态系数数值的意义。 二、主要公式 名称 公式 (中) ”为奇数 中位数 M 受{:()十产()小n为偶数 简单样本平均数 加权样本平均数 之Mf

《统计学(第六版)》学习指导书 续前表 名称 公式 几何平均数 G=1Xm×…X无- 异众比率 ∑f 金 四分位差 Q-Q-Q 极差 R=max(,-min(x. 简单平均差 之玉- M,- 加权平均差 空1M-x万 M= 简单样本方差 2x- 一1 简单样本标准差 /2x- = -1 加权样本方差 M-p'f 2 -1 加权样本标准差 ∑M-xr =A ”-1 标准分数 6=, 离散系数 未分组数据的偏态系数 分组数据的偏态系数 2M-万 SK- 未分组数据的峰态系数 K= n(n+1D∑(x-x)-3∑(-x)](n-1D (m-1)(n-2)(m-3)5 分组数据的峰态系数 ∑M-'f K -3

第4章数据的概括性度量一 31 三、选择题 ①一组数据中出现频数最多的变量值称为()。 A众数 B.中位数 C.四分位数D.平均数 2下列关于众数的叙述,不正确的是()。 八.一组数据可能存在多个众数B.众数主要适用于分类数据 C.一组数据的众数是唯一的 D.众数不受极端值的影响 ③一组数据排序后处于中间位置上的变量值称为( A.众数 B.中位数 C.四分位数 D.平均数 4一组数据排序后处于25%和75%位置上的值称为( )。 A.众数 B.中位数 C.四分位数 D.平均数 ⑤非众数组的频数占总频数的比例称为( )。 A.异众比率 B.离散系数 C.平均差 D.标准差 6四分位差是( )。 A.上四分位数减下四分位数的结果 B.下四分位数减上四分位数的结果 C.下四分位数加上四分位数 D.下四分位数与上四分位数的中间值 ⑦一组数据的最大值与最小值之差称为( )。 A.平均差 B.标准差 C.极差 D.四分位差 8各变量值与其平均数离差平方的平均数称为( A.极差 B.平均差 C.方差 D.标准差 9变量值与其平均数的离差除以标准差后的值称为( A.标准分数 B.离散系数 C.方差 D.标准差 10如果一个数据的标准分数是一2,表明该数据( A.比平均数高出2个标准差 B.比平均数低2个标准差 C.等于2倍的平均数 D.等于2倍的标准差 1口如果一个数据的标准分数是3,表明该数据( A比平均数高出3个标准差 B.比平均数低3个标准差 C.等于3倍的平均数 D.等于3倍的标准差 12经验法则表明,当一组数据对称分布时,在平均数加减1个标准差的范 围之内大约有()

32 《统计学(第六版)》学习指导书■ A.68%的数据 B.95%的数据 C.99%的数据 D.100%的数据 3经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范 围之内大约有()。 A.68%的数据 B.95%的数据 C.99%的数据 D.100%的数据 4经验法则表明,当一组数据对称分布时,在平均数加减3个标准差的范 围之内大约有()。 A.68%的数据 B.95%的数据 C.99%的数据 D.100%的数据 5如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=2,其意 义是( A.至少有75%的数据落在平均数加减2个标准差的范围之内 B.至少有89%的数据落在平均数加减2个标准差的范围之内 C.至少有94%的数据落在平均数加减2个标准差的范围之内 D.至少有99%的数据落在平均数加减2个标准差的范围之内 46如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=3,其意 义是( A.至少有75%的数据落在平均数加减3个标准差的范围之内 B.至少有89%的数据落在平均数加减3个标准差的范围之内 C.至少有94%的数据落在平均数加减3个标准差的范围之内 D.至少有99%的数据落在平均数加减3个标准差的范围之内 口如果一组数据不是对称分布的,根据切比雪夫不等式,对于k一4,其意 义是()。 A.至少有75%的数据落在平均数加减4个标准差的范围之内 B.至少有89%的数据落在平均数加减4个标准差的范围之内 C.至少有94%的数据落在平均数加减4个标准差的范围之内 D.至少有99%的数据落在平均数加减4个标准差的范围之内 8离散系数的主要用途是()。 A.反映一组数据的离散程度 B.反映一组数据的平均水平 C.比较多组数据的离散程度 D.比较多组数据的平均水平 9比较两组数据的离散程度最适合的统计量是()。 A.极差 B.平均差 C.标准差 D.离散系数