
Load Flow Analysis 17 2.4.1 Rectangular Coordinates Method The power entering the bus i is given by S,=P+jQ =wr=v含vil2a ..(2.29) Where V=V:+jv, and Yik=Gik+jBik R+jo-k+2o-k.-长-jv (2.30) Expanding the right side of the above equation and separating out the real and imaginary parts. R=O-Bs+yGai-B》 .(2.31) Q,=2,Gk-Gs)-vGk+Gk》 ..(2.32) These are the two power relations at each bus and the linearized equations of the form (2.27)are written as △P OP OP P OP OVn-1 △Pnl P OPn-L OPn-1 OPn-1 av Ovn-1 OV aV n-1 .(2.33) 01 01 0Qn=L △Q1 8 Av, n-1 0 Qn-L Qn-1 04 △Qn-1 av △ n-1 Matrix equation(2.33)can be solved for the unknowns Av,and Av (i=1,2,...,n-1), leaving the slack bus at the nth bus where the voltage is specified.Equation(2.33)may be written compactly as N△v …(2.34)
Load Flow Analysis 2.4.1 Rectangular Coordinates Method The power entering the bus i is given by SI = PI + j QI Where and " =Vi I: =VILYI~ V,~,i=I,2, .... ,n v = VI + jVI I k=1 Ylk = Gik + j Bik (Pi + jQ) = ((v; + jv;·)t (Glk - jB'k Xv~ - v~)1 V~ - j y'~ k=1 'j 17 ..... (2.29) ..... (2.30) Expanding the right side of the above equation and separating out the real and imaginary parts. . .... (2.31 ) QI = t[v;(G lk v~ -Glk v~)-V;'(Glk v~ +Glk v~)] ..... (2.32) k=1 These are the two power relations at each bus and the linearized equations of the form (2.27) are written as ~P1 oP1 ~ OP1 ~ av'; av~_1 av~ av~-1 ~Pn-1 oPn-1 oPn-1 oPn-1 oPn-1 av'l av~_1 av~ av~_1 = 001 00"-1 001 00"-1 ~QI av'; av " av'; av " "-I "-I ..... (2.33) oon-I 00"-1 oon-I OOn-1 ~Qn-I av'l av av'; av " n-I 0-1 ~v 0-1 Matrix equation (2.33) can be solved for the unknowns~v; and ~v;' (i = 1,2'00" n -1), leaving the slack bus at the nth bus where the voltage is specified. Equation (2.33) may be written compactly as ..... (2.34)

18 Operation and Control in Power Systems where H,N,M and L are the sub-matrices of the Jacobian.The elements of the Jacobian are obtained by differentiating Egns.(2.31)and(2.32).The off-diagonal and diagonal elements of H matrix are given by 吧=GVk+BV,i≠k (2.35) -2GxV,-BaV,+B.v+Cavi-Bxvi) (2.36) aN k司 k士1 The off-diagonal and diagonal elements of N are 即=Gkk-BV,k≠i .(2.37) 四=-B,+20y+By+2Ga4+B) .(2.38) O k=l k The off-diagonal and diagonal elements of sub-matrix M are obtained as, =G,-Bkvi,k≠i .(2.39) N 0=Gy-0y-2B,-2Ge+B) …(2.40) k k Finally,the off-diagonal and diagonal elements of L are given by i--GxV;-BxVi,k+i N .(2.41) 0=G-2Bv-26-B) (2.42) O k=l It can be noticed that Lik =Hik and Nik=Mik This property of symmetry of the elements reduces computer time and storage
18 Operation and Control in Power Systems where H, N, M and L are the sub-matrices of the Jacobian. The elements of the Jacobian are obtained by differentiating Eqns. (2.31) and (2.32). The off-diagonal and diagonal elements of H matrix are given by oP· " -.-1 = G 1k V k + Blk V k ,i ~ k Ov k The off-diagonal and diagonal elements ofN are: oP· " . -.-1 =Gikv k -BikV ,k~i Ov k The off-diagonal and diagonal elements of sub-matrix M are obtained as, Finally, the off-diagonal and diagonal elements of L are given by It can be noticed that Lik =- Hik and Nik = Mik ..... (2.35) ..... (2.36) ..... (2.37) ..... (2.38) ..... (2.39) ..... (2.40) ..... (2.41 ) ..... (2.42) This property of symmetry of the elements reduces computer time and storage

Load Flow Analysis 19 Treatment of Generator Buses At all generator buses other than the swing bus,the voltage magnitudes are specified in addition to the real powers.At the ith generator bus V,2=v+v2 .(2.43) Then,at all the generator nodes,the variable AQ will have to be replaced by lv But, av.fav,ax ov, =2v,+△v,+2yAv ..(2.44) This is the only modification required to be introduced in eqn.(2.40) 2.4.2 The Polar Coordinates Method. The equation for the complex power at node i in the polar form is given in eqn.(2.10)and the real and reactive powers at bus i are indicated in eqn.(2.11)and(212).Reproducing them here once again for convenience. R-言V,V.Yos(6,-i-0) (2.11) and Q,=玄V,V,V in6,-8-0a) (2.12) The Jocobian is then formulated in terms ofV]and instead of Vand V in this case Egn.(2.27)then takes the form Lr& …(2.45) The off-diagonal and diagonal elements of the sub-matrices H,N,M and L are determined by differentiating eqns.(2.11)and(2.12)with respect to 8 and V]as before.The off-diagonal and diagonal elements of H matrix are 器-Wvs6-&-o:k …(2.46) 是-玄Xvem-&-) (2.47)
Load Flow Analysis 19 Treatment of Generator Buses At all generator buses other than the swing bus, the voltage magnitudes are specified in addition to the real powers. At the ith generator bus I 1 2 '2 "2 Vj =v, +v, ..... (2.43) Then, at all the generator nodes, the variable llQj will have to be replaced by lllVd 2 But, 1 1 2 _ a~ll,12) , a~t1,12) .. t1Vj - ,llV, + .. t1v. av, av, ..... (2.44) This is the only modification required to be introduced in eqn. (2.40) 2.4.2 The Polar Coordinates Method. The equation for the complex power at node i in the polar form is given in eqn. (2.10) and the real and reactive powers at bus i are indicated in eqn. (2.11) and (212). Reproducing them here once again for convenience. Pj = t lv, Vk Yjklcos(o, - Ok - ejk ) k=1 ..... (2.11) and n Q, = L IVj Vk Vjk Isin (OJ -Ok - e,k) ..... (2.12) k=1 The Jocobian is then formulated in terms of IV I and 0 instead of Vj' and Vj" in this case. Eqn. (2.27) then takes the form [:~l = [: ~l[ II ~~ Il ..... (2.45) The off-diagonal and diagonal elements of the sub-matrices H, N, M and L are determined by differentiating eqns. (2.11) and (2.12) with respect to 0 and IVI as before. The off-diagonal and diagonal elements of H matrix are OPj =IVj Vk V'klsin(o,-ok-e'k1j;~k aOk ..... (2.46) ..... (2.47)

20 Operation and Control in Power Systems The Jocobian is then formulated in terms of V]and 8 instead of V;and V,in this case. Eqn.(2.27)then takes the form AP1「HNA81 AQM LAIVI .(2.45) The off-diagonal and diagonal elements of the sub-matrices H,N,M and L are determined by differentiating eqns.(2.11)and(2.12)with respect to and V as before.The off-diagonal and diagonal elements of H matrix are V.vakin(6. (2.46) 震-含Ny6or .(2.47) 85 The off-diagonal and diagonal elements of N matrix are 识=,Yasin6,-i,-) alv (2.48) -2V.Y.ICos0+V YxlCos(6-8.-5) (2.49) alv,l k=1 The off-diagonal and diagonal elements of M matrix are 2Q-Hv.V:YalCos(6,-8.-0.) .(2.50) aδk 器-玄NVv6-8-8】 (2.51) Finally,the off-diagonal and diagonal elements of L matrix are 0=W,Ysin6,-δs-dk) alvkl (2.52) o0:2Y,Y.1cos0。+2N.Ysin6,-8-9k)2.-53) av, k=1 k1 It is seen from the elements of the Jacobian in this case that the symmetry that existed in the rectangular coordinates case is no longer present now.By selecting the variable as A8 and A VI/VI instead equation (2.45)will be in the form △δ N △V L .(2.54) In this case it will be seen that Hik=Lik
20 Operation and Control in Power Systems The Jocobian is [hen formulated in terms of IV I and 8 instead of V,' and V," in this case. Eqn. (2.27) then takes the form [~]=[: :][~~~I] ..... (2.45) The off-diagonal and diagonal elements of the sub-matrices H, N, M and L are determined by differentiating eqns. (2.11) and (2.12) with respect to 8 and IVI as before. The off-diagonal and diagonal elements of H matrix are oP, = lV, Vk Y'klsin(8, -8k -e'k~i;t:k o8k aP n -' = I lv, Vk Y,kI COS(D, -Dk -8,k1i;t: k aD. K=I The off-diagonal and diagonal elements ofN matrix are ~=IV Yklsin(o -Ok -8 k) al Vk i '" , ap n --'- = 21 Vi YII ICose'i + L IV. V,. ICos(8, - 8k - O,k) al V, I k=1 k;t' The off-diagonal and diagonal elements ofM matrix are aQ, = -Iv, Vk Y,k ICos (0, - Ok - e,k) aO k aQ n -' = L IV; Vk V'kICOS(O, -Ok -e,.) aO, k=1 Finally, the off-diagonal and diagonal elements of L matrix are ..... (2.46) ..... (2.47) ..... (2.48) ..... (2.49) ..... (2.50) ..... (2.51 ) oQ, = lV, Y.k Isin (8 - 8k - e'k) (252) 01 Vk I " " ..... . ~ =12V, Yi , ICOSe'i + f IVk Yik ISin (8, - Ok - e,k) ..... (2.53) o I V, I k=1 It is seen from the elements of the Jacobian in this case that the symmetry that existed in the rectangular coordinates case is no longer present now. By selecting the variable as ~8 and ~ IVI / IVI instead equation (2.45) will be in the form ~Q ~P] = [H M L N] [~~'l IVI In this case it will be seen that Hik = L,k ..... (2.54 )
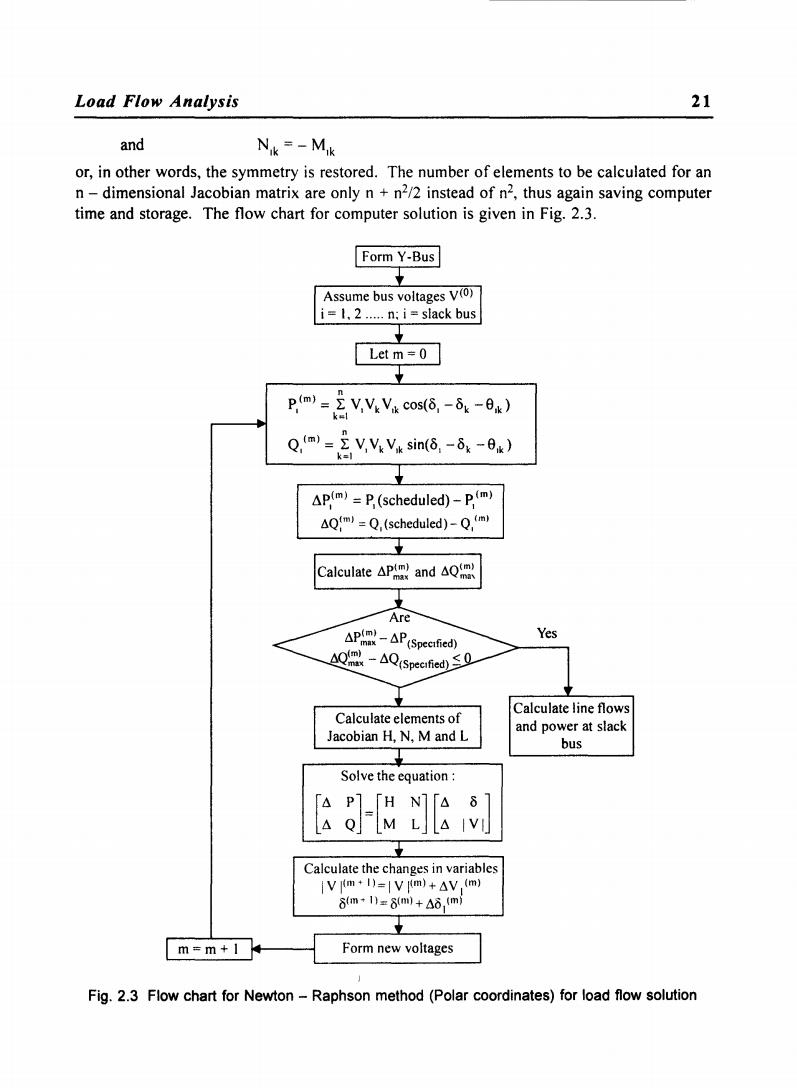
Load Flow Analysis 21 and Nik=-Mik or,in other words,the symmetry is restored.The number of elements to be calculated for an n-dimensional Jacobian matrix are only n +n2/2 instead of n2,thus again saving computer time and storage.The flow chart for computer solution is given in Fig.2.3. Form Y-Bus Assume bus voltages V(0) i=1.2.....n:i=slack bus Let m=0 p.m)=ΣV,VV cos(6,-δk-6k) Q.m)-V.V.Va sin(6,-5:-0x) k=l AP(m)=P(scheduled)-p(m) )=Q,(scheduled)-Q(m) Calculate△Pm,and Q Are APP(Specrfied) Yes △Q-A(Specfed)0 立 Calculate line flows Calculate elements of and power at slack Jacobian H,N,M and L bus Solve the equation P「HN]fa 8 Calculate the changes in variables iVm+I)=1Vm)+△,(m) 8m*1=8m)+Aδ,m m=m+1 Form new voltages Fig.2.3 Flow chart for Newton-Raphson method(Polar coordinates)for load flow solution
Load Flow Analysis 21 and N,k = - M,k or, in other words, the symmetry is restored. The number of elements to be calculated for an n-dimensional Jacobian matrix are only n + n2/2 instead of n2, thus again saving computer time and storage. The flow chart for computer solution is given in Fig. 2.3. m=m+ I ~p(m) = P (scheduled) _ P (m) " , l\Q:m) '" Q, (scheduled) _ Q,(m) Solve the equation: [~ ~]=[: ~] [~ I~I] Calculate the changes in variables I V 1(111 + 1)= I V 1(111) + 6 V 1(111) 8(111+ 1)=8(111)+68 1 (111) Yes Calculate line flows and power at slack bus Fig. 2.3 Flow chart for Newton - Raphson method (Polar coordinates) for load flow solution