广东工业大学：《土力学》课程电子教案（负责人：刘勇健）

广东工业大学2019-2020学年第一学期 《土力学》教案 序号第6次 授课学时 2学时 授课班级 土木17(1,2)班 周次第4周 日期 2019.9.19 节次 第34节 第3章土中应力 31概述 (章节)题目 32土中自重应力 33基底压力 1.了解土中的应力形式 教学目的 2.掌握自重应力的计算方法 3掌握基底压力概念和计算方法 教学重点 成层土和有地下水时自重应力计算、偏心荷载下的基底压力计算 教学难点 成层土和有地下水时自重应力计算、偏心荷载下的基底压力计算 教学方法 案例式、启发式、线上线下融合 课程思政目标 工程伦理、工匠精神 与融入点 信息技术 铺助手段 “土力学”新云谋堂https://courses.gdut..edu.cn/course/view.php2d:21 第3音地基中的应力计算 土中应力类型 3.2土中的自重应力计算中的应力状态 3.3,1均质士自重应力 自重应力 土体初始应力，指由土体自身的有效重力产生的应力。 假定上体具有水平表面的半无限弹性体 士体中所有竖直面和水平面均不存在剪应力 教学内容 及教学过程 w☑ 对于天然重度为y的均质士 0e= 式中 第层土的重度，kNm,地下水位以上的士层一般采用天然重度，地 下水位以下的士层采用浮重度，毛细饱和带的士层采用饱和重度 水平向自重应力 根据弹性力学广义虎克定律和土体的侧限条件，推导得 a=a=Kg 式中 K -土的侧压力系数（也称静止土压力系数）

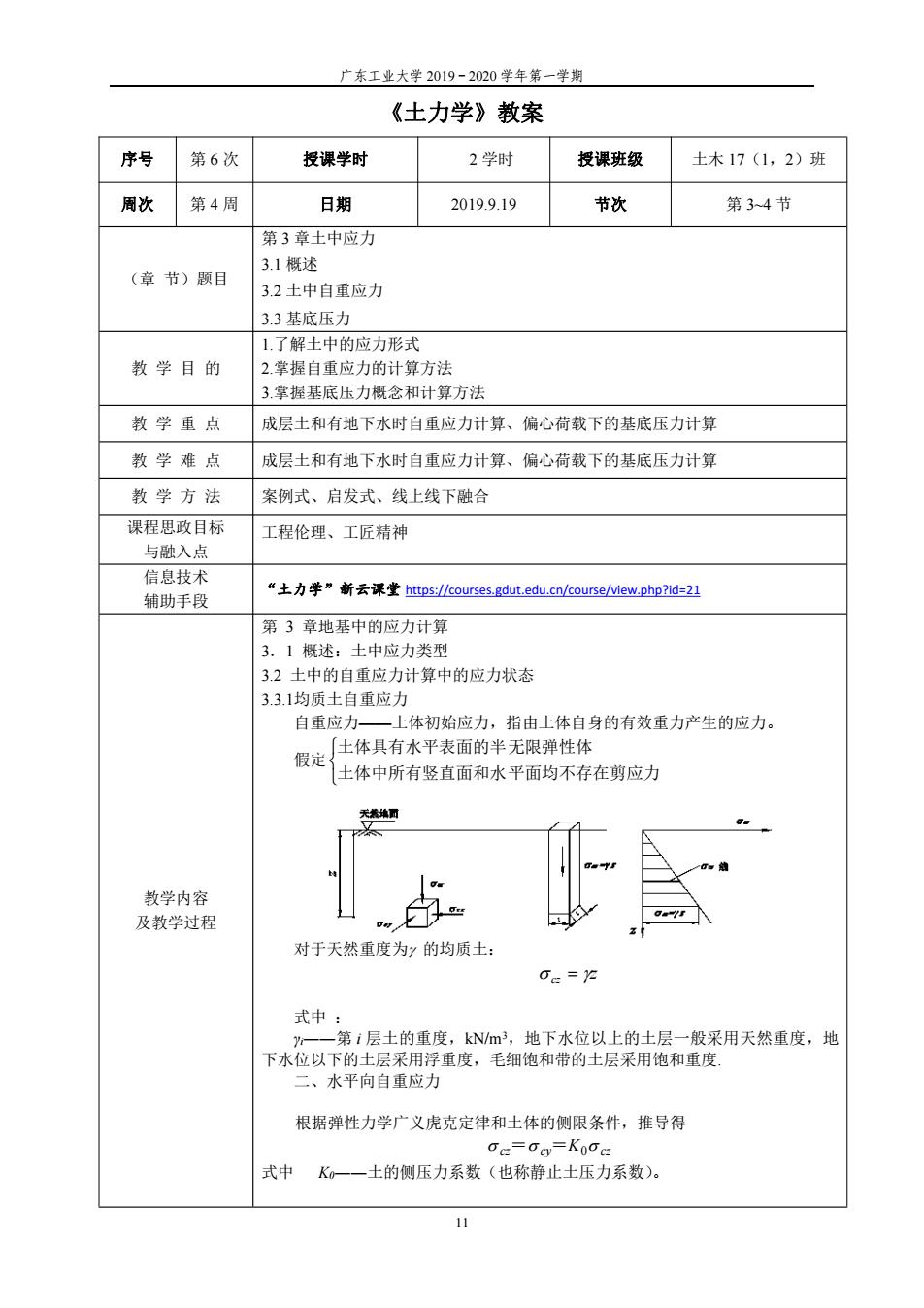
广东工业大学 2019－2020 学年第一学期 11 《土力学》教案 序号 第 6 次 授课学时 2 学时 授课班级 土木 17（1，2）班 周次 第 4 周 日期 2019.9.19 节次 第 3~4 节 （章 节）题目 第 3 章土中应力 3.1 概述 3.2 土中自重应力 3.3 基底压力 教 学 目 的 1.了解土中的应力形式 2.掌握自重应力的计算方法 3.掌握基底压力概念和计算方法 教 学 重 点 成层土和有地下水时自重应力计算、偏心荷载下的基底压力计算 教 学 难 点 成层土和有地下水时自重应力计算、偏心荷载下的基底压力计算 教 学 方 法 案例式、启发式、线上线下融合 课程思政目标 与融入点 工程伦理、工匠精神 信息技术 辅助手段 “土力学”新云课堂 https://courses.gdut.edu.cn/course/view.php?id=21 教学内容 及教学过程 第 3 章地基中的应力计算 3．1 概述：土中应力类型 3.2 土中的自重应力计算中的应力状态 3.3.1均质土自重应力 自重应力——土体初始应力，指由土体自身的有效重力产生的应力。 假定    土体中所有竖直面和水平面均不存在剪应力 土体具有水平表面的半无限弹性体 对于天然重度为 的均质土： z cz    式中 ： γi――第 i 层土的重度，kN/m3，地下水位以上的土层一般采用天然重度，地 下水位以下的土层采用浮重度，毛细饱和带的土层采用饱和重度. 二、水平向自重应力 根据弹性力学广义虎克定律和土体的侧限条件，推导得  cz＝ cy＝K0 cz 式中 K0――土的侧压力系数（也称静止土压力系数）

广东工业大学2019-2020学年第一学期 3.22层成士自重应力 对于成层土，并存在地下水： o。=h+h++h=2h 注意： 计算， ②新近沉积的土层或新近堆填的土层，在自重应力作用下的变形尚未完成， 还应考虑它们在自重应力作用下的变形。 3.2.3水位升降时自重应力 【课堂讨论】地下水位的升降是否会引起土中自重应力的变化？ 地下水位的升降会引起土中自重应力的变化，例如，大量抽取地下水造 成地下水位大幅度下降，使原水位以下土体中的有效应力增加，造成地表大面积 下沉。 3.3基底压力计算 331基底压力分布规律 3.3.2基底压力及其简化计算 一、中心荷载作用下的基底压力 基底压力 建筑物上部结构荷载和基础自重通过基础传递给地基，作用于 基础底面传至地基的单位面积压力，又称接触压力。 基底反力一基底压力的反作用力即地基土层反向施加于基础底面上的压 力。 「基础 影响基底压力的分布和大小的因素{荷载 地基土性质 基底压力的简化计算： 当基础宽度不太大， 而荷载较小的情况下，基底压力分布近似按直线变化考 虑，根据材料力学公式进行简化计算，即 F+G P=- ,kPa。 A 对于荷载沿长度方向均匀分布的条形基础，则沿长度方向截取1m的基底面积 来计算，单位为kNm 二、偏心荷载作用下的基底压力 刳 讨论： 当e<。时，基底压力呈梯形分布： 当e=二时，基底压力呈三角形分布： 12

广东工业大学 2019－2020 学年第一学期 12 3.2 .2层成土自重应力 对于成层土，并存在地下水： i n i cz h h nhn  ih        1 1 1 2 2      注意： ①在地下水位以下，若埋藏有不透水层（如基岩层、连续分布的硬粘性土层）， 不透水层中不存在水的浮力，层面及层面以下的自重应力按上覆土层的水土总重 计算； ②新近沉积的土层或新近堆填的土层，在自重应力作用下的变形尚未完成， 还应考虑它们在自重应力作用下的变形。 3.2.3水位升降时自重应力 【课堂讨论】地下水位的升降是否会引起土中自重应力的变化？ ——地下水位的升降会引起土中自重应力的变化，例如，大量抽取地下水造 成地下水位大幅度下降，使原水位以下土体中的有效应力增加，造成地表大面积 下沉。 3.3 基底压力计算 3.3.1 基底压力分布规律 3.3.2 基底压力及其简化计算 一、中心荷载作用下的基底压力 基底压力——建筑物上部结构荷载和基础自重通过基础传递给地基，作用于 基础底面传至地基的单位面积压力，又称接触压力。 基底反力——基底压力的反作用力即地基土层反向施加于基础底面上的压 力。 影响基底压力的分布和大小的因素      地基土性质 荷载 基础 基底压力的简化计算： 当基础宽度不太大，而荷载较小的情况下，基底压力分布近似按直线变化考 虑，根据材料力学公式进行简化计算，即 A F G p  ＝ ，kPa 。 对于荷载沿长度方向均匀分布的条形基础，则沿长度方向截取 1m 的基底面积 来计算，单位为 kN/m。 二、偏心荷载作用下的基底压力          l e bl F G p p 6 1 min max 讨论： 当 6 l e  时，基底压力呈梯形分布； 当 6 l e  时，基底压力呈三角形分布；

广东工业大学2019-2020学年第一学期 当e>时，基底压力Pmm<0,表明基底出现拉应力，此时，基底与地基间 局部脱离，而使基底压力重新分布。 注意：当计算得到P 时， 般应调整结构设计和基础尺寸设计，以避匀 基底与地基间局部脱离的情况。 对作用于建筑物上的水平荷载，计算基底压力时，通常按均匀分布于整个基 础底面计算。 433基底附加压力计算 基底附加压力 作用于地基表面，由于建造建筑物而新增加的压力，即与 致地基中产生附加应力的那部分基底压力。 基底附加压力在数值上等于基底压力扣除基底标高处原有土体的自重应力。 即 基底压力均匀分布时： Po=P-Yod 基底压力呈梯形分布时，基底附加压力为： 月久。-d 式中P。一一基底附加压力设计值，kPa: P一一基底压力设计值，kPa: LF+0 T或 己 基底附加压力图 基底标高以上各天然土层的加权平均重度，kNWm3:地下水位以下取 有效重度 d一一从天然地面起算的基础埋深，m。 【课堂讨论】求基底附加应力意义何在？ 【木持课小结】 【非均质士中自重应力沿深度星折线分布 思考题 2。自重应力分布在重度变化的士层界面和地下水位面上发生转折 作业 3.自重应力分布在不透水层面处发生突变： 4.地下水位下降会引起自重应力增加。 5.中心、偏心荷载作用下的基底压力计算。 课后作业3题

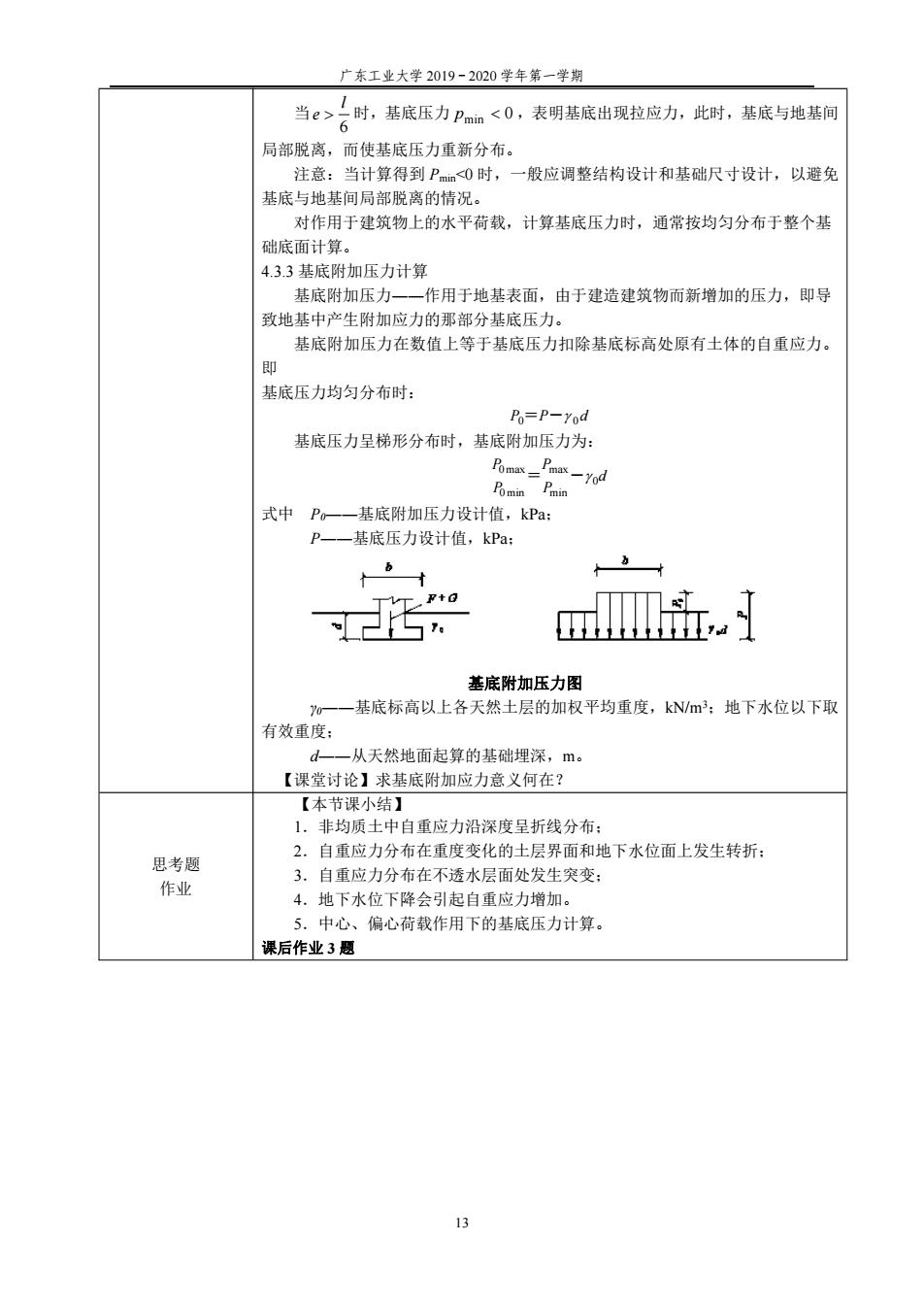
广东工业大学 2019－2020 学年第一学期 13 当 6 l e  时，基底压力 m 0 p in  ，表明基底出现拉应力，此时，基底与地基间 局部脱离，而使基底压力重新分布。 注意：当计算得到 Pmin<0 时，一般应调整结构设计和基础尺寸设计，以避免 基底与地基间局部脱离的情况。 对作用于建筑物上的水平荷载，计算基底压力时，通常按均匀分布于整个基 础底面计算。 4.3.3 基底附加压力计算 基底附加压力――作用于地基表面，由于建造建筑物而新增加的压力，即导 致地基中产生附加应力的那部分基底压力。 基底附加压力在数值上等于基底压力扣除基底标高处原有土体的自重应力。 即 基底压力均匀分布时： P0＝P－ 0 d 基底压力呈梯形分布时，基底附加压力为： d P P P P 0 min max 0min 0max＝ － 式中 P0――基底附加压力设计值，kPa； P――基底压力设计值，kPa； 基底附加压力图 γ0――基底标高以上各天然土层的加权平均重度，kN/m3；地下水位以下取 有效重度； d――从天然地面起算的基础埋深，m。 【课堂讨论】求基底附加应力意义何在？ 思考题 作业 【本节课小结】 1．非均质土中自重应力沿深度呈折线分布； 2．自重应力分布在重度变化的土层界面和地下水位面上发生转折； 3．自重应力分布在不透水层面处发生突变； 4．地下水位下降会引起自重应力增加。 5．中心、偏心荷载作用下的基底压力计算。 课后作业 3 题

广东工业大学2019-2020学年第一学期 《土力学》教案 序号第7次 授课学时 2学时 授课班级 土木17(1,2)班 周次 第4周 日期 2019.9.25 节次 第34节 (章节)题目 3.3地基附加应力 3.4有效应力原理 教学目的 让学生掌握各种分布荷载作用下附加应力计算方法及应用 1.了解弹性半空间布辛内斯克课题理论 教学重点 2.掌握士中矩形基础均布荷载的附加应力计算方法。 3.掌握附加应力叠加方法和分部角点计算方法。 教学难点 土中附加应力计算及分布规律 教学方法 案例式、启发式、线上线下融合 课程思政目标 工程伦理、工匠精神 与融入点 信息技术辅助手段“土力学”新云课堂https://courses.gdut..edu.cn/course/view.phpid2L 第3章地基中的应力计算 3.3地基土中的附加应力计算 附加应力一一新增外加荷载在地基土体中引起的应力。 假定一一地基土是连续、均匀、各项同性的半无限完全弹性体。 空间问题一 一附加应力是三维坐标人、2的函数： 平面问题 一附加应力是二维坐标不、2的函数 器前 1 一、竖向集中荷载作用下的地基附加应力 教学内容 布辛涅斯克用弹性理论推导得出 及教学过程 依上述公式可推导出附加应力，的分布规律： (1)地面下任一深度的水平面上，在集中力作用线上的附加应力最大，向两侧逐渐 成小. (②)同一竖向线上的附加应力随深度而变化，在集中力作用线上，当z=0时，·， ,®，随着深度增加， ,逐渐减小 )面图上的附加应力等值线，在空间上附加应力等值面呈泡状，称应力泡。 应力扩散一一竖向集中力作用引起的附加应力向深部向四周无限传播，在传播 过程中，应力强度不断降低，这种现象称为应力扩散。 【课堂讨论】相邻基础会不会相互影响？ 二、矩形基础地基中的附加应力计算 矩形基础长度为1，基础宽度为，当/K10,其地基附加应力计算问题属于空间 问题

广东工业大学 2019－2020 学年第一学期 14 《土力学》教案 序号 第 7 次 授课学时 2 学时 授课班级 土木 17（1，2）班 周次 第 4 周 日期 2019.9.25 节次 第 3~4 节 （章 节）题目 3.3 地基附加应力 3.4 有效应力原理 教 学 目 的 让学生掌握各种分布荷载作用下附加应力计算方法及应用 教 学 重 点 1.了解弹性半空间布辛内斯克课题理论 2.掌握土中矩形基础均布荷载的附加应力计算方法。 3.掌握附加应力叠加方法和分部角点计算方法。 教 学 难 点 土中附加应力计算及分布规律 教 学 方 法 案例式、启发式、线上线下融合 课程思政目标 与融入点 工程伦理、工匠精神 信息技术辅助手段 “土力学”新云课堂 https://courses.gdut.edu.cn/course/view.php?id=21 教学内容 及教学过程 第 3 章 地基中的应力计算 3.3 地基土中的附加应力计算 附加应力――新增外加荷载在地基土体中引起的应力。 假定——地基土是连续、均匀、各项同性的半无限完全弹性体。 空间问题——附加应力是三维坐标 x、y、z 的函数； 平面问题——附加应力是二维坐标 x、z 的函数。 一、竖向集中荷载作用下的地基附加应力 布辛涅斯克用弹性理论推导得出： 依上述公式可推导出附加应力σz的分布规律： (1)地面下任一深度的水平面上，在集中力作用线上的附加应力最大，向两侧逐渐 减小； (2)同一竖向线上的附加应力随深度而变化，在集中力作用线上，当 z＝0 时，σz →∞，随着深度增加，σz逐渐减小； (3)剖面图上的附加应力等值线，在空间上附加应力等值面呈泡状，称应力泡。 应力扩散――竖向集中力作用引起的附加应力向深部向四周无限传播，在传播 过程中，应力强度不断降低，这种现象称为应力扩散。 【课堂讨论】相邻基础会不会相互影响？ 二、矩形基础地基中的附加应力计算 矩形基础长度为 l，基础宽度为 b，当 l/b<10,其地基附加应力计算问题属于空间 问题

广东工业大学2019-2020学年第一学期 1.竖向均布荷载P作用于矩形基底 依布辛涅斯克解，将公式沿长度1和宽度b两个方向二重积分，求得角点下任一深 度z处M点的附加应力： g品e 3 简写成g:=KP 式中《一一垂直均布荷载下矩形基底角点下的竖向附加应力系数，无量纲，= (a,,可由表查得 注意：1为基础长边，b为基础短边：z是从基底面起算的深度：P为基底附加压力， 2.“角点法 角点法之实质一一附加应力叠加原理。角点其实是附加应力积分公式的原点，因而 不在角点（原点）下的附加应力不能直接求出。 (e) 角点法的应用： (1)矩形荷载面内任一点0之下的附加应力[如图(a)所示]： =(Ke l+Kel +Keml +Kcv )P (2)矩形荷载面边缘上任一点0之下的附加应力[如图(b)所示]： (3)矩形荷载面边缘外 一点0之下的附加应力[如图(c)所示]： G:=(Ker-Ken+Kem-KeN)p 其中I为ofbg,Ⅲ为oecg 注意：基础范围外“虚线”所构成的矩形其实是虚设的荷载分布的范围，因而要减 去其“产生”的附加应力 (4)矩形荷载面外任一点0之下的附加应[如图(所示]： a:=K。rkn-Kem+kwP 其中I为ohce,Ⅱ为ogde,Ⅲ为ohbf。 【课堂讨论】作“辅助线”原理及目的何在？ 3.垂直三角形分布荷载 G:=Knp K一-可由表查得，其中Fl/b,Fz/b。 同理，荷载强度最大值角点2下任一深度z处M点的附加应力为 =Kep 注意：b为沿荷载变化方向矩形基底边长，1为矩形基底另一边长：同理，计算中 可利用角点法。 四、均布圆形荷载下的地基附加应力

广东工业大学 2019－2020 学年第一学期 15 1．竖向均布荷载 P 作用于矩形基底 依布辛涅斯克解，将公式沿长度 l 和宽度 b 两个方向二重积分，求得角点下任一深 度 z 处 M 点的附加应力：   dxdy x y z l b p z z 5/ 2 2 2 2 3 0 0 2 3        简写成  z  Kc P 式中 Kc――垂直均布荷载下矩形基底角点下的竖向附加应力系数，无量纲，Kc=f (m ,n)，可由表查得。 注意：l 为基础长边，b 为基础短边；z 是从基底面起算的深度；P 为基底附加压力。 2．“角点法” 角点法之实质——附加应力叠加原理。角点其实是附加应力积分公式的原点，因而 不在角点（原点）下的附加应力不能直接求出。 (a) (b) (c) (d) 角点法的应用： （1）矩形荷载面内任一点 O 之下的附加应力[如图（a）所示]：  z  KcⅠKcⅡ  KcⅢ KcⅣP （2）矩形荷载面边缘上任一点 O 之下的附加应力[如图（b）所示]：  z  KcⅠKcⅡP （3）矩形荷载面边缘外一点 O 之下的附加应力[如图（c）所示]：  z  KcⅠKcⅡ  KcⅢ KcⅣP 其中Ⅰ为 ofbg，Ⅲ为 oecg。 注意：基础范围外“虚线”所构成的矩形其实是虚设的荷载分布的范围，因而要减 去其“产生”的附加应力； （4）矩形荷载面外任一点 O 之下的附加应力[如图（d）所示]：  z  KcⅠKcⅡ  KcⅢ KcⅣP 其中Ⅰ为 ohce，Ⅱ为 ogde，Ⅲ为 ohbf。 【课堂讨论】作“辅助线”原理及目的何在？ 3．垂直三角形分布荷载  z  Kt1 pt Kt1――可由表查得，其中 m=l/b，n=z/b。 同理，荷载强度最大值角点 2 下任一深度 z 处 M 点的附加应力为 z t t K p   2 注意： b 为沿荷载变化方向矩形基底边长，l 为矩形基底另一边长；同理，计算中 可利用角点法。 四、均布圆形荷载下的地基附加应力