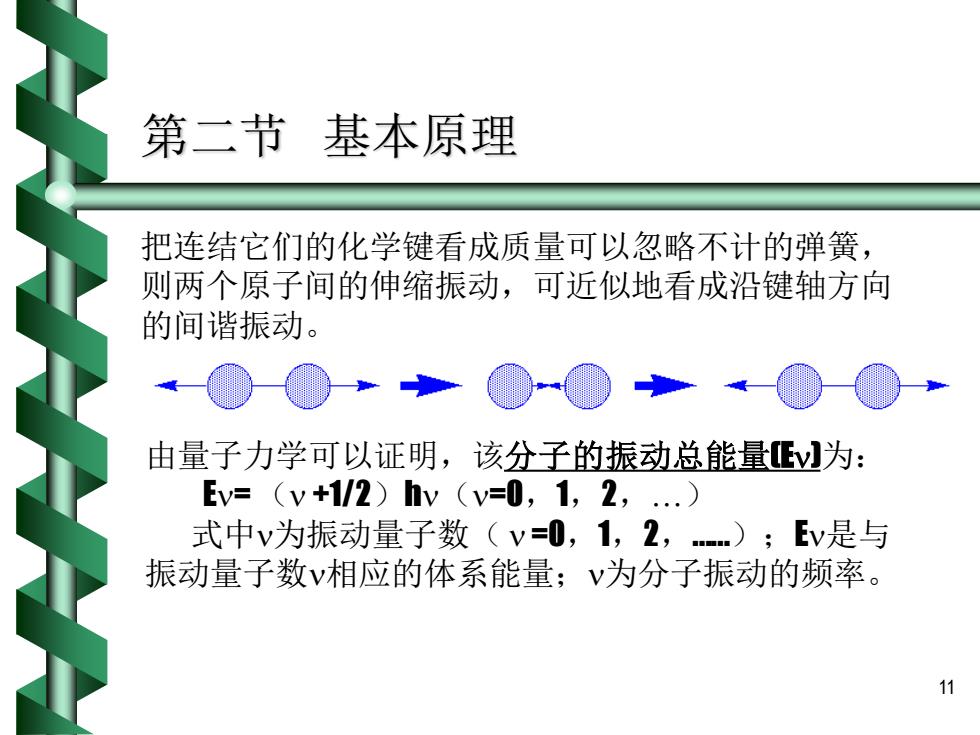
第二节基本原理 把连结它们的化学键看成质量可以忽略不计的弹簧, 则两个原子间的伸缩振动,可近似地看成沿键轴方向 的间谐振动。 由量子力学可以证明,该分子的振动总能量为: Ev=(v+1/2)hv(v=0,1,2,.) 式中v为振动量子数(v=0,1,2,);Ev是与 振动量子数v相应的体系能量;v为分子振动的频率。 11
11 第二节 基本原理 把连结它们的化学键看成质量可以忽略不计的弹簧, 则两个原子间的伸缩振动,可近似地看成沿键轴方向 的间谐振动。 由量子力学可以证明,该分子的振动总能量(E)为: E= ( +1/2)h(=0,1,2,) 式中为振动量子数( =0,1,2,.);E是与 振动量子数相应的体系能量;为分子振动的频率

第二节基本原理 在室温时,分子处于基态(v=0),E=l/2hv,此 时,伸缩振动的频率很小。 当有红外辐射照射到分子时, 若红外辐射的光子(V)所具有的能量(E)恰好等于 分子振动能级的能量差(△E振)时,则分子将吸收红外 辐射而跃迁至激发态,导致振幅增大。分子振动能级的 能量差为 △E振=△vhv 又光子能量为 EL=hvL 于是可得产生红外吸收光谱的第一条件为: E=△E振 即v=△vv 12
12 第二节 基本原理 在室温时,分子处于基态(=0),E = 1/2•h,此 时,伸缩振动的频率很小。当有红外辐射照射到分子时, 若红外辐射的光子(L)所具有的能量(EL)恰好等于 分子振动能级的能量差(△E振)时,则分子将吸收红外 辐射而跃迁至激发态,导致振幅增大。分子振动能级的 能量差为 △E振=△•h 又光子能量为 EL=hL 于是可得产生红外吸收光谱的第一条件为: EL =△E振 即L =△•

第二节基本原理 '.只有当红外辐射频率等于振动量子数的差值与分子 振动频率的乘积时,分子才能吸收红外辐射,产生红外 吸收光谱。 基频峰:分子吸收红外辐射后,由基态振动能级(=0) 跃迁至第一振动激发态(ν=1)时,所产生的吸收峰。因 为△v=1时,V=v,所以基频峰的位置(v)等于分子的 振动频率。 倍频峰:在红外吸收光谱上除基频峰外,还有振动能级 由基态(v=O)跃迁至第二激发态(v=2)、第三激发态 (V=3).,所产生的吸收峰。 13
13 第二节 基本原理 ∴只有当红外辐射频率等于振动量子数的差值与分子 振动频率的乘积时,分子才能吸收红外辐射,产生红外 吸收光谱。 基频峰:分子吸收红外辐射后,由基态振动能级(=0) 跃迁至第一振动激发态(=1)时,所产生的吸收峰。因 为△=1时,L =,所以 基频峰的位置(L)等于分子的 振动频率。 倍频峰:在红外吸收光谱上除基频峰外,还有振动能级 由基态( =0)跃迁至第二激发态( =2)、第三激发态 ( =3),所产生的吸收峰

第二节基本原理 倍频峰:由v=0跃迁至v=2时,△v=2,则y,=2v,即吸 百尔线谱线()是分子振动频率的倍, 吸收峰。 三倍频峰:由v=0跃迁至v=3时,△v=3,则y=3v,即吸 收的红外线谱线(ν)是分子振动频率的三倍,产生 的吸收峰。 其它类推,在倍频峰中,二倍频峰还比较强。三倍频 峰以上,因跃迁几率很小,一般都很弱,常常不能测到。 由于分子非谐振性质,各倍频峰并非正好是基频峰 的整数倍,而是略小一些。 以HCI为例: 14
14 第二节 基本原理 二倍频峰:由=0跃迁至=2时,△=2,则L=2,即吸 收的红外线谱线( L )是分子振动频率的二倍,产生的 吸收峰。 三倍频峰:由=0跃迁至=3时,△=3,则L=3,即吸 收的红外线 谱线( L )是分子振动频率的三倍,产生 的吸收峰。 其它类推,在倍频峰中,二倍频峰还比较强。三倍频 峰以上,因跃迁几率很小,一般都很弱,常常不能测到。 由于分子非谐振性质,各倍频峰并非正好是基频峰 的整数倍,而是略小一些。以HCl为例:

第二节基本原理 基频峰(Vo1) 2885.9cm-1 最强 二倍频峰(Vo→2) 5668.0cm1 较弱 三倍频峰 (Vo-3) 8346.9cm-1 很弱 四倍频峰 (V0-4) 10923.1cm-1 极弱 五倍频峰(Vo-5) 13396.5cm-1 极弱 除此之外,还有合频峰 (V1+V2,2V1+V2, .),差频峰(V1-V2,2V1-V2,.) 等,这些峰 多数很弱,一般不容易辨认。倍频峰、合频峰和 差频峰统称为泛频峰 15
15 第二节 基本原理 基频峰(0→1) 2885.9 cm-1 最强 二倍频峰( 0→2 ) 5668.0 cm-1 较弱 三倍频峰( 0→3 ) 8346.9 cm-1 很弱 四倍频峰( 0→4 ) 10923.1 cm-1 极弱 五倍频峰( 0→5 ) 13396.5 cm-1 极弱 除此之外,还有合频峰(1+2,21+2, ),差频峰( 1 -2,21 -2, )等,这些峰 多数很弱,一般不容易辨认。倍频峰、合频峰和 差频峰统称为泛频峰