9-2电容电容器 第九章静电场中的导体和电介质 孤立导体的电容 单位 IF=1C/V 1uF=106F 1pF=10-12F 例如孤立的导体球的电容 4nt EoR 4饥EoR 地球 Rε=6.4×10m,CE≈7×104F
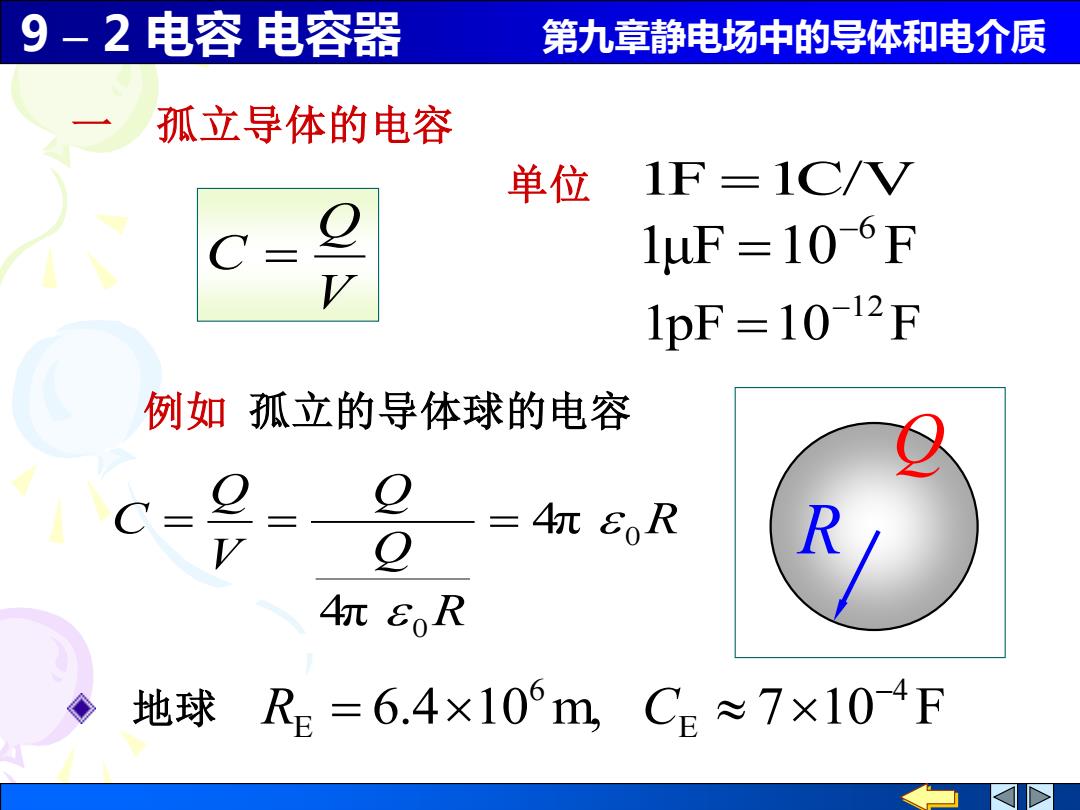
9 – 2 电容 电容器 第九章静电场中的导体和电介质 一 孤立导体的电容 V Q C = 例如 孤立的导体球的电容 R R Q Q V Q C 0 0 4π 4π = = = R Q 6.4 10 m, 7 10 F 4 E 6 E − 地球 R = C 单位 1F =1C/V 1pF 10 F −12 = 1μF 10 F −6 =
9-2电容电容器 第九章静电场中的导体和电介质 二 电容器 电容器电容 Va-VR 电容的大小仅与导体的形状、相对位置、其间的 电介质有关.与所带电荷量无关 三 电容器电容的计算 步骤 1)设两极板分别带电±Q;2)求E; 3)求U;4)求C
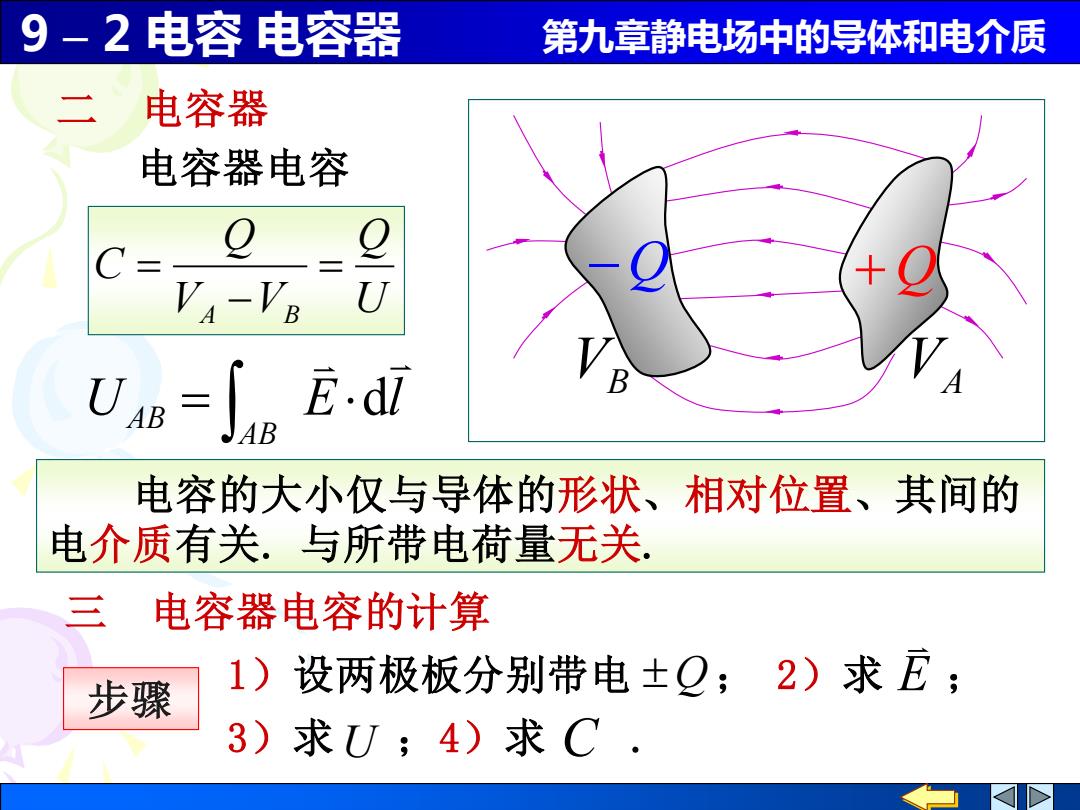
9 – 2 电容 电容器 第九章静电场中的导体和电介质 二 电容器 电容器电容 U Q V V Q C A B = − = 电容的大小仅与导体的形状、相对位置、其间的 电介质有关. 与所带电荷量无关. 三 电容器电容的计算 VB VA −Q + Q 1)设两极板分别带电 Q ; 2)求 E ; 3)求 U ;4)求 C . 步骤 U E l AB AB = d
9-2电容电容器 第九章静电场中的导体和电介质 1平板电容器 (1)设两导体板分别带电±Q (2)两带电平板间的电场强度 E= S Eo EoS (3)两带电平板间的电势差 U=Ed= Od EoS (4)平板电容器电容
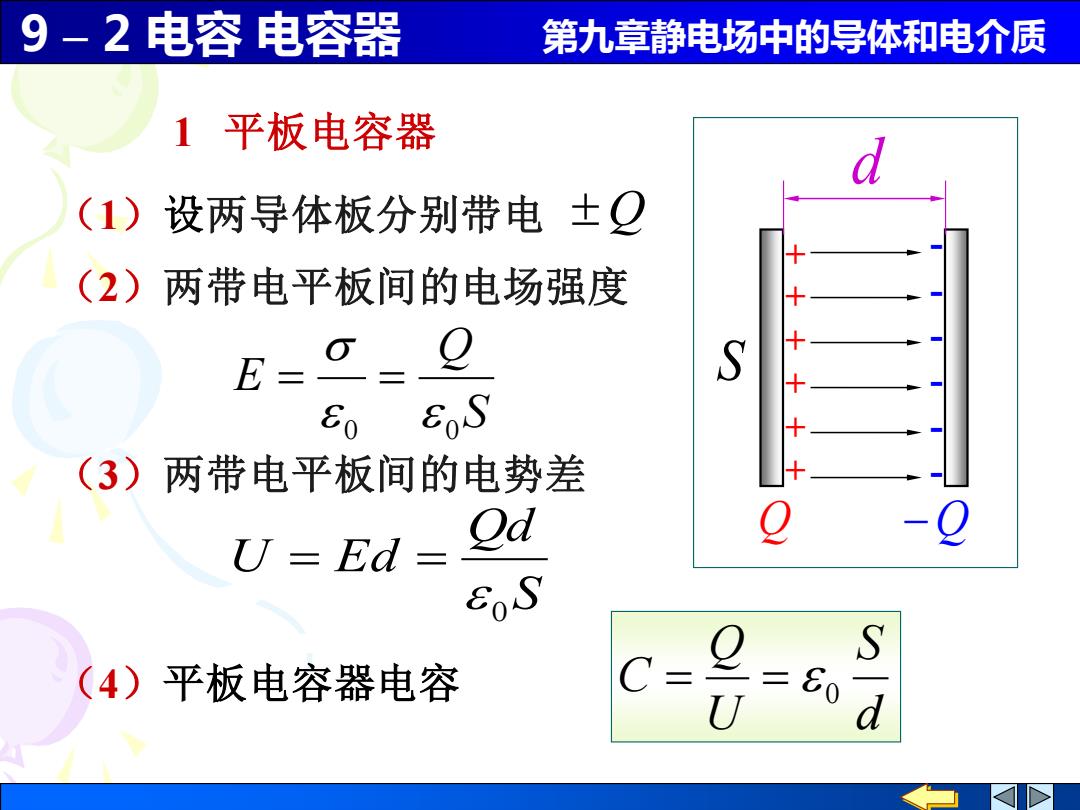
9 – 2 电容 电容器 第九章静电场中的导体和电介质 d S 1 平板电容器 + + + + + + Q −Q - - - - - - S Q E 0 0 = = (2)两带电平板间的电场强度 (1)设两导体板分别带电 Q S Qd U Ed 0 = = (3)两带电平板间的电势差 d S U Q C 0 (4)平板电容器电容 = =

9-2电容电容器 第九章静电场中的导体和电介质 例1平行平板电容器的极板是边长为1的正方 形,两板之间的距离d=lmm.如两极板的电势差 为100V,要使极板上储存±104C的电荷,边长1 应取多大才行. 104 解 C-0 F=10-6F U 100 S=12 Cd 1= =10.6m Eo
9 – 2 电容 电容器 第九章静电场中的导体和电介质 例1 平行平板电容器的极板是边长为 的正方 形,两板之间的距离 .如两极板的电势差 为 ,要使极板上储存 的电荷,边长 应取多大才行. l d =1mm 100V 10 C −4 l 解 F 10 F 100 10 6 4 − − = = = U Q C 2 S = l 10.6m 0 = = Cd l
9-2电容电容器 第九章静电场中的导体和电介质 2圆柱形电容器 (1)设两导体圆柱面单位长度上 1>>RB 分别带电士入 (2)E= 入 -,(R4<r<RB) 2元6 (3)U= 个Rdr RB JRA2元8Or 2π801 RA (4电溶C-号-2rs R d=R,-R,<R,C≈2πeR= EoS 平行板电 d d 容器电容
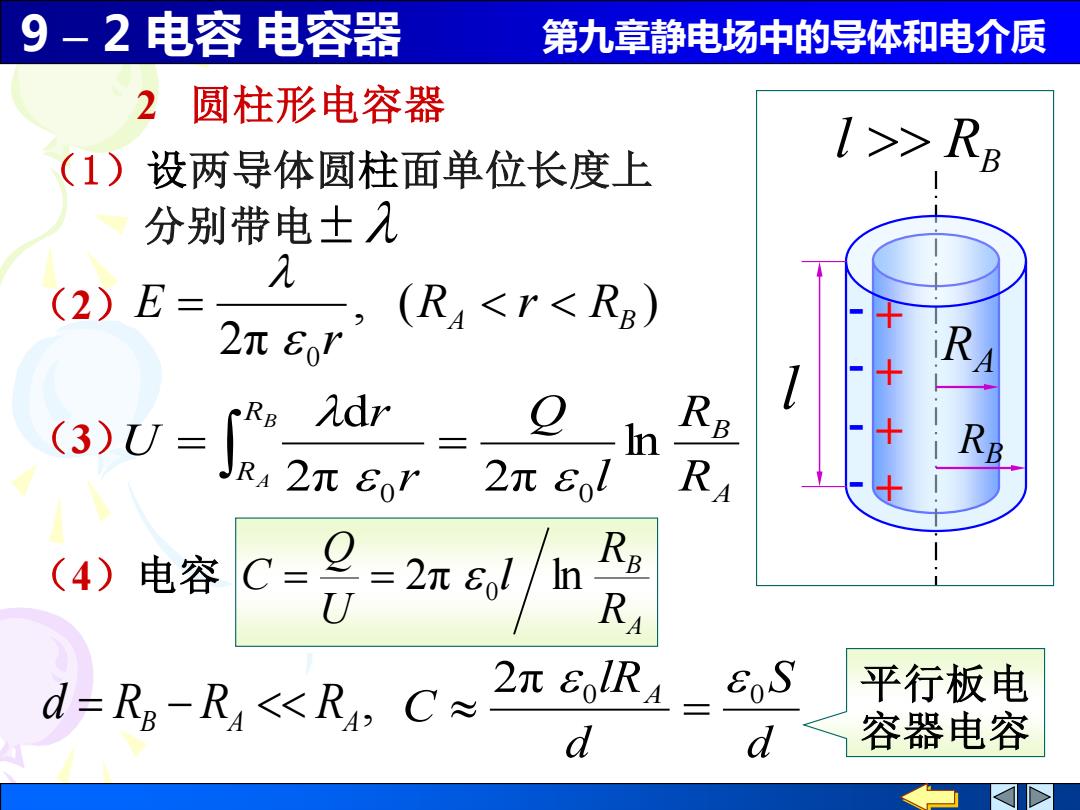
9 – 2 电容 电容器 第九章静电场中的导体和电介质 RA RB l RB l 平行板电 容器电容 2 圆柱形电容器 , RB RA RA d = − d S d lR C 2π 0 A 0 = A B R R l U Q C = = 2π 0 ln A B R R R R l Q r r U B A ln 2π 2π d 0 0 = = ( 3) , ( ) 2π 0 A RB R r r E = (2) (4)电容 + + + + - - - - (1)设两导体圆柱面单位长度上 分别带电