
散列函数的要求 ·H能用于任意大小的分组; ·H能产生定长的输出; 0 对任何给定的x,H(x)要相对易于计算,使得硬件和软件 实现成为实际可能; 0 对任何给定的码h,寻找x使得H(x)=h在计算上是不可 行的,即单向性(one-way); 对任意给定的分组x,寻找不等于x的y,使得H(x)=Hy) 在计算上是不可行的,即弱抗冲突性(Weak Collision-free); 。 找到任何满足x)三Hy)的一对数(x,y),在计算上是不 可行的,即强抗冲突性(Strong Collision-free); 7
散列函数的要求 • H 能用于任意大小的分组; • H 能产生定长的输出; • 对任何给定的 x,H(x )要相对易于计算,使得硬件和软件 实现成为实际可能; • 对任何给定的码 h ,寻找 x 使得 H(x ) =h 在计算上是不可 行的,即单向性 (one-way); • 对任意给定的分组 x,寻找不等于x 的 y,使得 H(x ) = H(y ) 在计算上是不可行的 在计算上是不可行的,即弱抗冲突性 (Weak Collision Weak Collision -free); • 找到任何满足 H(x ) =H (y )的一对数 (x, y),在计算上是不 可行的,即强抗冲突性 (Strong Collision-free); 7

提纲 ·1散列函数 -1.1散列函数的定义 -1.2散列函数的通用结构 -1.3MD5 ·2消息认证码 8
提纲 • 1 散列函数 – 1.1 散列函数的定义 – 1.2 散列函数的通用结构 – 1 3 MD5 1.3 MD5 • 2 消息认证码 8

2.2Hash函数的通用结构 ·由Ron Rivest于1990年提出MD4 ·几乎被所有Hash函数使用 ·具体做法: -把原始消息M分成一些固定长度的块Y, -最后一块padding并使其包含消息M长度 - 设定初始值CV 压缩函数fCV,=f(CV,Y1) CBC模式(Cipher Block Chaining) -最后一个CV,为Hash值 填充100.0,使其<长度>=448mod512,然后再加上以64bits表示的Message长度。例message 1en=13096bits,则填充串“100.0”,长度为448-mod(13096,512)=152,即1后面跟151个0, 然后再填充13096的646its表示(长度):0.011001100101000
2.2 Hash函数的通用结构 函数的通用结构 • 由R Ri onvest于1990年提出MD4 • 几乎被所有Hash函数使用 • 具体做法: – 把原始消息M分成一些固定长度的块Yi – 最后一块 padding 并使其包含消息M长度 – 设定初始值CV0 – 压缩函数 f CVi=f (CVi 1 Yi 1 压缩函数 f, CV ) i=f (CVi-1, Yi-1) – 最后一个 CVi 为Hash值 9 CBC模式(Cipher Block Chaining) 填充100...0,使其<长度> ≡448 mod 512,然后再加上以64bits表示的Message长度。例如 message len=13096bits, 则填充串“100...0”,长度为448-mod(13096,512)=152,即1后面跟151个0, 然后再填充13096的64bits表示(长度): 0...0 11001100101000
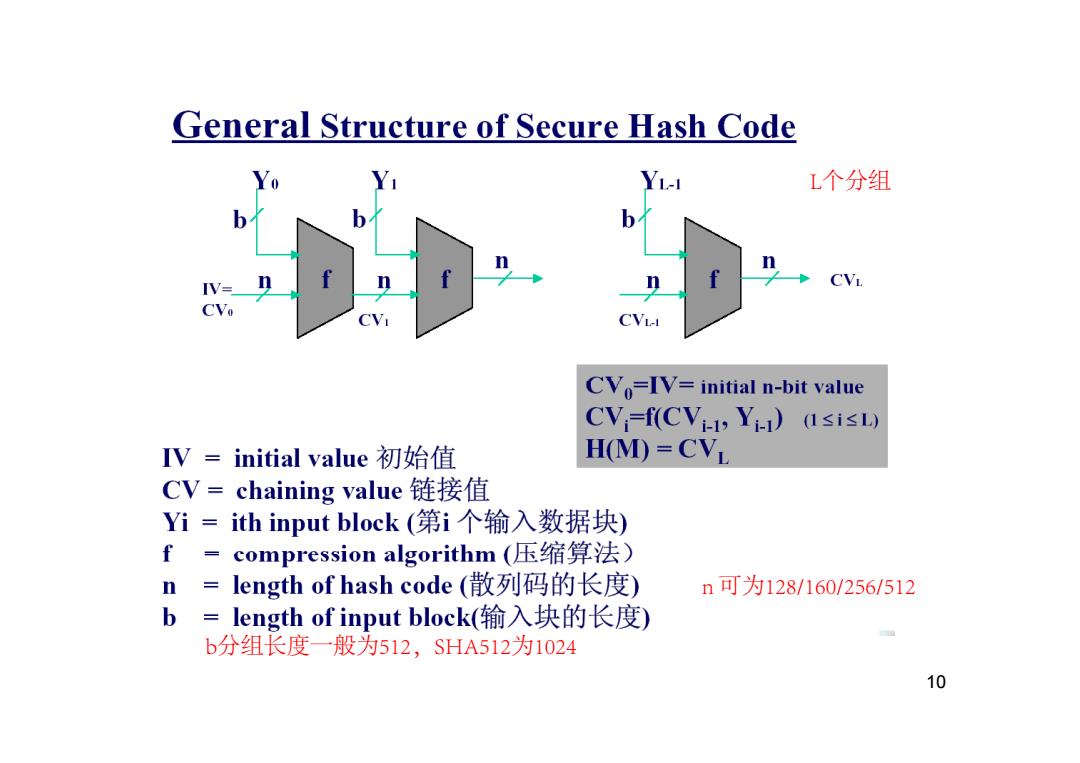
General Structure of Secure Hash Code YL- L个分组 CVo=IV=initial n-bit value CVi=f(CVi-,Yi1) (1≤i≤L) IV=initial value初始值 H(M)=CVL CV=chaining value链接值 Yi=ith input block(第i个输入数据块) f-compression algorithm(压缩算法) n=length of hash code(散列码的长度) n可为128/160/256/512 b=length of input block(输入块的长度) b分组长度一般为512,SHA512为1024 10
10 L个分组 n 可为128/160/256/512 b分组长度一般为512,SHA512为1024

提纲 ·1散列函数 -1.1散列函数的定义 -1.2散列函数的通用结构 -1.3MD5 ·2消息认证码 11
提纲 • 1 散列函数 – 1.1 散列函数的定义 – 1.2 散列函数的通用结构 – 1 3 MD5 1.3 MD5 • 2 消息认证码 11