
方差分析的基本思想和原理 (均方一MS) 1.平方和除以相应的自由度 2.若原假设成立,组间均方与组内均方的数值就 应该很接近,它们的比值就会接近1 3:若原假设不成立,组间均方会大于组内均方, 它们之间的比值就会大于1 4. 当这个比值大到某种程度时,就可以说不同水 平之间存在着显著差异,即自变量对因变量有影 响 判断行业对投诉次数是否有显著影响,也就是检验被 投诉次数的差异主要是由于什么原因所引起的。如果 这种差异主要是系统误差,说明不同行业对投诉次数 有显著影响
10 - 17 作者:贾俊平,中国人民大学统计学院 统计学 STATISTICS (第7版) 方差分析的基本思想和原理 (均方—MS) 1. 平方和除以相应的自由度 2. 若原假设成立,组间均方与组内均方的数值就 应该很接近,它们的比值就会接近1 3. 若原假设不成立,组间均方会大于组内均方, 它们之间的比值就会大于1 4. 当这个比值大到某种程度时,就可以说不同水 平之间存在着显著差异,即自变量对因变量有影 响 § 判断行业对投诉次数是否有显著影响,也就是检验被 投诉次数的差异主要是由于什么原因所引起的。如果 这种差异主要是系统误差,说明不同行业对投诉次数 有显著影响

统计学 STATISTICS (第7版) 方差分析的基本假定 10-18 作准青得中,中人民人分愿时糖
10 - 18 作者:贾俊平,中国人民大学统计学院 统计学 STATISTICS (第7版) 方差分析的基本假定

方差分析的基本假定 1.每个总体都应服从正态分布 ·对于因素的每一个水平,其观察值是来自服从正 态分布总体的简单随机样本 ·比如,每个行业被投诉的次数必须服从正态分布 2.各个总体的方差必须相同 ·各组观察数据是从具有相同方差的总体中抽取的 ·比如,4个行业被投诉次数的方差都相等 3. 观察值是独立的 比如,每个行业被投诉的次数与其他行业被投诉 的次数独立
10 - 19 作者:贾俊平,中国人民大学统计学院 统计学 STATISTICS (第7版) 方差分析的基本假定 1. 每个总体都应服从正态分布 § 对于因素的每一个水平,其观察值是来自服从正 态分布总体的简单随机样本 § 比如,每个行业被投诉的次数必须服从正态分布 2. 各个总体的方差必须相同 § 各组观察数据是从具有相同方差的总体中抽取的 § 比如,4个行业被投诉次数的方差都相等 3. 观察值是独立的 § 比如,每个行业被投诉的次数与其他行业被投诉 的次数独立

方差分析中的基本假定 1.在上述假定条件下,判断行业对投诉次数是否 有显著影响,实际上也就是检验具有同方差的 4个正态总体的均值是否相等 2.如果4个总体的均值相等,可以期望4个样本的 均值也会很接近 ■4个样本的均值越接近,推断4个总体均值相等的 证据也就越充分 ·样本均值越不同,推断总体均值不同的证据就越 充分
10 - 20 作者:贾俊平,中国人民大学统计学院 统计学 STATISTICS (第7版) 方差分析中的基本假定 1. 在上述假定条件下,判断行业对投诉次数是否 有显著影响,实际上也就是检验具有同方差的 4个正态总体的均值是否相等 2. 如果4个总体的均值相等,可以期望4个样本的 均值也会很接近 § 4个样本的均值越接近,推断4个总体均值相等的 证据也就越充分 § 样本均值越不同,推断总体均值不同的证据就越 充分
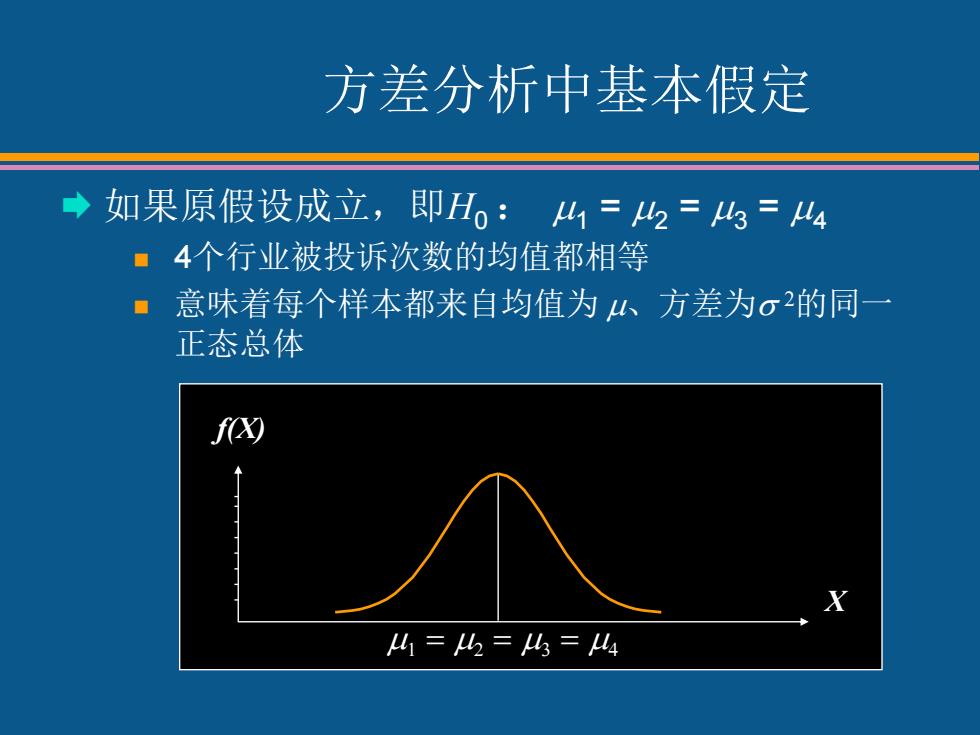
方差分析中基本假定 → 如果原假设成立,即Ho:4=2=%=4 ■4个行业被投诉次数的均值都相等 ■意味着每个样本都来自均值为山、方差为σ2的同一 正态总体 山1=4=4=44
10 - 21 作者:贾俊平,中国人民大学统计学院 统计学 STATISTICS (第7版) 方差分析中基本假定 如果原假设成立,即H0 : 1 = 2 = 3 = 4 n 4个行业被投诉次数的均值都相等 n 意味着每个样本都来自均值为、方差为2的同一 正态总体 X f(X) 1 2 3 4