
Logic Connectives p q p→q T T T T F F F T T Implication F T p-→q All possible values of <p,g> If p then q” p:2+3=6. q:n is a rational number p→q:lF2+3=6,THENπis a rational number
Logic Connectives Implication 𝒑 → 𝒒 “If 𝒑 then 𝒒” 𝑝 𝑞 𝑝 → 𝑞 T T T T F F F T T F F T 𝑝: 2+3=6. 𝑞: 𝜋 is a rational number 𝑝 → 𝑞: IF 2+3=6, THEN 𝜋 is a rational number. All possible values of < 𝑝, 𝑞 >
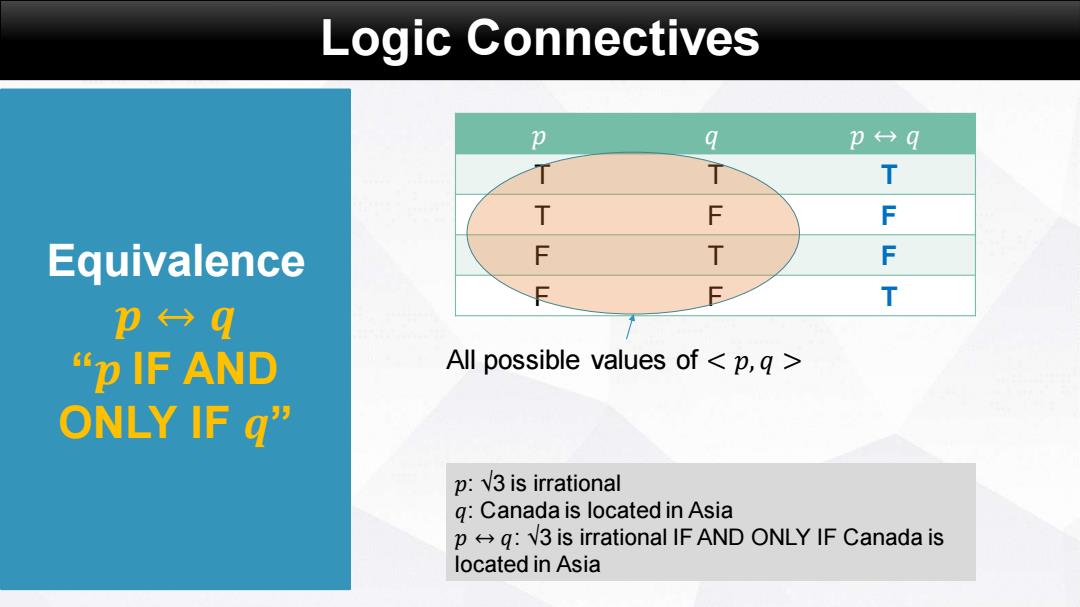
Logic Connectives p q 卫←→q T T T T F F Equivalence F T F E T pq p IF AND All possible values of <p,g ONLY IF g” p:3 is irrational q:Canada is located in Asia pq:3 is irrational IF AND ONLY IF Canada is located in Asia
Logic Connectives Equivalence 𝒑 ↔ 𝒒 “𝒑 IF AND ONLY IF 𝒒” 𝑝 𝑞 𝑝 ↔ 𝑞 T T T T F F F T F F F T 𝑝: √3 is irrational 𝑞: Canada is located in Asia 𝑝 ↔ 𝑞: √3 is irrational IF AND ONLY IF Canada is located in Asia All possible values of < 𝑝, 𝑞 >

Compared with Connectives in Natural Language English 中文 Logic not... 不是.… 7 ...and... .并且 Λ ...Or... 或者. V either...or...,but not both 不是.就是. ⊕ if...then... 如果..那么.… if and only if 当且仅当 ←→ For every logic connective,a counterpart having ALMOST the same semantics can be found in natural language. The semantic of a logic connective is rigorous defined by the corresponding TRUTH TABLE
Compared with Connectives in Natural Language English 中文 Logic not… 不是… ¬ …and… …并且… ⋀ …or… …或者… ⋁ either…or…, but not both 不是…就是… ⊕ if…then… 如果…那么… → if and only if 当且仅当 ↔ For every logic connective, a counterpart having ALMOST the same semantics can be found in natural language. The semantic of a logic connective is rigorous defined by the corresponding TRUTH TABLE

Truth Table of Proposition Formula (p∧q)→r p q r p pq r (-p∧q)→r 000 1 0 1 1 001 1 0 0 1 010 1 1 1 1 011 1 1 0 0 100 1 0 1 1 101 1 0 0 1 110 1 0 1 1 111 1 0 0 1 All Possible Assignments
Truth Table of Proposition Formula ¬𝑝 ∧ 𝑞 → ¬𝑟 𝒑 𝒒 𝒓 ¬𝒑 ¬𝒑 ∧ 𝒒 ¬𝒓 ¬𝒑 ∧ 𝒒 → ¬𝒓 0 0 0 1 0 1 1 0 0 1 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 1 0 0 1 0 0 1 0 1 1 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0 0 1 All Possible Assignments

Special Logic Formula Tautology Contradiction Satisfiable (重言式,永真式) (矛盾式,永假式) Formula (可能式,可满足式) ·Always TRUE for all ·Always FALSE for all ·Can be TRUE for some possible assignments possible assignments possible assignments (p→q)→(q→p) pΛp (p→q)pVq)
Special Logic Formula • Always TRUE for all possible assignments (𝒑 → 𝒒) ⟷ (¬𝒒 → ¬𝒑) Tautology (重言式,永真式) • Always FALSE for all possible assignments 𝒑 ∧ ¬𝒑 Contradiction (矛盾式,永假式) • Can be TRUE for some possible assignments (𝒑 → 𝒒) ∧ (𝒑 ∨ 𝒒) Satisfiable Formula (可能式,可满足式)