
12.2 一次回归正交设计 12.2.1 一次回归正交设计 建立一次回归方程的回归设计方法有多种,这里介绍一种常 用的方法,它是利用二水平正交表来安排试验的设计方法。 其主要步骤如下: 1.确定因子水平的变化范围 设影响指标y的因子有p个 ,希望通过试验建立y 关于 的一次回归方程,那么首先要确定每个因子的变 化范围,设因子 的取值范围为: , 这里 与 分别是因子 的下水平与上水平。 p z ,z , ,z 1 2 p z ,z , ,z 1 2 j j j z z z 1 2 j z1 j z2 j z j = 1,2, , p
12.2 一次回归正交设计 12.2.1 一次回归正交设计 建立一次回归方程的回归设计方法有多种,这里介绍一种常 用的方法,它是利用二水平正交表来安排试验的设计方法。 其主要步骤如下: 1.确定因子水平的变化范围 设影响指标y的因子有p个 ,希望通过试验建立y 关于 的一次回归方程,那么首先要确定每个因子的变 化范围,设因子 的取值范围为: , 这里 与 分别是因子 的下水平与上水平。 p z ,z , ,z 1 2 p z ,z , ,z 1 2 j j j z z z 1 2 j z1 j z2 j z j = 1,2, , p

2.对每一因子的水平进行编码 记因子 的零水平为 其变化半径为 那么采用如下编码式,即 , 对因子的水平进行编码,常列成如下的因子水平编码表: z0 j = (z1 j + z2 j )/ 2 j z j = (z2 j − z1 j )/ 2 j j j j z z x − = 0 j = 1,2, , p
2.对每一因子的水平进行编码 记因子 的零水平为 其变化半径为 那么采用如下编码式,即 , 对因子的水平进行编码,常列成如下的因子水平编码表: z0 j = (z1 j + z2 j )/ 2 j z j = (z2 j − z1 j )/ 2 j j j j z z x − = 0 j = 1,2, , p

3.选择适当的二水平正交表安排试验 在用二水平正交安排试验时,要用“-1”代换通常二水平正 交表中的“2”,以适应因子水平编码的需要。这样一来,正 交表中的“1”与“-1”不仅表示因子水平的不同状态,也表示 了因子水平的数量大小。经过这样的代换后,正交表的交互 作用列可以由表中相应列的对应元素相乘得到,从而交互作 用列表也不需要了。 表12.2.2就是一张代换后的L8 (27 ),与原来的正交表没有本 质区别,仍然用L8 (27 )表示
3.选择适当的二水平正交表安排试验 在用二水平正交安排试验时,要用“-1”代换通常二水平正 交表中的“2”,以适应因子水平编码的需要。这样一来,正 交表中的“1”与“-1”不仅表示因子水平的不同状态,也表示 了因子水平的数量大小。经过这样的代换后,正交表的交互 作用列可以由表中相应列的对应元素相乘得到,从而交互作 用列表也不需要了。 表12.2.2就是一张代换后的L8 (27 ),与原来的正交表没有本 质区别,仍然用L8 (27 )表示
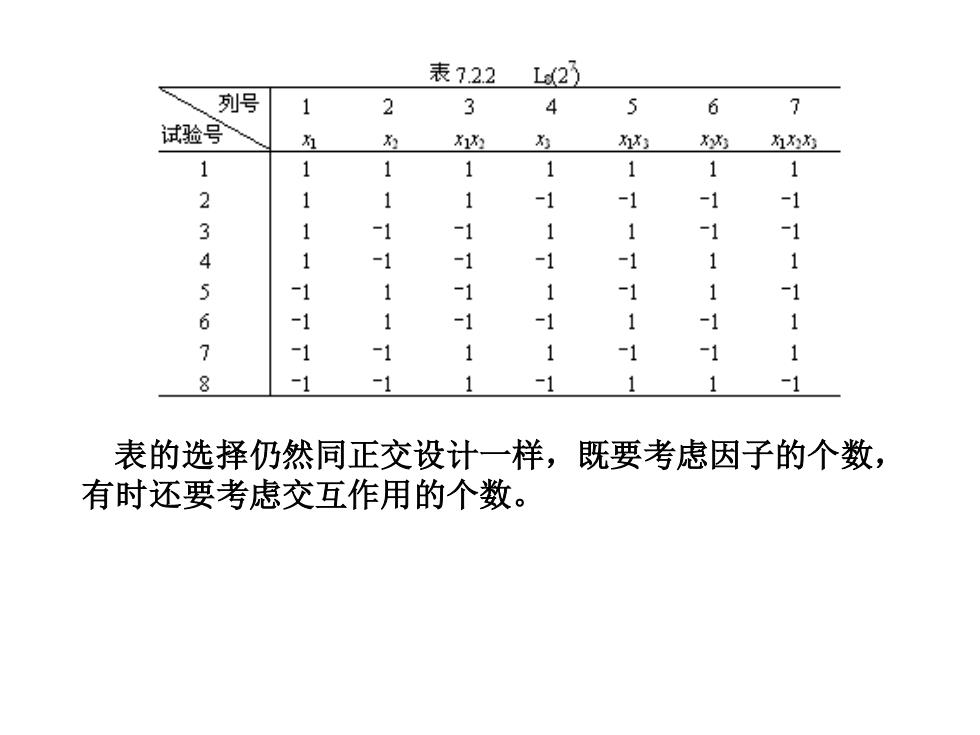
表的选择仍然同正交设计一样,既要考虑因子的个数, 有时还要考虑交互作用的个数
表的选择仍然同正交设计一样,既要考虑因子的个数, 有时还要考虑交互作用的个数

在改造后的正交表中,若用 表示第i号试验第j个因子xj的 取值,那么 称具有上述性质的设计称为正交设计。 x j , , , p n i ij 0 1 2 1 = = = , x x i j i, j , , , p n k ki kj 0 1 2 1 = = = , , ij x
在改造后的正交表中,若用 表示第i号试验第j个因子xj的 取值,那么 称具有上述性质的设计称为正交设计。 x j , , , p n i ij 0 1 2 1 = = = , x x i j i, j , , , p n k ki kj 0 1 2 1 = = = , , ij x