
信息检索与数据挖掘 2019/5/516 EM算法:迭代逼近最优解过程分析 p(X;θ)=∑zp(X,Z;)←从联合概率计算边缘概率 p0=∑9 p(,Z;0) ←q(Z)=p(Z1X;),构造的先验分布 q(Z) p(X,Z ;0) q(Z) -Jensen's inequality logp(X:0)≥∑92;6r1og (x,Z;0) q(2;0t) 1ogpX;)≥∑n(2Ix;0)1og (X,Z;0) (ZX;0) wx,6=∑ax:6ew的时 p(x,z;0)p(Zx;0) gw:≥∑a6的+∑t09 logp(XI0)≥c(q,0)+KL(q‖p)
信息检索与数据挖掘 2019/5/5 16 𝑝 𝑋 ; 𝜃 = σ𝑍 𝑝 𝑋, 𝑍 ; 𝜃 ←从联合概率计算边缘概率 𝑝(𝑋 ; 𝜃) = 𝑍 𝑞 𝑍 𝑝 𝑋, 𝑍 ; 𝜃 𝑞(𝑍) , ← 𝑞 𝑍 = 𝑝(𝑍|𝑋 ; 𝜃𝑡 ),构造的先验分布 log 𝑝(𝑋 ; 𝜃) = log 𝑍 𝑞 𝑍 𝑝 𝑋, 𝑍 ; 𝜃 𝑞(𝑍) ≥ 𝑍 𝑞 𝑍 log 𝑝 𝑋, 𝑍 ; 𝜃 𝑞 𝑍 ← 𝐽𝑒𝑛𝑠𝑒𝑛 ′ 𝑠 𝑖𝑛𝑒𝑞𝑢𝑎𝑙𝑖𝑡𝑦 log 𝑝(𝑋 ; 𝜃) ≥ 𝑍 𝑞 𝑍 ; 𝜃መ 𝑡 log 𝑝 𝑋, 𝑍 ; 𝜃መ 𝑡 𝑞 𝑍; 𝜃መ 𝑡 log 𝑝(𝑋 ; 𝜃) ≥ 𝑍 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 log 𝑝 𝑋, 𝑍 ; 𝜃መ 𝑡 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 log 𝑝(𝑋 ; 𝜃) ≥ 𝑍 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 log 𝑝 𝑋, 𝑍 ; 𝜃መ 𝑡 𝑝 𝑍|𝑋 ; 𝜃መ ∗ 𝑝 𝑍|𝑋 ; 𝜃መ ∗ 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 log 𝑝(𝑋 ; 𝜃) ≥ 𝑍 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 log 𝑝 𝑋, 𝑍 ; 𝜃መ 𝑡 𝑝 𝑍|𝑋 ; 𝜃መ ∗ + 𝑍 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 log 𝑝 𝑍|𝑋 ; 𝜃መ ∗ 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 → 𝒍𝒐𝒈𝒑 𝑿 𝜽 ≥ 𝓛 𝒒, 𝜽 + 𝑲𝑳(𝒒 ∥ 𝒑) EM算法:迭代逼近最优解过程分析

信息检索与数据挖掘 2019/5/517 EM算法:迭代逼近最优解过程示意 logp(Xl0)=L(q,0)+KL(q ll p) Expectation:参数0=t固定,使KL(q‖p)最小化,即更新后验概率p(ZIX;) Maximization:使C(g,0)最大化,即更新参数t+1=0t new log likelihood Inp(y8(1)) KL )(xy()) E step makes the new lower bound lower bound tight F(Q),0()) log likelihood In p(ye(t)) Inp(y (t)) (f).o(t)) KL [K)p(x1y.0())]=0 KL [)p(xy() ow台bound LF(),()) “=5三15 E step M step 关于EM算法的九层境界的浅薄介绍http://www.elecfans.com/d/604076.html
信息检索与数据挖掘 2019/5/5 17 EM算法:迭代逼近最优解过程示意 log 𝑝 𝑋 𝜃 ≥ ℒ 𝑞, 𝜃 + 𝐾𝐿 𝑞 ∥ 𝑝 Expectation:参数𝜃 = 𝜃መ 𝑡固定,使𝐾𝐿 𝑞 ∥ 𝑝 最小化,即更新后验概率𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 Maximization: 使ℒ 𝑞, 𝜃 最大化,即更新参数𝜃መ 𝑡+1=𝜃መ 𝑡 关于EM算法的九层境界的浅薄介绍 http://www.elecfans.com/d/604076.html
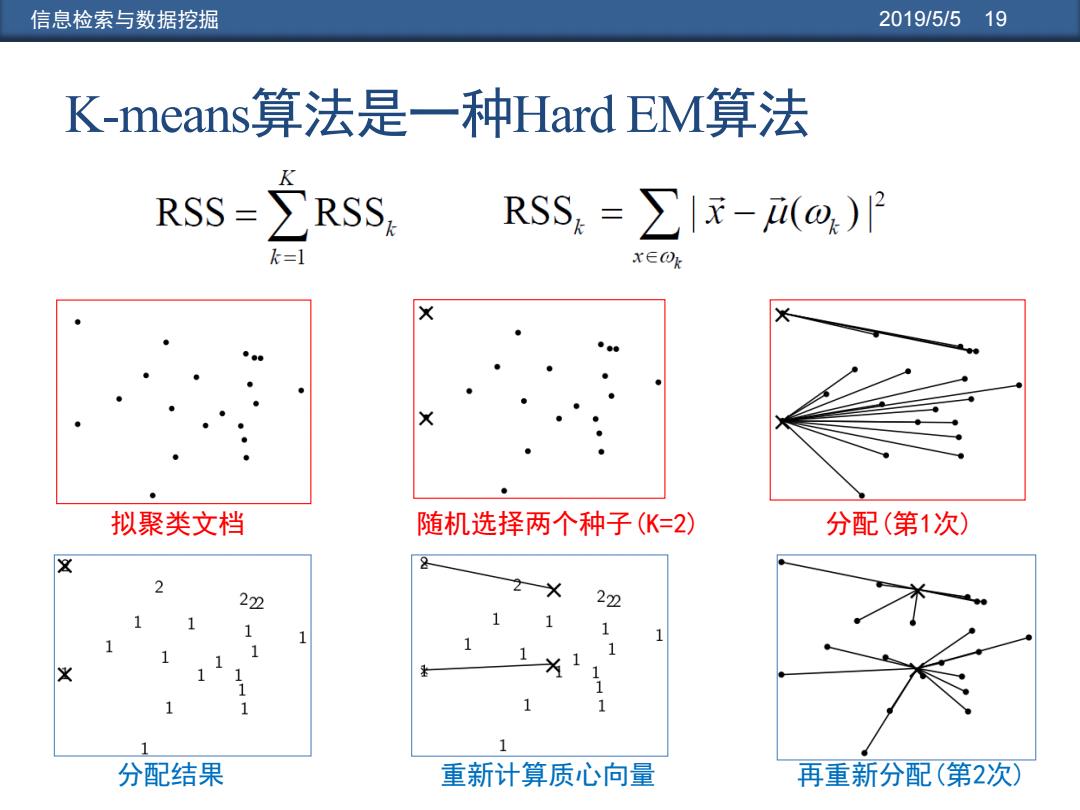
信息检索与数据挖掘 2019/5/519 K-means?算法是一种Hard EM算法 RSS=RSS ,RSS=∑|元-(ω)月 k=1 x∈Ok 拟聚类文档 随机选择两个种子(K=2) 分配(第1次) 222 22 1 1 分配结果 重新计算质心向量 再重新分配(第2次)
信息检索与数据挖掘 2019/5/5 19 K-means算法是一种Hard EM算法 分配结果 重新计算质心向量 再重新分配(第2次) 拟聚类文档 随机选择两个种子(K=2) 分配(第1次)

信息检索与数据挖掘 2019/5/520 K-neans算法是一种Hard EM2算法 X=(x1,X2,…,xN),X为第i个文档 Z=(Z1,Z2,…,zN),2E{ω1,ω2,…,ωK}Z为隐变量,代表文档x所属的类 参数0=(O1,02,,0K)∈{u(ω1)4(ω2),…,4(ωK)},代表类的质心 w:o=oz,09n202 3q(Z,0) gminxi0 Expectation:q(z;)=p(zX;)= →P(Z=zlX=x;0) p(x,z;6t)= 四pK=2=:的 Maximization: 上述形式化韬述受如下文献的启发导出,与该文并不相同,仅供参考 关于EM算法的九层境界的浅薄介绍http.ww.elecfans.com/d/604076.html
信息检索与数据挖掘 2019/5/5 20 K-means算法是一种Hard EM算法 𝑥 = 𝑥1, 𝑥2, … , 𝑥𝑁 , xi为第i个文档 𝑧 = 𝑧1, 𝑧2, … , 𝑧𝑁 , 𝑧𝑖 ∈ {𝜔1, 𝜔2, … , 𝜔𝐾} zi为隐变量,代表文档xi所属的类 参数𝜃 = (𝜃1, 𝜃2, … , 𝜃𝐾) ∈ {𝜇(𝜔1), 𝜇(𝜔2), … , 𝜇(𝜔𝐾)} ,代表类的质心 ℒ(𝑋 ; 𝜃) = 𝑍 𝑞 𝑍 ; 𝜃መ 𝑡 log 𝑝 𝑋, 𝑍 ; 𝜃መ 𝑡 𝑞 𝑍; 𝜃መ 𝑡 Expectation:𝑞 𝑍 ; 𝜃መ 𝑡 = 𝑝(𝑍|𝑋 ; 𝜃መ 𝑡 ) argmin 𝑗 𝑥𝑖−𝜃 𝑗 𝑡 𝑃(𝑍 = 𝑧𝑗 |𝑋 = 𝑥𝑖 ; 𝜃መ 𝑡 ) 𝑝 𝑋, 𝑍 ; 𝜃መ 𝑡 argmin 𝑗 𝑥𝑖−𝜃 𝑗 𝑡 𝑃 𝑋 = 𝑥𝑖 , 𝑍 = 𝑧𝑗 ; 𝜃መ 𝑡 Maximization:𝜃መ 𝑗 𝑡+1 = 1 |𝜔𝑗 | σ𝑧𝑖∈𝜔𝑗 𝑥𝑖 上述形式化描述受如下文献的启发导出,与该文并不相同,仅供参考 关于EM算法的九层境界的浅薄介绍 http://www.elecfans.com/d/604076.html

信息检索与数据挖掘 1 01r*2 小结:EM log P(x;0) (Expectation Maximization) 0*1 80 ·参数估计的两种情形 ·完全信息下的MLE估计 ·不完全信息下的参数估计 9: ·EM算法是一种解决存在隐含变量优化问题的方法 ·E-Step:根据已经估计的参数计算隐藏变量的后验概率 ( 即根据参数计算似然函数的期望) ·M-Step:根据已经计算的后验概率更新参数(选择参数 使似然最大化) •特点 KL(qllp) 。通过不断构造下界逐步向最优逼近 ·K-means2算法是一种Hard EM.算法 c(q,8) Inp(X 0) ·估计参数的初值影响到是否落入局部最优点 C.B.Do and S.Batzoglou,"What is the expectation maximization algorithm?,"Nature Biotechnology,vol.26,p.897,08/01/online 2008. 关于EM算法的九层境界的浅薄介绍http:wwMw.elecfans.com/d/604076.html
信息检索与数据挖掘 2019/5/5 21 小结:EM (Expectation Maximization) • 参数估计的两种情形 • 完全信息下的MLE估计 • 不完全信息下的参数估计 • EM算法是一种解决存在隐含变量优化问题的方法 • E-Step:根据已经估计的参数计算隐藏变量的后验概率( 即根据参数计算似然函数的期望) • M-Step:根据已经计算的后验概率更新参数(选择参数 使似然最大化) • 特点 • 通过不断构造下界逐步向最优逼近 • K-means算法是一种Hard EM算法 • 估计参数的初值影响到是否落入局部最优点 C. B. Do and S. Batzoglou, "What is the expectation maximization algorithm?," Nature Biotechnology, vol. 26, p. 897, 08/01/online 2008. 关于EM算法的九层境界的浅薄介绍 http://www.elecfans.com/d/604076.html