
信息检索与数据挖掘 2019/5/511 今日内容:数据挖掘经典算法概述 ·教材中有的 ·Naive Bayes、EM、K-means、SVM、kNN ·决策树 ·ID3 。C4.5 ·CART ·把若干个分类器整合为一个分类器 ·Bagging ·Boosting ·AdaBoost,1995 ·流数据挖掘:频繁项集 。Web中的数据挖掘
信息检索与数据挖掘 2019/5/5 11 今日内容:数据挖掘经典算法概述 • 教材中有的 • Naive Bayes、 EM、K-means、SVM、kNN • 决策树 • ID3 • C4.5 • CART • 把若干个分类器整合为一个分类器 • Bagging • Boosting • AdaBoost,1995 • 流数据挖掘:频繁项集 • Web中的数据挖掘

信息检索与数据挖掘 2019/5/512 EM算法示例:求两个硬币随机抛出后正反面的概率 完全信息下的MLE估计 x=(x,,,x),x,∈{0,l,…,10}第i次抛硬币试验中正面head)朝上的次数 z=(31,22,…,25),二,∈{A,B}第次抛硬币试验中被抛掷的硬币是A还是B a Maximum likelihood x=(5,9,8,4,7) Coin A Coin B =(B,A,A,B,A) HTTTHHTHTH 5H,5T 24 HHHHTHHHHH 9H,1T 0 24+6=0.80 HTHHHHHTHH 8H,2T 9 HTHTTTHHTT 4H,6T A=g+17=0.45 THHHTHHHTH 7H,3T 24H,6T 9H,11T 5 sets,10 tosses per set MLE:Find parameters =(,0g)that maximize logP(x,z;0) 找到使得1ogP(x,z,0)最大的参数0,logP(x,z,0)分号左边是随机变量,右边是模型参数 04= 硬币A正面朝上的次数,可。= 硬币B正面朝上的次数 硬币A抛的总次数 硬币B抛的总次数 C.B.Do and S.Batzoglou,"What is the expectation maximization algorithm?,"Nature Biotechnology,vol.26,p.897,08/01/online 2008
信息检索与数据挖掘 2019/5/5 12 EM算法示例:求两个硬币随机抛出后正反面的概率 完全信息下的MLE估计 C. B. Do and S. Batzoglou, "What is the expectation maximization algorithm?," Nature Biotechnology, vol. 26, p. 897, 08/01/online 2008. MLE:Find parameters 𝜃መ = (𝜃መ 𝐴 , 𝜃መ 𝐵 ) that maximize logP(x,z;θ). 找到使得logP(x,z;θ)最大的参数 θ,logP(x,z ; θ) 分号左边是随机变量,右边是模型参数 𝜃መ 𝐴 = 硬币𝐴正面朝上的次数 硬币𝐴抛的总次数 ,𝜃መ 𝐵 = 硬币B正面朝上的次数 硬币B抛的总次数 x = (x1, x2, …, x5), xi ∈ {0,1,…,10} 第i次抛硬币试验中正面(head)朝上的次数 z = (z1 , z2 ,…, z5 ), zi ∈ {A,B} 第i次抛硬币试验中被抛掷的硬币是A还是B x=(5,9,8,4,7) z=(B,A,A,B,A)
信息检索与数据挖掘 2019/5/513 M算法示例:求两个硬币随机抛出后正反面的慨率 不完全信息:不知道每次抛的是A还是B 9H1T→0.80*9H1T+0.20*9H1T Expectation maximization 如果是A硬币,抛出 →7.2H,0.8T+1.8H,0.2T E-step →0A= 7.2 1.8 HHHHTHHHHH的概率是,(1- 04)=0.69×0.41=0.010077696×0.4 7.2+0.8 1.8+0.2 Coin A Coin B ≈0.004 T下THTNTN 0.45X 0.55X =2.2H.2.2T ≈2.8H,2.8T 如果是B硬币,抛出 HHHHTHHHHH ■日s8gg▣■88gggg88无8日88g。9”。目””” ,0.80X 0.20X ≈7.2H,0.8T ≈1.8H,02T HHHHTHHHHH的概率是0,(1- HTHTTTHHTT 884g”1t88g88gg 0.73x 0.27X =5.9H,1.5T =2.1H,0.5T 0g)1=0.510≈0.001 035X 0.65X =1.4H,2.1T =2.6H,3.9T =0.60 0.65× 0.35X =4.5H,1.9T =2.5H,11T 日850 =21.3H,8.6T =11.7H,8.4T 故这次试验是硬币A的期望为 21.3 0.004/(0.004+0.001)=0.80,是硬币B 0213+8.60.71 M-step 的期望为0.004/(0.004+0.001)=0.20 11.7 60-m+840.58 60=0.80 6=0.52 1.EM starts with an initial guess of the parameters. 2.In the E-step,a probability distribution over possible completions is computed using the current parameters.The counts shown in the table are the expected numbers of heads and tails according to this distribution. 3.In the M-step,new parameters are determined using the current completions. 4.After several repetitions of the E-step and M-step,the algorithm converges. C.B.Do and S.Batzoglou,"What is the expectation maximization algorithm?,"Nature Biotechnology,vol.26,p.897,08/01/online 2008
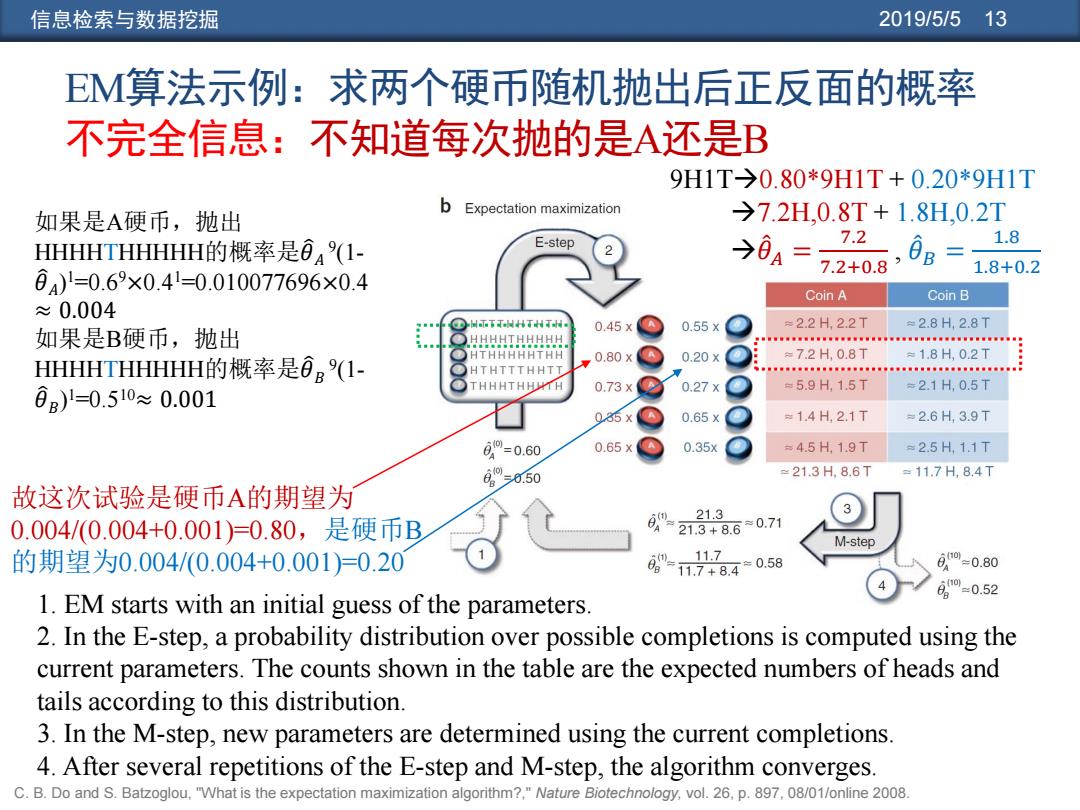
信息检索与数据挖掘 2019/5/5 13 EM算法示例:求两个硬币随机抛出后正反面的概率 不完全信息:不知道每次抛的是A还是B 1. EM starts with an initial guess of the parameters. 2. In the E-step, a probability distribution over possible completions is computed using the current parameters. The counts shown in the table are the expected numbers of heads and tails according to this distribution. 3. In the M-step, new parameters are determined using the current completions. 4. After several repetitions of the E-step and M-step, the algorithm converges. 故这次试验是硬币A的期望为 0.004/(0.004+0.001)=0.80,是硬币B 的期望为0.004/(0.004+0.001)=0.20 9H1T0.80*9H1T + 0.20*9H1T 7.2H,0.8T + 1.8H,0.2T 𝜃መ 𝐴 = 7.2 7.2+0.8 , 𝜃መ 𝐵 = 1.8 1.8+0.2 如果是A硬币,抛出 HHHHTHHHHH的概率是𝜃 𝐴 9 (1- 𝜃 𝐴 ) 1=0.69×0.41=0.010077696×0.4 ≈ 0.004 如果是B硬币,抛出 HHHHTHHHHH的概率是𝜃 𝐵 9 (1- 𝜃 𝐵 ) 1=0.510≈ 0.001 C. B. Do and S. Batzoglou, "What is the expectation maximization algorithm?," Nature Biotechnology, vol. 26, p. 897, 08/01/online 2008
信息检索与数据挖掘 2019/5/514 EM算法示例:求两个硬币随机抛出后正反面的概率 迭代过程分析 x=(x,x2,,x),x,∈{0,1,,10}第i次抛硬币试验中正面(head)朝上的次数 2=(31,22,,5),,∈{4,B}第i次抛硬币试验 ②求隐变量Z的后验概率 X和Z的联合概率 X=(K1=5,x2=9,x3=8,x4=4,X=7) P(z1=Ax;00) Z是隐变量 P(x,Z1=Ax1;0) P(21=B1x:00) E-step P(xz=B:) Coin A Coin B THHTHTH: 0.45 A =2.2H,2.2T ≈2.8H,2.8T 0.80 0.20 ≈72H,0.8T ≈1.8H,0.2T HTTTHHTT HHHTHHHTH 0.73 0.21 =5.9H,1.5T ≈2.1H,0.5T 0.35 0.65x 1.4H,2.1T ③从联合概率求边缘概率 6=0.60 0.65 ≈4.5H.1.9T 在88■gg中 6=0.50 ≈21.3H,8.6T a=Pa=Ax:00 g00ngg▣ggg▣0gge0g00ege 21.3 =P(z:=Bx:0) 21.3+8.6=0.71 M-step 11.7+8.4≈0.58 6o=0.80 60=0.52 C.B.Do and S.Batzoglou,"What is the expectation maximization algorithm?,"Nature Biotechnology,vol.26,p.897,08/01/online 2008
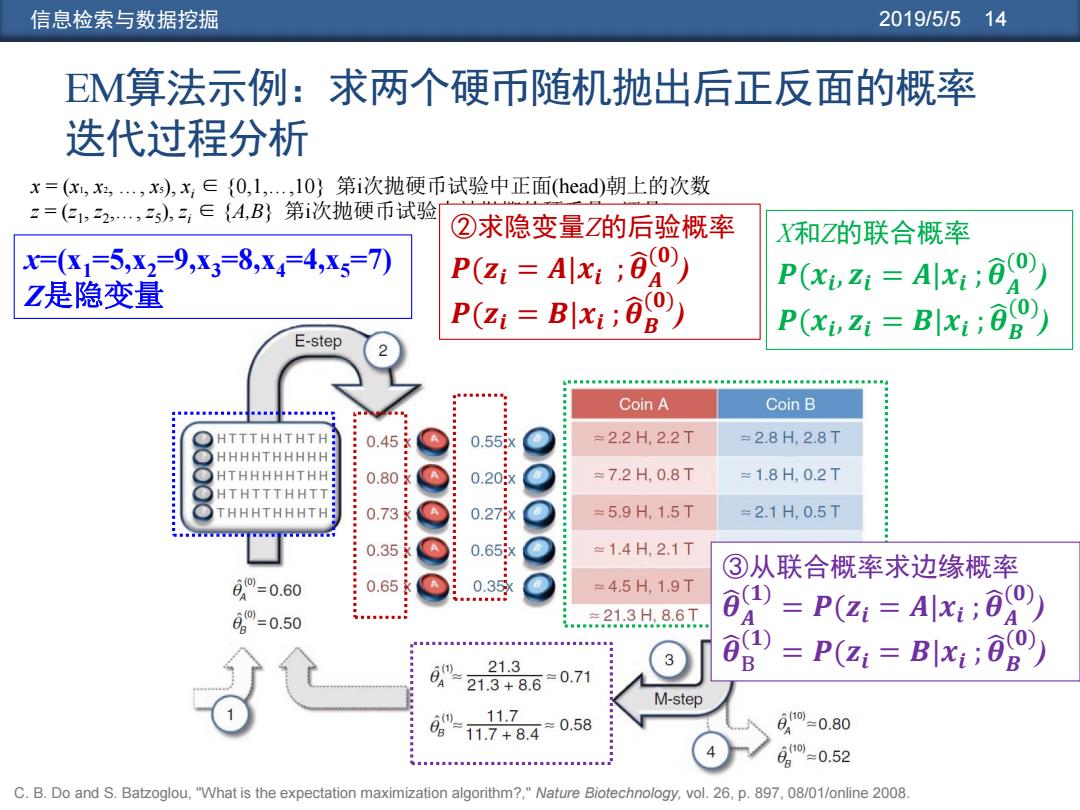
信息检索与数据挖掘 2019/5/5 14 EM算法示例:求两个硬币随机抛出后正反面的概率 迭代过程分析 x = (x1, x2, …, x5), xi ∈ {0,1,…,10} 第i次抛硬币试验中正面(head)朝上的次数 z = (z1 , z2 ,…, z5 ), zi ∈ {A,B} 第i次抛硬币试验中被抛掷的硬币是A还是B ②求隐变量Z的后验概率 𝑷(𝒛𝒊 = 𝑨|𝒙𝒊 ; 𝜽 𝑨 (𝟎) ) 𝑷(𝒛𝒊 = 𝑩|𝒙𝒊 ; 𝜽 𝑩 (𝟎) ) X和Z的联合概率 𝑷(𝒙𝒊 , 𝒛𝒊 = 𝑨|𝒙𝒊 ; 𝜽 𝑨 (𝟎) ) 𝑷(𝒙𝒊 , 𝒛𝒊 = 𝑩|𝒙𝒊 ;𝜽 𝑩 (𝟎) ) x=(x1=5,x2=9,x3=8,x4=4,x5=7) Z是隐变量 ③从联合概率求边缘概率 𝜽 𝑨 (𝟏) = 𝑷(𝒛𝒊 = 𝑨|𝒙𝒊 ; 𝜽 𝑨 (𝟎) ) 𝜽 B (𝟏) = 𝑷(𝒛𝒊 = 𝑩|𝒙𝒊 ;𝜽 𝑩 (𝟎) ) C. B. Do and S. Batzoglou, "What is the expectation maximization algorithm?," Nature Biotechnology, vol. 26, p. 897, 08/01/online 2008
信息检索与数据挖掘 2019/5/515 EM算法: 01t-2) 迭代过程不断构造更好的下 log P(x;0) 先固定当前参数,计算得到当前隐变 量分布的一个下界(Lower Bound)函 数,然后优化这个函数,得到新的 参数,然后循环继续。 g: p(X;)=∑zp(X,Z;)-从联合概率计算边缘概率 pX;9)=∑q2 px2:0) ←- q(Z) q(Z)=p(ZX;0), 构造的先验分布 p(X,Z;8) -Jensen's inequality q (Z o÷∑4t☒iog2”29-∑pax6s p(X,Z;0) p(zx;0t) 0t+1)=argmax gt(0)←gt(0)是logp(X;0)的1 ower bound C.B.Do and S.Batzoglou,"What is the expectation maximization algorithm?,"Nature Biotechnology,vol.26,p.897,08/01/online 2008. 关于EM算法的九层境界的浅薄介绍htp:wwmw.elecfans.comd/604076.html
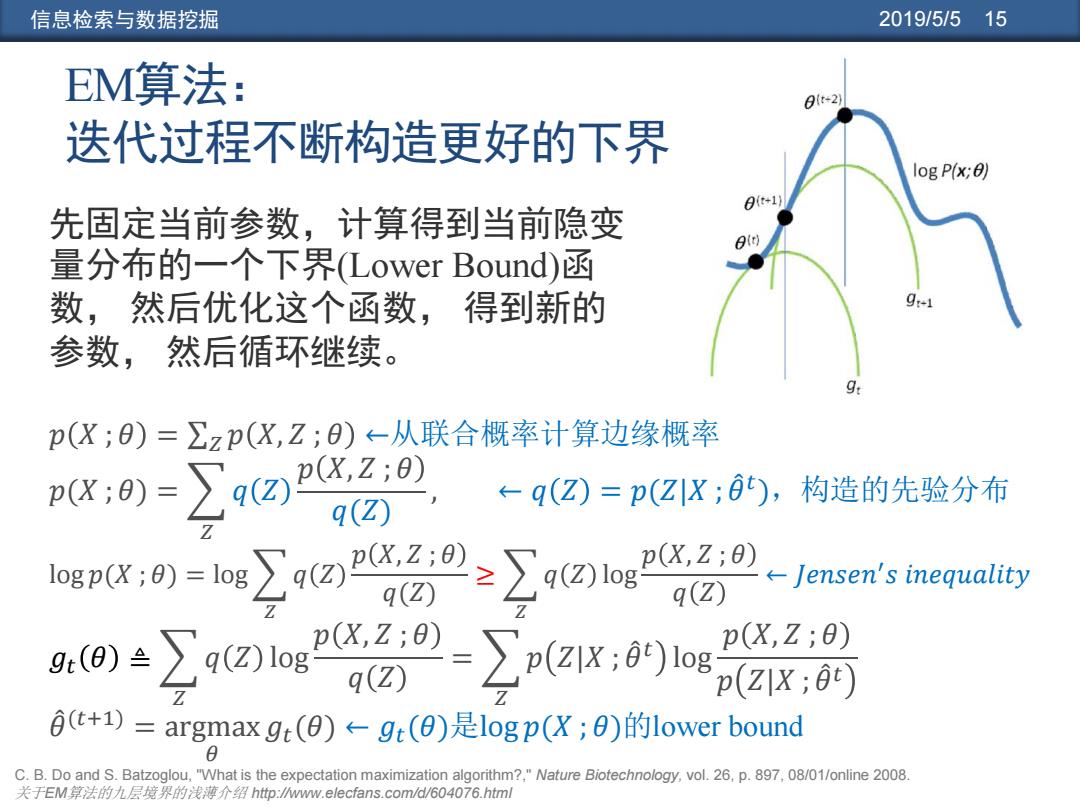
信息检索与数据挖掘 2019/5/5 15 𝑝 𝑋 ; 𝜃 = σ𝑍 𝑝 𝑋, 𝑍 ; 𝜃 ←从联合概率计算边缘概率 𝑝(𝑋 ; 𝜃) = 𝑍 𝑞 𝑍 𝑝 𝑋, 𝑍 ; 𝜃 𝑞(𝑍) , ← 𝑞 𝑍 = 𝑝(𝑍|𝑋 ; 𝜃መ 𝑡 ),构造的先验分布 log 𝑝(𝑋 ; 𝜃) = log 𝑍 𝑞 𝑍 𝑝 𝑋, 𝑍 ; 𝜃 𝑞(𝑍) ≥ 𝑍 𝑞 𝑍 log 𝑝 𝑋, 𝑍 ; 𝜃 𝑞 𝑍 ← 𝐽𝑒𝑛𝑠𝑒𝑛 ′ 𝑠 𝑖𝑛𝑒𝑞𝑢𝑎𝑙𝑖𝑡𝑦 𝑔𝑡 𝜃 ≜ 𝑍 𝑞 𝑍 log 𝑝 𝑋, 𝑍 ; 𝜃 𝑞 𝑍 = 𝑍 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 log 𝑝 𝑋, 𝑍 ; 𝜃 𝑝 𝑍|𝑋 ; 𝜃መ 𝑡 𝜃መ (𝑡+1) = argmax 𝜃 𝑔𝑡(𝜃) ← 𝑔𝑡(𝜃)是log 𝑝(𝑋 ; 𝜃)的lower bound EM算法: 迭代过程不断构造更好的下界 先固定当前参数,计算得到当前隐变 量分布的一个下界(Lower Bound)函 数, 然后优化这个函数, 得到新的 参数, 然后循环继续。 C. B. Do and S. Batzoglou, "What is the expectation maximization algorithm?," Nature Biotechnology, vol. 26, p. 897, 08/01/online 2008. 关于EM算法的九层境界的浅薄介绍 http://www.elecfans.com/d/604076.html