
信息检索与数据挖掘 2019年4月16日 信息检索与数据挖掘 第10章文本分类 part1:文本分类及朴素贝叶斯方法 part2:基于向量空间的文本分类 part3:支持向量机及机器学习方法
信息检索与数据挖掘 2019年4月16日 信息检索与数据挖掘 第10章 文本分类 part1: 文本分类及朴素贝叶斯方法 part2: 基于向量空间的文本分类 part3: 支持向量机及机器学习方法

信息检索与数据挖掘 2019年4月16日 讨论3-3-1:分类器(分类函数) ·学习方法不同,得到的分类函数Y不同 ·若学习方法固定,训练集D不同,Y是否相同? (d)=arg max P(c)II P(Xx=tlc) cEC 1<k<nd Cmap arg max P(cld)=arg max P(c)P(tklc) ceC ceC 1≤k≤na P(c)-N P(1c)= ·训练集D改变则P(c)和Ptc改变→Y改变 对于某固定学习方法,训练集改变使分类函数变化,不同的分类函数产生的 决策结果如果基本一致,我们说该学习方法的方差不大,如果不同分类函数 的决策结果差异性很大,我们说该学习方法的方差大
信息检索与数据挖掘 2019年4月16日 讨论3-3-1:分类器(分类函数) • 学习方法不同,得到的分类函数 不同 • 若学习方法固定,训练集 不同, 是否相同? • 训练集 改变则^P(c)和^P(tk |c)改变 改变 对于某固定学习方法,训练集改变使分类函数变化,不同的分类函数产生的 决策结果如果基本一致,我们说该学习方法的方差不大,如果不同分类函数 的决策结果差异性很大,我们说该学习方法的方差大 2

信息检索与数据挖掘 2019年4月16日 讨论3-3-2:分类器(分类函数)的误差 ·实际情沉是P(cd 。学习后分类器输出P(Cd) ·P(cd)与P(cldW之间的差异就是误差 14.6章节,p216 ·误差常用MSE衡量,MSE:ELP(C-P(CI2 E[x-a2=Ex2-2Exa +a2=Ex-ap2+E[x-Ex 2 ·令x=P(c记为P=P(cW记为P .EIAP-P2=EAP-PP+EAP-EAP2 偏差bias、方差variance 3
信息检索与数据挖掘 2019年4月16日 讨论3-3-2:分类器(分类函数)的误差 • 实际情况是 P(c|d) • 学习后分类器输出 ^P(c|d) • ^P(c|d) 与 P(c|d) 之间的差异就是误差 • 误差常用MSE衡量,MSE:Ed [^P(c|d) - P(c|d) ] 2 • E[x- α] 2 = Ex2 − 2Exα +α2 = [Ex − α] 2 + E[x − Ex ] 2 • 令x= ^P(c|d) 记为^P, α= P(c|d) 记为P • E[^P- P] 2 = [E^P − P]2 + E[^P − E^P ] 2 • 偏差 bias、方差 variance 14.6章节,p216 3
信息检索与数据挖掘 2019年4月16日 讨论3-3-3:偏差一方差折中准则 学习误差=偏差+方差。通常情况下,这两个部 分不会同时最小。当我们比较两个学习方法T和T2 时,大部分情况下最后的结果都是,其中一个方法 偏差高方差低而另一个方法偏差低方差高。因此, 从两个学习方法中选择一个时,我们不是简单地选 择能够在不同训练集上产生好的分类器的学习方法 (方差小),也不是选择那些能学出复杂决策边界 的学习方法(偏差小)。实际的做法是,根据应用 的需要,选择不同的权重对偏差和方差进行加权求 和。这种折衷称为偏差-方差折衷准则(bias variance tradeoff)
信息检索与数据挖掘 2019年4月16日 讨论3-3-3:偏差—方差折中准则 • 学习误差 = 偏差 + 方差。通常情况下,这两个部 分不会同时最小。当我们比较两个学习方法Г1和Г2 时,大部分情况下最后的结果都是,其中一个方法 偏差高方差低而另一个方法偏差低方差高。因此, 从两个学习方法中选择一个时,我们不是简单地选 择能够在不同训练集上产生好的分类器的学习方法 (方差小),也不是选择那些能学出复杂决策边界 的学习方法(偏差小)。实际的做法是,根据应用 的需要,选择不同的权重对偏差和方差进行加权求 和。这种折衷称为偏差-方差折衷准则(bias– variance tradeoff)。 4
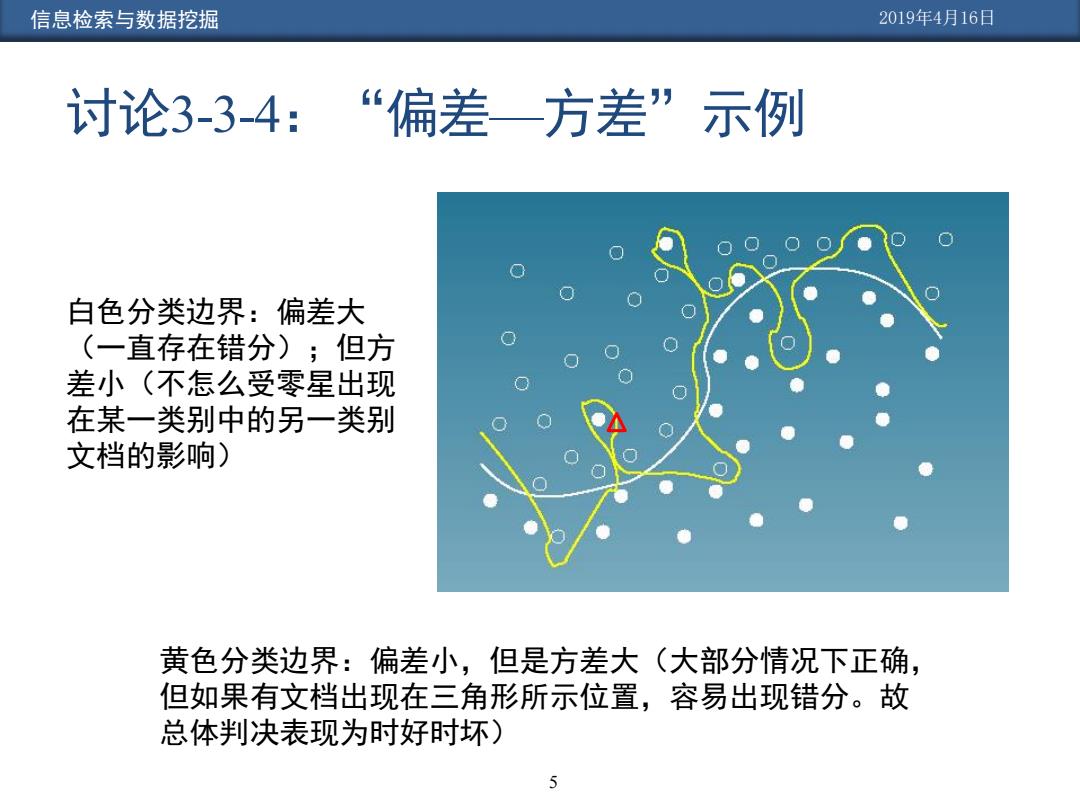
信息检索与数据挖掘 2019年4月16日 讨论3-34: “偏差一方差”示例 白色分类边界:偏差大 (一直存在错分);但方 差小(不怎么受零星出现 在某一类别中的另一类别 文档的影响) 黄色分类边界:偏差小,但是方差大(大部分情况下正确, 但如果有文档出现在三角形所示位置,容易出现错分。故 总体判决表现为时好时坏) 5
信息检索与数据挖掘 2019年4月16日 讨论3-3-4:“偏差—方差”示例 黄色分类边界:偏差小,但是方差大(大部分情况下正确, 但如果有文档出现在三角形所示位置,容易出现错分。故 总体判决表现为时好时坏) 白色分类边界:偏差大 (一直存在错分);但方 差小(不怎么受零星出现 在某一类别中的另一类别 文档的影响) 5