
Mpx(T) 1700K 1500K 1300K 1100K 2000 3000 2(A •斯特藩一 玻耳兹曼定律 Ma(T)=Mn(T)da 曲线与横轴围的面积 σ=5.67×10-8Wm2.K4 Ma(T)=oT 斯特藩常量 西的肉例
------------------------------------------------------------------------------- (Å) MB (T) 2000 3000 •斯特藩 — 玻耳兹曼定律 MB (T) MB (T)d 0 = 曲线与横轴围的面积 4 MB (T) = T = 5.67×10-8 W·m-2·K-4 斯特藩 常量

·维恩位移定律 MBR(T) 2 九m 峰值波长 AT=b b=2.897×10-3m:K,维恩常量 当绝对黑体的温度升高时,单色辐射出射度最 大值向短波方向移动。 的内网
------------------------------------------------------------------------------- • 维恩位移定律 峰值波长 m T = b M (T ) B m b=2.897×10-3 m·K,维恩常量 当绝对黑体的温度升高时,单色辐射出射度最 大值向短波方向移动

二、普朗克量子假役和普朗克公式 1900年,普朗克从理论上推导出一个与实验符合 得非常好的公式 MB2(T)=2hc22-5 euT-1 c一光速,k—玻尔兹曼恒量 为推导出这个公式,普朗克作了如下两条假设 (1)黑体是由带电谐振子组成,这些谐振子辐射电磁波, 并和周围的电磁场交换能量。 (2)这些谐振子能量不能连续变化,只能取一些分立值 是最小能量ε的整数倍,这个最小能量称为能量子。 8,28,38,, n8, ghy.称为能量子
------------------------------------------------------------------------------- 二、普朗克量子假设和普朗克公式 1900年,普朗克从理论上推导出一个与实验符合 得非常好的公式 1 1 2 2 5 − = − k T B hc e M (T ) hc c —光速, k —玻尔兹曼恒量 为推导出这个公式,普朗克作了如下两条假设 (1)黑体是由带电谐振子组成,这些谐振子辐射电磁波, 并和周围的电磁场交换能量。 (2) 这些谐振子能量不能连续变化,只能取一些分立值 ,是最小能量 的整数倍,这个最小能量称为能量子。 ,2 ,3 ,…,n ,… =hv 称为能量子

h=6.6260755×10-34Js普朗克常数 普朗克公式的得出,是理论和实验结合的典范。 •打破“一切自然过程能量都是连续的”经典看法 ·敲开量子力学的大门 普朗克获得1918年诺贝尔物理学奖 商的内网
------------------------------------------------------------------------------- h = 6.6260755×10-34 J·s 普朗克常数 •普朗克公式的得出,是理论和实验结合的典范。 •打破“一切自然过程能量都是连续的”经典看法 •敲开量子力学的大门 普朗克获得1918年诺贝尔物理学奖
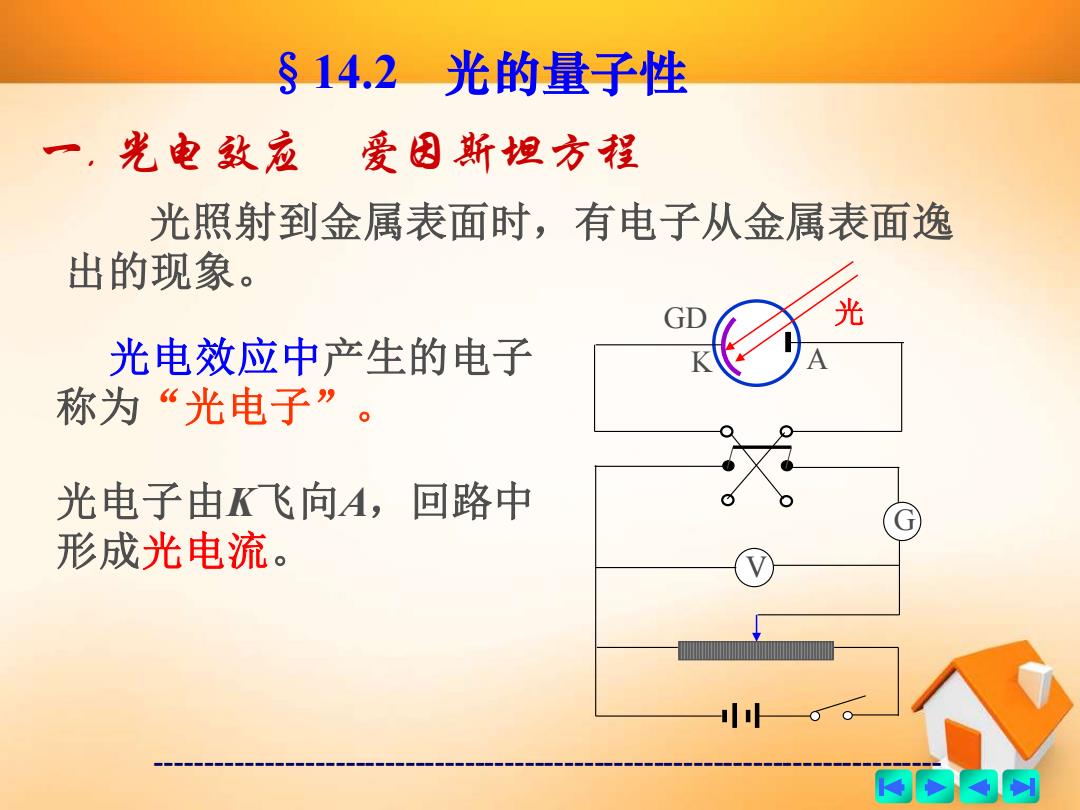
§14.2光的量子性 一,光电致在 爱因斯坦方程 光照射到金属表面时,有电子从金属表面逸 出的现象。 光 光电效应中产生的电子 称为“光电子”。 光电子由K飞向A,回路中 形成光电流。 两的肉例
------------------------------------------------------------------------------- §14.2 光的量子性 一. 光电效应 爱因斯坦方程 光照射到金属表面时,有电子从金属表面逸 出的现象。 G V GD K A 光 光电效应中产生的电子 称为“光电子”。 光电子由K飞向A,回路中 形成光电流