
2、码的唯一可译性 (1)基本概念 奇异码:一组码中含相同码字 非奇异码:所有的码字都不相同 唯一可译性:码字组成的任意有限长码字序 列都能恢复成唯一的信源序列 续长码:有些码字是在另一些码字后 面添加码元得来的 及时码:码字的最后一个码元出现时,译码 器能立即判断一个码字已经结束,可以立 即译码 非续长码:任一码字都不是其它码字的延长。 第四章离散无记忆信源 信息理论与编码 6 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 6 2、码的唯一可译性 (1)基本概念 奇异码:一组码中含相同码字。 非奇异码:所有的码字都不相同。 唯一可译性:码字组成的任意有限长码字序 列都能恢复成唯一的信源序列。 续长码:有些码字是在另一些码字后 面添加码元得来的。 及时码:码字的最后一个码元出现时,译码 器能立即判断一个码字已经结束,可以立 即译码。 非续长码:任一码字都不是其它码字的延长
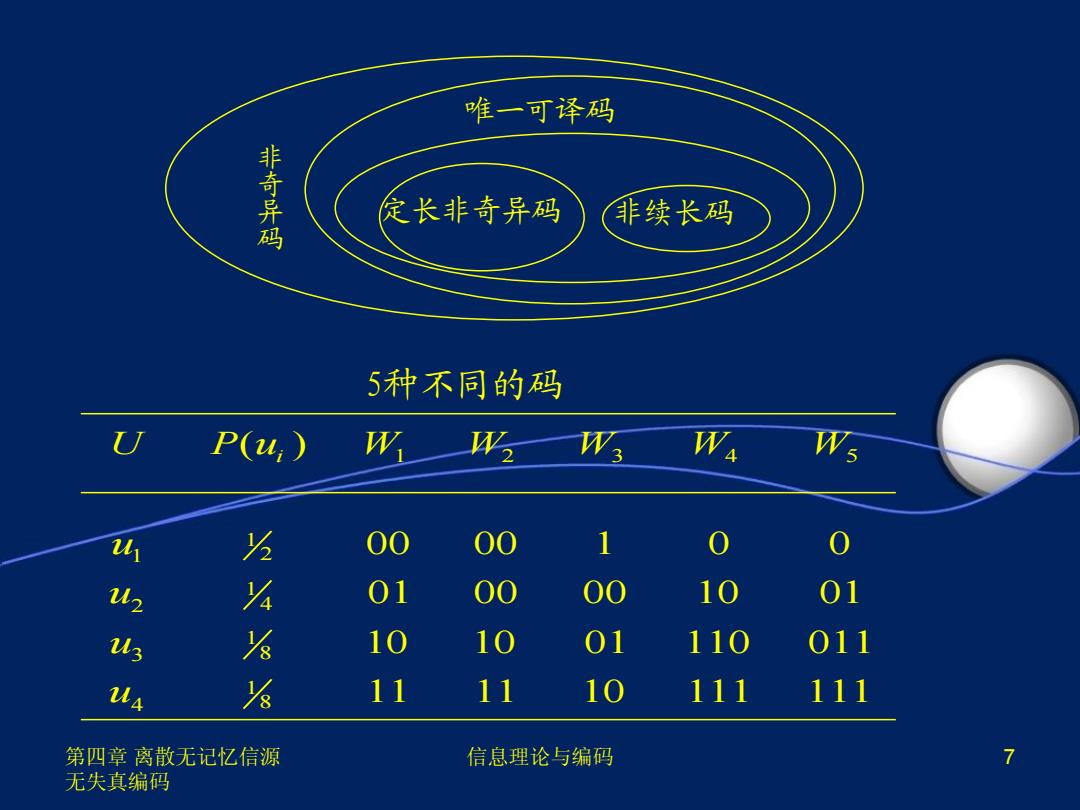
唯一可译码 非奇异码 定长非奇异码 非续长码 5种不同的码 U P(4,) W W2 W3 Wa Ws 为 00 00 1 0 % 01 00 00 10 01 u3 ⅓ 10 10 01 110 011 Us 名 11 11 10 111 111 第四章离散无记忆信源 信息理论与编码 7 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 7 唯一可译码 定长非奇异码 非续长码 非 奇 异 码 5种不同的码 1 2 4 3 5 1 1 2 1 2 4 1 3 8 1 4 8 ( ) 00 00 1 0 0 01 00 00 10 01 10 10 01 110 011 11 11 10 111 111 U P u W W i W W W u u u u

(2)码树和Kraft不等式 从树根开始,生长r个树枝,在节点处 再各自生长r个树枝。 节点:树枝与树枝的交点。 1阶节,点:经过1根树枝到达的节,点。 整树:节点长出的树枝数等于工 定理:对于任一ǐ进制非续长码,各码 字的码长必须满足Kraft不等式:∑r≤1 反过来,若上式成立,就一定能构造一个ǐ 进制非续长码。 第四章离散无记忆信源 信息理论与编码 8 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 8 (2)码树和Kraft不等式 从树根开始,生长r个树枝,在节点处 再各自生长r个树枝。 节点:树枝与树枝的交点。 l阶节点:经过l根树枝到达的节点。 整树:节点长出的树枝数等于r 定理:对于任一r进制非续长码,各码 字的码长必须满足Kraft不等式: 反过来,若上式成立,就一定能构造一个r 进制非续长码。 1 1 i q l i r

定理 对于任一进制唯一可译码 (UDC),各码字的码长必须满足Kraft不 等式: 之x4 ≤1 反过来,若上式成立,就一定能构造 一个进制唯一可译码(UDC) 第四章离散无记忆信源 信息理论与编码 9 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 9 定理 对于任一进制唯一可译码 (UDC),各码字的码长必须满足Kraft不 等式: 反过来,若上式成立,就一定能构造 一个进制唯一可译码(UDC)。 1 i 1 q l i r