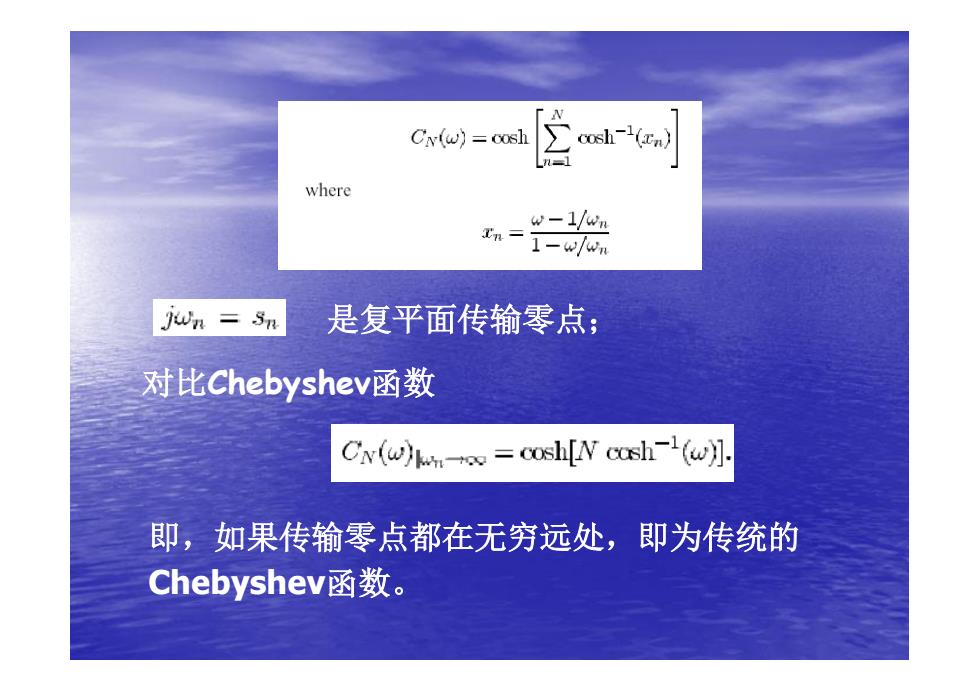
Cx(w) cosh cosh-1(arn) where w-1/wn n= 1-w/Wn jwn Sn 是复平面传输零点; 对比Chebyshevi函数 Cw()=cosh[N cosh(w)] 即,如果传输零点都在无穷远处,即为传统的 Chebyshev函数
对比Chebyshev函数 是复平面传输零点; 即,如果传输零点都在无穷远处,即为传统的 Chebyshev函数

传输零点的位置关于虚轴对称,以保证滤波函数 C的分子和分母多项式的系数为纯实数。 FN() 1(w)= Fw(w) S21w)= PN(w) CN(w)= Pv(w】 EN(w) EEN(w) 有限传输零点的个数小于等于N-2),其他零点都 在无穷远。(谐振腔交叉耦合滤波器实现) Sa-2Vder'den 1 -[4
• 传输零点的位置关于虚轴对称,以保证滤波函数 CN 的分子和分母多项式的系数为纯实数。 • 有限传输零点的个数小于等于(N-2),其他零点都 在无穷远。(谐振腔交叉耦合滤波器实现)

I.2 General Chebyshev"有理分式求解 与Chebyshevi函数类似,现在求解General Chebyshev函数的有理分式表示。 首先进行cos1的恒等变换: N CN(w)=cosh ln(an+bn) Ln=1 其中, an In b=(哈-11/2
1.2 General Chebyshev有理分式求解 与Chebyshev函数类似,现在求解General Chebyshev函数的有理分式表示。 首先进行cos-1的恒等变换: 其中
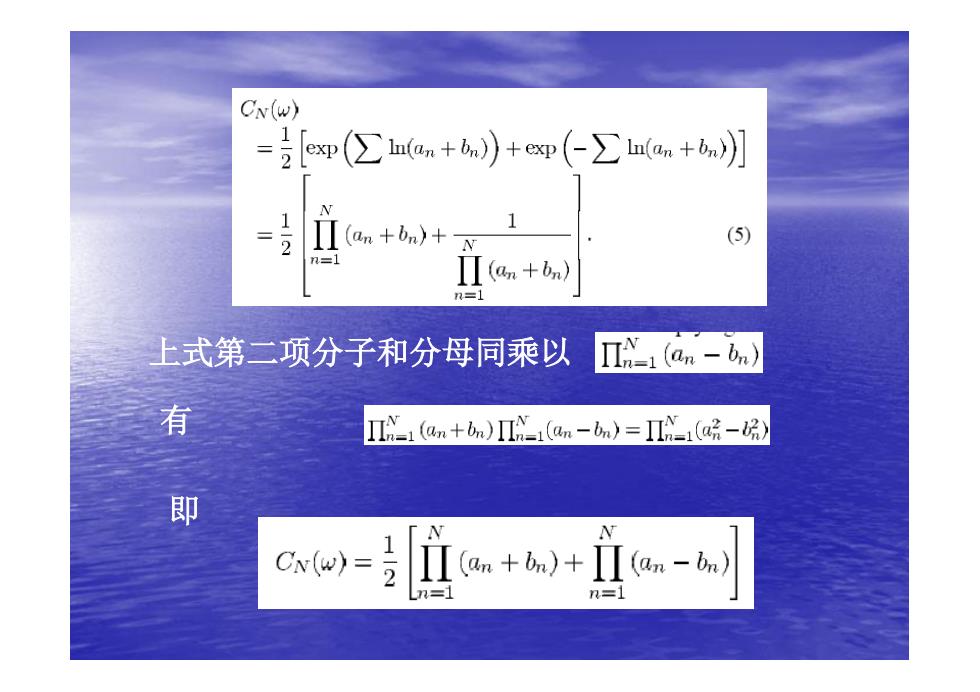
CN(w) m(∑nas+)+m(-∑haa+b】 = (5) am+bn) =1 上式第二项分子和分母同乘以 Π1(an-bn) 有 I1an+bn)I1(an-bn)=Ⅱ旷1(a品-)》 即 CN(w)= 12 Le+a+立a-a刻 =1
上式第二项分子和分母同乘以 有 即

带入整理得到: +d)+Πo-d) CN(W)= 1-2 n=1 =1 0-“) =1 其中, 1 Cn=W- Wn 1)/2 4=(1- w'=(w2-1)1/2
带入整理得到: 其中