
例6-1外伸梁受力如图a所示。梁由钢板焊接而成,截面尺寸如图d所示。已知[口]=120 MPa,[d=60MPa,试校核梁的强度,并求焊缝ab处的剪应力。 90KN 20KN/m (a) R 40KN 25K d 65K 25KNm (c) (e) (0 40KN. 例图6-1 解:(1)求支座反力并画内力图 由平衡条件求得R,=25kN,Ra=105kN 梁的剪力图和弯矩图分别如图b、c所示。 M=40kN·m,发生在B截面处 lg=65kN,发生在B左截面处。 (2)计算截面的几何性质 图d中y为对称轴。选择参考坐标轴三,确定形心C的位置。 =100x20x10+2x200x20x10-82mm 100×20+2×200×20 通过形心C的y、:轴为形心主轴,z为中性轴。求形心主轴惯性矩I。 1.=(2×100×20'+100×20×72) +2×(2×20×2003+200×20x18*)=3.97x10'(mm) (3)强度校核 沿B截面的高度正应力分布如图©所示,最大正应力发生在截面的下边缘处, g==M=y==40x10x1I8=1189MPa<O]-120MPa 3.97×107 正应力满足强度要求: 沿B:截面的高度剪应力分布如图f所示,最大剪应力发生在中性轴处
例 6-1 外伸梁受力如图a所示。梁由钢板焊接而成,截面尺寸如图d所示。已知 =120 NPa, = 60 NPa,试校核梁的强度,并求焊缝 ab 处的剪应力。 解:(1)求支座反力并画内力图 由平衡条件求得 RA = 25 kN, RB =105 kN 梁的剪力图和弯矩图分别如图 b、c 所示。 40 max M = kN·m,发生在 B 截面处。 65 max Q = kN,发生在 B 左截面处。 (2)计算截面的几何性质 图 d 中 y 为对称轴。选择参考坐标轴 1 z ,确定形心 C 的位置。 82 100 20 2 200 20 100 20 10 2 200 20 100 = + + zC = (mm) 通过形心 C 的 y 、 z 轴为形心主轴, z 为中性轴。求形心主轴惯性矩 z I 。 20 200 200 20 18 ) 3.97 10 (mm ) 12 1 2 ( 100 20 100 20 72 ) 12 1 ( 3 2 7 4 3 2 + + = I z = + (3)强度校核 沿 B 截面的高度正应力分布如图 e 所示,最大正应力发生在截面的下边缘处, 118.9 3.97 10 40 10 118 7 6 max max max = = = z I M y NPa< =120 NPa 正应力满足强度要求; 沿 B 左截面的高度剪应力分布如图 f 所示,最大剪应力发生在中性轴处

(S:)m=2×20x118×)×118=2.75×103(mm) 2m(S)_65×103x2.75×10 =11.4 MPa<[r]=60 MPa bl, 2×20×3.97×107 剪应力亦满足强度要求。该梁安全。 通过本例可以看出,梁的强度计算主要是满足正应力的强度条件,一般不用校核t。 (4)焊缝b处的剪应力 在焊缝b处将截面截为两部分,求出其中任一部分(例如左部分)对中性轴:的静 S=200×20×18=7.2×103(mm3) Tas =as =65×10×72×10: =5.9 MPa bl. 20×397×10 本题要点 1.明确分析弯曲强度问题的计算步骤:外力一内力一危险面(M、)一 一危险面上的应力分布—一危险点的应力及其应力状态—强度条件。 2.熟悉弯曲正应力及弯曲剪应力的计算公式。 例6-2一铸铁梁的受力如图a所示,其截面尺寸如图b所示。铸铁材料的拉、压许用应力 分别为[o,]=40MPa及[o]=80MPa。试校核此梁是否安全。 解:(1)绘梁的内力 c12 梁的马矩图如c所示。 (2)计算截面的几何 性质 用与例6-1相同的方 法,求得形心C距上、下 边缘的距离分别为52mm 和88mm,形心主惯性矩 L.=7.64×106mm4。 d (3)强度校核 本例中因剪力在梁中 C藏面 B裁面 引起的剪应力较小,故只 例图6-2 对正应力进行校核。由于 梁的截面上、下不对称于中性轴,而材料的拉、压许用应力又不相等,所以最大正弯矩的作用 截面C和最大负弯矩的作用截面B均可能是危险面。两个截面上的正应力分布如图所示。可 以看出,最大压应力发生在B截面下边缘的各点处,其值为
5 max * 118 2.75 10 2 1 (Sz ) = 2 20118 = (mm3) 11.4 2 20 3.97 10 ( ) 65 10 2.75 10 7 3 5 max * max max = = = y y bI Q S NPa< =60 NPa 剪应力亦满足强度要求。该梁安全。 通过本例可以看出,梁的强度计算主要是满足正应力的强度条件,一般不用校核 max 。 (4)焊缝 ab 处的剪应力 在焊缝 ab 处将截面截为两部分,求出其中任一部分(例如左部分)对中性轴 z 的静 矩: * 4 Sz = 200 2018 = 7.210 (mm3) 5.9 20 3.97 10 65 10 7.2 10 7 * 3 4 = = = z z ab bI QS NPa 本题要点 1.明确分析弯曲强度问题的计算步骤:外力——内力——危险面( M max 、 max Q )— —危险面上的应力分布——危险点的应力及其应力状态——强度条件。 2.熟悉弯曲正应力及弯曲剪应力的计算公式。 例 6-2 一铸铁梁的受力如图 a 所示,其截面尺寸如图 b 所示。铸铁材料的拉、压许用应力 分别为 [ ] = 40MPa + 及 [ ] = 80MPa − 。试校核此梁是否安全。 解:(1)绘梁的内力 图 梁的弯矩图如c所示。 (2)计算截面的几何 性质 用与例 6-1 相同的方 法,求得形心 C 距上、下 边缘的距离分别为 52mm 和 88mm,形心主惯性矩 6 4 I z = 7.6410 mm 。 (3)强度校核 本例中因剪力在梁中 引起的剪应力较小,故只 对正应力进行校核。由于 梁的截面上、下不对称于中性轴,而材料的拉、压许用应力又不相等,所以最大正弯矩的作用 截面 C 和最大负弯矩的作用截面 B 均可能是危险面。两个截面上的正应力分布如图 d 所示。可 以看出,最大压应力发生在 B 截面下边缘的各点处,其值为

g=M2==5x10×88 57.6MPa<[o.] Iy 7.64×109 最大拉应力发生在C截面下边缘的各点处,其值为 g=4,-35X0X88-403Mm<o,K105=42Mma 7.64×109 [o]虽然大于[σ,],但没超过5%,故仍然认为是安全的。 试问若将梁倒着放置时,此梁是否仍然安全? 根据本例的分析结果,读者不妨结算一下,对于横截面上、下不对称于中性轴的脆性材料 梁,进行强度计算时应注意什么问题。 本题要点 1.弯曲强度计算的步聚。 2.对于拉、压强度不等的梁,必须分别校核最大拉应力和最大压应力。 例6-3简支梁在跨中受集中载荷P=30kN,1=8m,[o]=120MPa (1)试为梁选择工字钢型号。 (2)当P提高为40k时,原工字钢型号不变,试问采取什么措施使梁仍能满足强度条 件。 80X10 122 c (a) (b) 例图6-3 解:(1)选择工字钢型号 图6-3a简支梁的M发生在跨中 Mm=-x0x8=60N.m) 4 根据强度条件式(6-7) =60xl0-5x10(am w.zol 120 选择工字钢恤28a W.=508cm3,L.=7.11×103cm (2)当P=40kN时,提高梁承载能力的措施
57.6MPa [ ] 7.64 10 5 10 88 6 6 max max − − = = = y B I M z 最大拉应力发生在 C 截面下边缘的各点处,其值为 40.3MPa [ ] 1.05 42 MPa 7.64 10 3.5 10 88 6 6 max max = = = = + + y C I M z [ ] max + 虽然大于 [ ] + ,但没超过 5%,故仍然认为是安全的。 试问若将梁倒着放置时,此梁是否仍然安全? 根据本例的分析结果,读者不妨结算一下,对于横截面上、下不对称于中性轴的脆性材料 梁,进行强度计算时应注意什么问题。 本题要点 1.弯曲强度计算的步骤。 2.对于拉、压强度不等的梁,必须分别校核最大拉应力和最大压应力。 例 6-3 简支梁在跨中受集中载荷 P = 30 kN,l = 8 m,[ ] = 120 NPa。 (1)试为梁选择工字钢型号。 (2)当 P 提高为 40kN 时,原工字钢型号不变,试问采取什么措施使梁仍能满足强度条 件。 解:(1)选择工字钢型号 图 6-3a 简支梁的 Mmax 发生在跨中 30 8 60 4 1 4 max = l = = P M (kN·m) 根据强度条件式(6-7) 5 6 max 5 10 120 60 10 [ ] = = M Wz (mm3) 选择工字钢№28a Wz = 508 cm3, 3 I z = 7.1110 cm4 (2)当 P = 40 kN 时,提高梁承载能力的措施

方法一:在原梁上增加一长度为a的副梁CD,将P作用在副梁上,如图63b所示。使 M。=M面M:-学.M=那a a=4.95m≈5.0m 根据式(67),副梁的截面应为 40×5×10 4 120 -=4.17×103(mm3) 副梁CD工字钢的型号为25b,W.=423cm3。 方法二:在原梁上下艺缘各焊一长度为a,截面为80mm×10mm的钢板条,如图6-3c所 示。加焊钢板后截面对中性轴的惯性矩为 1.=711x102+2×(7×80x103+80x10x1452)=10.,47x102(mm 50x10115MPac]-120 MPa 10.47×107 焊钢板后的截面能满足梁的强度条件。 本题要点 1.梁的截面选择 2.提高梁承载能力的措施。具体采用那种措施,应视具体条件而定。若仅为一次性的载 荷加大,则采用方法一:若为永久性的加大吊车起重载荷,则采用方法二。 例6-4矩形截面梁由两种材料粘结在一起制成,受到弯矩M作用。设梁弯曲时平面假设 仍然成立。已知E,=4E,。(1)绘出横截面上正应力沿截面高度的分布图。(2)求当M=5 kN·m,h=2b=100mm时,截面上的最大拉应力和最大压应力. 4234MP4 92.0 a (e) (b) 例图6-4 解:()因平面假定仍然成立,故应变沿截面高度为线性分布,式6=二仍然成立。式 中P为中性层的曲率半径,y为截面上的点到中性轴的距离。因E,≠E2,但N=0,故中
方法一:在原梁上增加一长度为 a 的副梁 CD,将 P 作用在副梁上,如图 6-3b 所示。使 M [M ] C = ,而 ) 2 2 ( 2 P l a M C = − ,[ ] [] M =Wz 。 ) 10 5.08 10 120 2 2 8 2 40 6 5 − = a ( a = 4.95m 5.0m 根据式(6-7),副梁的截面应为 5 6 max 4.17 10 120 40 5 10 4 1 = = M Wz (mm3) 副梁 CD 工字钢的型号为№25b,Wz = 423 cm3。 方法二:在原梁上下艺缘各焊一长度为 a,截面为 80mm×10mm 的钢板条,如图 6-3c 所 示。加焊钢板后截面对中性轴的惯性矩为 7 3 2 7 80 10 80 10 145 ) 10.47 10 12 1 I z = 7.1110 + 2 ( + = (mm4) 115 10.47 10 80 10 150 7 6 max max max = = = z I M y NPa< =120 NPa 焊钢板后的截面能满足梁的强度条件。 本题要点 1.梁的截面选择 2.提高梁承载能力的措施。具体采用那种措施,应视具体条件而定。若仅为一次性的载 荷加大,则采用方法一;若为永久性的加大吊车起重载荷,则采用方法二。 例 6-4 矩形截面梁由两种材料粘结在一起制成,受到弯矩 M 作用。设梁弯曲时平面假设 仍然成立。已知 E1 = 4E2 。(1)绘出横截面上正应力沿截面高度的分布图。(2)求当 M = 5 kN·m, h = 2b =100 mm 时,截面上的最大拉应力和最大压应力。 解:(1)因平面假定仍然成立,故应变沿截面高度为线性分布,式 y = 仍然成立。式 中 为中性层的曲率半径, y 为截面上的点到中性轴的距离。因 E1 E2 ,但 N = 0 ,故中
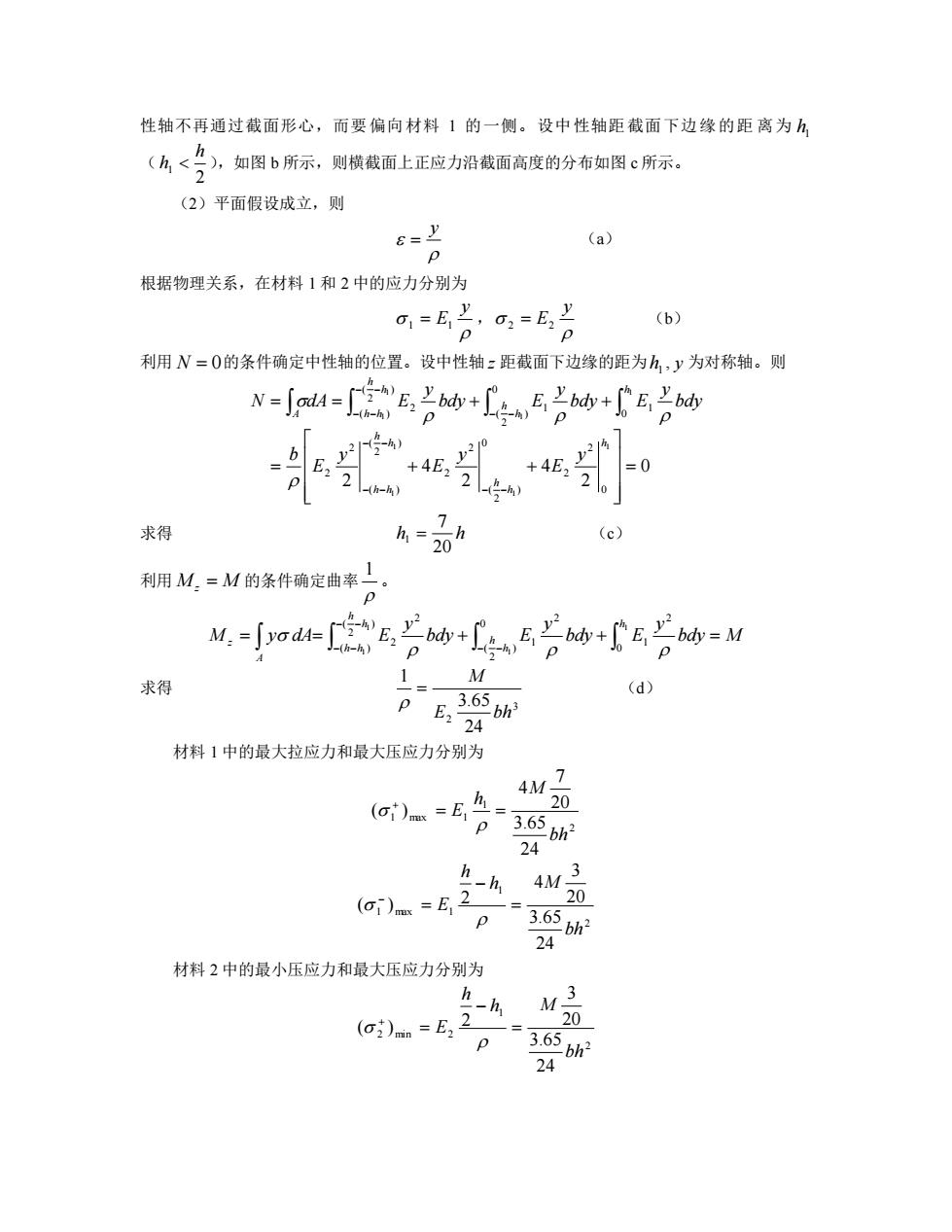
性轴不再通过截面形心,而要偏向材料1的一侧。设中性轴距截面下边缘的距离为, (九<号,如图6所示,则横酸面上正应力沿酸面高度的分布如图©所示。 (2)平面假设成立,则 6=y (a) 根据物理关系,在材料1和2中的应力分别为 a,=6片G=E (b) 利用N=0的条件确定中性轴的位置。设中性轴:距截面下边缘的距为h,y为对称轴。则 N-odld-E. +4E,2五,4, =0 2。 求得 (c) 利用M.=M的条件确定曲率 p M:-o信马若+马若+广a若=M 求得 M (d) 材料1中的最大拉应力和最大压应力分别为 (o)m=E4 20 p3.65 bh 24 (i)ms =E 2 20 24 材料2中的最小压应力和最大压应力分别为 p3656h 24
性轴不再通过截面形心,而要偏向材料 1 的一侧。设中性轴距截面下边缘的距 离为 1 h ( 2 1 h h ),如图 b 所示,则横截面上正应力沿截面高度的分布如图 c 所示。 (2)平面假设成立,则 y = (a) 根据物理关系,在材料 1 和 2 中的应力分别为 y 1 = E1 , y 2 = E2 (b) 利用 N = 0 的条件确定中性轴的位置。设中性轴 z 距截面下边缘的距为 1 h , y 为对称轴。则 0 2 4 2 4 2 1 1 1 1 1 1 1 1 0 2 2 0 ) 2 ( 2 2 ) 2 ( ( ) 2 2 0 1 0 ) 2 ( 1 ) 2 ( ( ) 2 = = + + = = + + − − − − − − − − − − − − h h h h h h h h h h h h A h h y E y E y E b bdy y bdy E y bdy E y N dA E 求得 h h 20 7 1 = (c) 利用 M z = M 的条件确定曲率 1 。 bdy M y bdy E y bdy E y M y dA E h h h h h h h A z = = + + = − − − − − − 1 1 1 1 0 2 1 0 ) 2 ( 2 1 ) 2 ( ( ) 2 2 求得 3 2 24 3.65 1 E bh M = (d) 材料 1 中的最大拉应力和最大压应力分别为 2 1 1 max 1 24 3.65 20 7 4 ( ) bh M h = E = + 2 1 1 max 1 24 3.65 20 3 4 2 ( ) bh h M h E = − = − 材料 2 中的最小压应力和最大压应力分别为 2 1 2 min 2 24 3.65 20 3 2 ( ) bh h M h E = − = +