例1-1设一杆沿轴线同时受力B,卫,乃的作用,其作用点分别为A、C、B,如图1-l 求杆的轴力。 P2-3kN2 P1=2kN P3=1kN (a) Pi=2kN P:-2kN P2-3N (b) 例图1-1 解:由于杆上有三个外力,因此在AC段和CB段的横截面上将有不同的轴力。 (1)在4C段内的任意处以横截面11将杆截为两段,取左段为研究对象,将右段对左段 的作用以内力N,代替(图1-1b)。由平衡条件知N,必与杆的轴线重合,方向与P相反,为拉 力,由平衡方程 ΣX=0,N1-P=0 N,=P =2kN 这就是AC段内任一横截面上的内力。 (2)再在CB段内的任意处以横截面2-2将杆截开,仍取左段为研究对象。此时因截面2 2上内力N2的方向一时不易确定,可将N2先设为拉力,如图1-lc所示,再由平衡方程 ΣX=0,N2-+=0 得 N,=P-E=2-3=-1kN 计算结果中的负号说明,该截面上内力的方向应与假设的方向相反,即八,为压力,其值为 IkN。此即CB段内任一横截面上的内力。 以上的计算,都是选取左段为研究对象,如果选取右段为研究对象,仍可得到同样的结果。 要点与讨论 直杆任一横截面上轴力,等于截面任意一侧杆段所受轴向外力的代数和。 例21试求图21中所示各杆在截面1-1、2-2、3-3上的轴力,并作轴力图
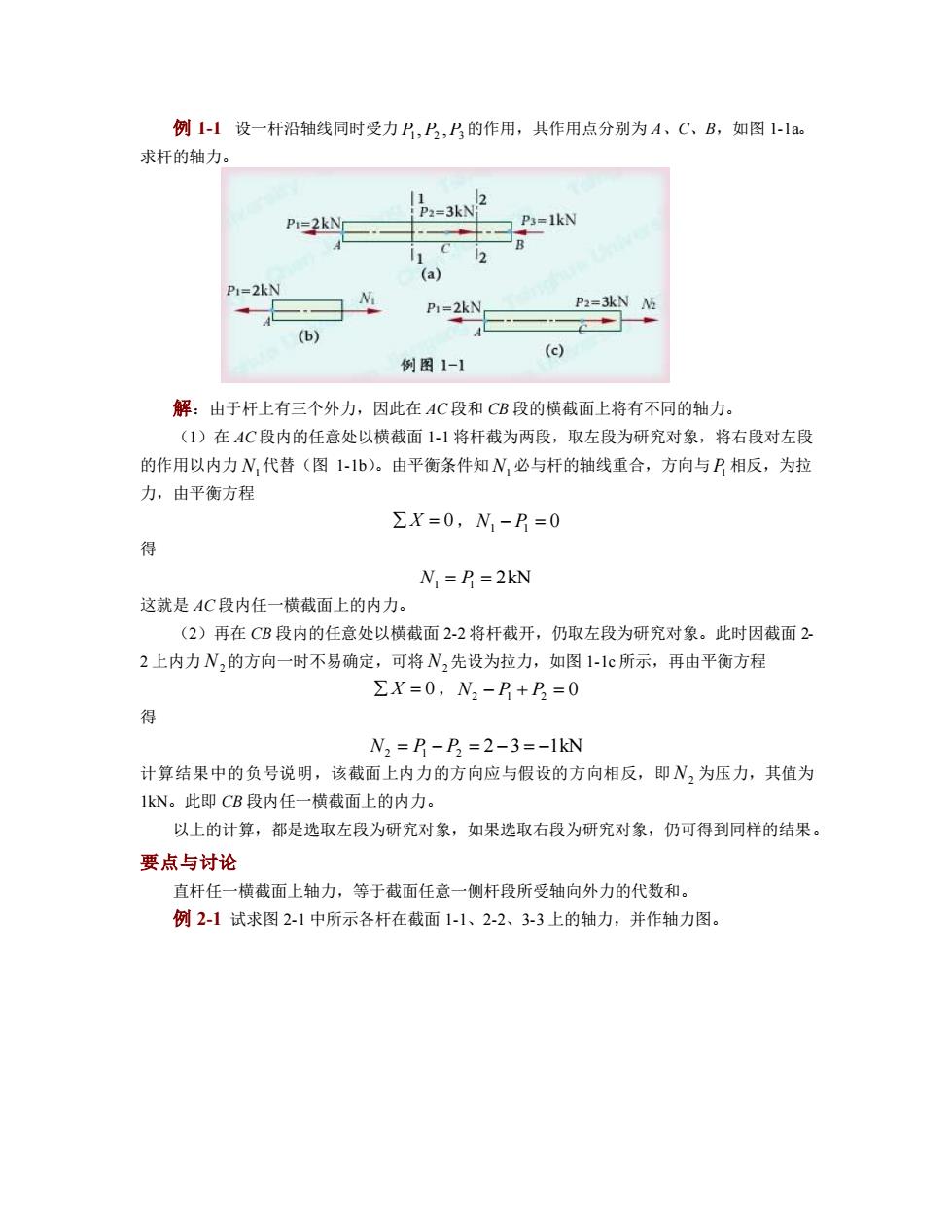
例 1-1 设一杆沿轴线同时受力 1 2 3 P , P ,P 的作用,其作用点分别为 A、C、B,如图 1-1a。 求杆的轴力。 解:由于杆上有三个外力,因此在 AC 段和 CB 段的横截面上将有不同的轴力。 (1)在 AC 段内的任意处以横截面 1-1 将杆截为两段,取左段为研究对象,将右段对左段 的作用以内力 N1 代替(图 1-1b)。由平衡条件知 N1 必与杆的轴线重合,方向与 P1 相反,为拉 力,由平衡方程 X = 0 , N1 − P1 = 0 得 N1 = P1 = 2kN 这就是 AC 段内任一横截面上的内力。 (2)再在 CB 段内的任意处以横截面 2-2 将杆截开,仍取左段为研究对象。此时因截面 2- 2 上内力 N2 的方向一时不易确定,可将 N2 先设为拉力,如图 1-1c 所示,再由平衡方程 X = 0 , N2 − P1 + P2 = 0 得 N2 = P1 − P2 = 2 −3 = −1kN 计算结果中的负号说明,该截面上内力的方向应与假设的方向相反,即 N2 为压力,其值为 1kN。此即 CB 段内任一横截面上的内力。 以上的计算,都是选取左段为研究对象,如果选取右段为研究对象,仍可得到同样的结果。 要点与讨论 直杆任一横截面上轴力,等于截面任意一侧杆段所受轴向外力的代数和。 例 2-1 试求图 2-1 中所示各杆在截面 1-1、2-2、3-3 上的轴力,并作轴力图
解:(1)求各截面轴力 截面11由左段(图b)的平衡条件 -(a) ΣX=0,N1=0 截面2-2由左段(图c)的平衡条件 6) ΣX=0,N2=2P(拉) (c) 截面3-3由左段(图d)的平衡条件 ∑X=0,N3=2P-P=P(拉) (2)作轴力图 由所得各截面的轴力,可作杆的轴力图 2外 (e) 如图e所示。 例图2-1 要点与讨论 1.在求杆件的轴力时,一般应先计算杆件的未知外力(包括支座反力)。 2.在本题中,若始终取截面的左段来考虑,则可不求A端支座反力。 例2-2图2-2所示较接正方形结构,各杆的横截面面积都等于25cm2,材料均为铸铁,其 许用拉应力[o,]=35MNm2,许用压应力口,=150MNhm',试求结构的许可载荷。 解:(1)求各杆轴力 由节点B(图2-2b)的平衡 条件 ∑X=0 P-2N1cos45°=0, (b) 例图2-2 由节点A(图2-2c)的平衡条件 N2-2N1cos45°=0,N2=P(压) (2)许可载荷 由斜杆的拉伸强度条件 所以 P≤24[o,]=V2×25×10)x35x10)=123.7kN 由铅垂杆的压缩强度条件
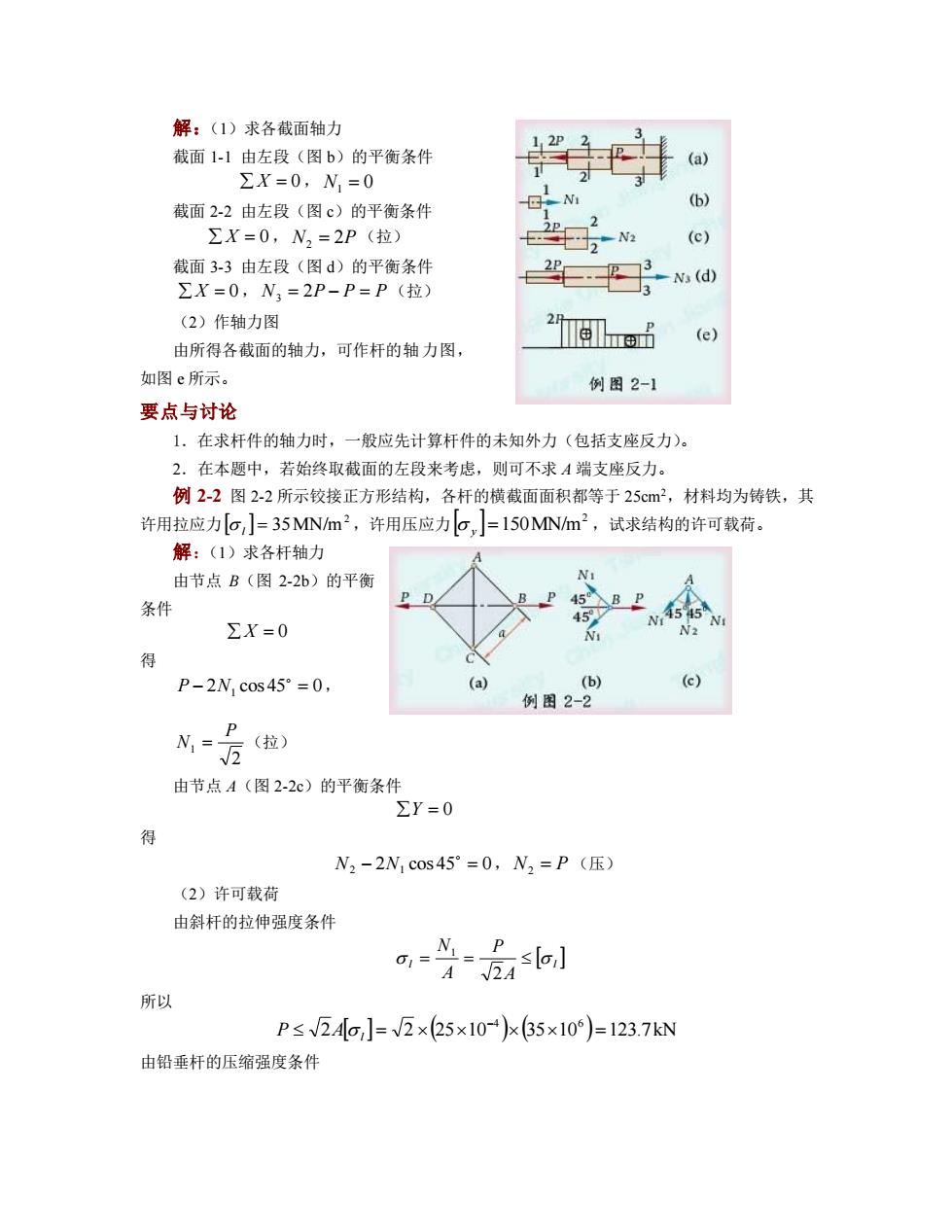
解:(1)求各截面轴力 截面 1-1 由左段(图 b)的平衡条件 X = 0 , N1 = 0 截面 2-2 由左段(图 c)的平衡条件 X = 0, N2 = 2P (拉) 截面 3-3 由左段(图 d)的平衡条件 X = 0, N3 = 2P − P = P (拉) (2)作轴力图 由所得各截面的轴力,可作杆的轴力图, 如图 e 所示。 要点与讨论 1.在求杆件的轴力时,一般应先计算杆件的未知外力(包括支座反力)。 2.在本题中,若始终取截面的左段来考虑,则可不求 A 端支座反力。 例 2-2 图 2-2 所示铰接正方形结构,各杆的横截面面积都等于 25cm2,材料均为铸铁,其 许用拉应力 MN/m2 l = 35 ,许用压应力 MN/m2 y =150 ,试求结构的许可载荷。 解:(1)求各杆轴力 由节点 B(图 2-2b)的平衡 条件 X = 0 得 − 2 1 cos45 = 0 P N , 2 1 P N = (拉) 由节点 A(图 2-2c)的平衡条件 Y = 0 得 2 − 2 1 cos 45 = 0 N N , N2 = P (压) (2)许可载荷 由斜杆的拉伸强度条件 l l A P A N = = 2 1 所以 2 2 (25 10 ) (35 10 ) 123.7kN 4 6 = = − P A l 由铅垂杆的压缩强度条件

as 所以 P≤A4ol=25x10-+)x35x105)=375kN 故结构的许可载荷为[P]=123.7kN 要点与讨论 1,尽管拉力N,要比压力N,小约40%,但结构的许可载荷还是受拉伸强度所限制。这是 因为铸铁的抗拉强度要比其抗压强度低得多。 2.在工程实际中,受压构件通常选用铸铁等脆性材料,而受拉构件一般选用低碳钢等塑 性材料,以合理地利用各种材料的机械性能。 例23图23所示结构,杆AB和BC的抗拉刚度EA相同,在节点B处承受集中载荷P, 试求节点B的水平及铅垂位移。 解:(1)求各杆轴力 由节点B(图2-3b)的平衡 条件 ΣX=0,ΣY=0 人45 N2cos45°-N,=0 N2sin45°-P=0 解得 (a) N1=P,N2=√2P B45 N (2)求各杆变形 杆AB (b) 杆BC 例图2-3 N.-Nh=VpxVa_2Pa EA EA (伸长) (3)节点B的位移 结构变形后,两杆仍应相交在一点,这就是变形的相容条件,作结构的变形图(图2-3c): 沿杆AB的延长线量取BB:等于△,沿杆CB的延长线量取BB2等于M2,分别在点B1和处 作BB,和BB,的垂线,两垂线的交点B'为结构变形后节点B应有的新位置。也即,结构变形后 成为AB'C的形状。图2-3c称为结构的变形图。 为求节点B的位移,也可单独作出节点B的位移图。位移图的作法与变形图作法类似,如 图2-3d所示
y A P A N = = 2 2 所以 (25 10 ) (35 10 ) 375kN 4 6 = = − P A y 故结构的许可载荷为 P =123.7kN 要点与讨论 1.尽管拉力 N1 要比压力 N2 小约 40%,但结构的许可载荷还是受拉伸强度所限制。这是 因为铸铁的抗拉强度要比其抗压强度低得多。 2.在工程实际中,受压构件通常选用铸铁等脆性材料,而受拉构件一般选用低碳钢等塑 性材料,以合理地利用各种材料的机械性能。 例 2-3 图 2-3 所示结构,杆 AB 和 BC 的抗拉刚度 EA 相同,在节点 B 处承受集中载荷 P, 试求节点 B 的水平及铅垂位移。 解:(1)求各杆轴力 由节点 B(图 2-3b)的平衡 条件 X = 0, Y = 0 得 N2 cos 45 − N1 = 0 N2 sin 45 − P = 0 解得 N1 = P, N2 = 2P (2)求各杆变形 杆 AB EA Pa EA N l l = = 1 1 1 (伸长) 杆 BC EA Pa EA P a EA N l l 2 2 2 2 2 2 = = = (伸长) (3)节点 B 的位移 结构变形后,两杆仍应相交在一点,这就是变形的相容条件,作结构的变形图(图 2-3c): 沿杆 AB 的延长线量取 BB1 等于 1 l ,沿杆 CB 的延长线量取 BB2等于 2 l ,分别在点 B1和B2处 作 BB1 和 BB2的垂线,两垂线的交点 B 为结构变形后节点 B 应有的新位置。也即,结构变形后 成为 ABC 的形状。图 2-3c 称为结构的变形图。 为求节点 B 的位移,也可单独作出节点 B 的位移图。位移图的作法与变形图作法类似,如 图 2-3d 所示

结构的变形图和节点的位移图,在计算节点位移中是等价的。在今后的计算中,可根据具 体情况,选作一图。 由位移图的几何关系,可得 水平位移 =照=出-留) 铅垂位移 名g+如59}会=62贤山 P4=BB=△ 要点与讨论 1.在载荷P作用下,由于两杆长度改变,导致节点B发生位移,两杆方位改变,夹角不 再为45°,如果按45°求解,则两杆的轴力之值与实际数值尚有差异,不过由于杆长的改变量 很小(在弹性范围内,£值很小),以致两杆方位的改变量很小,从而对轴力的值影响很小, 所以不必考虑。 2.在一般问题中,常根据结构变形前的原始几何情况来计算各部分的内力,在拉伸、压 缩、扭转及弯曲等问题中均可如此处理。 例2-4图2-4a所示桁架,三杆AD、BD和CD具有相同的抗拉刚度EA,试求在铅垂载荷 P作用下各杆的轴力。 D D2 (a) (b) 例图2-4 解:(1)静力平衡条件 该桁架在力P作用下,可以判断:杆AD将受拉、杆CD将受压。但杆BD在事先将难以 判断,我们可以任意假定。若假定杆BD受拉,则由节点D(图24b)的平衡条件 X=0,N:cosa-N cosa-N:=0 ① EY=0,N sina+N:sina-P=0 ② (2)变形相容条件 作节点D的位移图(图2.4c),由几何关系 -2+ tana'sina 在作位移图时应该注意,杆件的变形应与受力图中杆件的轴力相对应。也就是说,在受力 图(图24b)中已假定杆AD和BD的轴力为拉力:杆CD为压力,则在位移图(图2-4c)中, 杆AD和BD的变形应是伸长,而杆CD应是缩短
结构的变形图和节点的位移图,在计算节点位移中是等价的。在今后的计算中,可根据具 体情况,选作一图。 由位移图的几何关系,可得 水平位移 ( ) = 1 = 1 = → EA Pa x BB l A 铅垂位移 (1 2 2) ( ) 2 tan 45 2 sin 45 1 2 + = + + = = = EA Pa EA Pa EA Pa l l y A BB 要点与讨论 1.在载荷 P 作用下,由于两杆长度改变,导致节点 B 发生位移,两杆方位改变,夹角不 再为 45 ,如果按 45 求解,则两杆的轴力之值与实际数值尚有差异,不过由于杆长的改变量 很小(在弹性范围内, 值很小),以致两杆方位的改变量很小,从而对轴力的值影响很小, 所以不必考虑。 2.在一般问题中,常根据结构变形前的原始几何情况来计算各部分的内力,在拉伸、压 缩、扭转及弯曲等问题中均可如此处理。 例 2-4 图 2-4a 所示桁架,三杆 AD、BD 和 CD 具有相同的抗拉刚度 EA,试求在铅垂载荷 P 作用下各杆的轴力。 解:(1)静力平衡条件 该桁架在力 P 作用下,可以判断:杆 AD 将受拉、杆 CD 将受压。但杆 BD 在事先将难以 判断,我们可以任意假定。若假定杆 BD 受拉,则由节点 D(图 2-4b)的平衡条件 X = 0 , N3 cos − N1 cos − N2 = 0 ① Y = 0 , N1 sin + N3 sin − P = 0 ② (2)变形相容条件 作节点 D 的位移图(图 2-4c),由几何关系 tan sin 2 sin 1 2 3 l l l + = 在作位移图时应该注意,杆件的变形应与受力图中杆件的轴力相对应。也就是说,在受力 图(图 2-4b)中已假定杆 AD和 BD的轴力为拉力;杆 CD为压力,则在位移图(图 2-4c)中, 杆 AD 和 BD 的变形应是伸长,而杆 CD 应是缩短

(3)物理关系 由胡克定律 NH EA EAsin a 4= N,H EA EAtano N NH 将物理关系代入变形相容条件,整理后得补充方程 N-N:=2N2 cos2a 联立方程①②③,解得各杆轴力为 N,-N,=2sing N,=0 要点与讨论 在本题中,由于结构的对称性,在铅垂载荷P的作用下,不难判断杆BD的轴力N2=O (节点D没有水平位移)。这样,杆AD与CD的轴力N,和N,就可直接由静力平衡条件求得, 从而将问题简化为静定问题。因此,在解决实际问题时,利用结构或载荷的对称性,往往能使 解题过程大为简化。 例3-1图3-1所示传动轴,齿轮与轴用平键联接,传递转矩M=4kNm。若键的尺寸 b=24mm、h=14mm,材料的许用剪应力[女]=80MN/m2,许用挤压应力口,=100 MN/m2,试求键的长度I。 (a) (c) 解:(1)受力分析 键的受力(图3-1b) P= M 2×4×103 d/280x10-3 -100kN (2)键的长度 由剪切强度条件 所以 100×103 1e0410x网52m
(3)物理关系 由胡克定律 sin 1 1 1 1 EA N H EA N l l = = tan 2 2 2 2 EA N H EA N l l = = sin 3 3 3 3 EA N H EA N l l = = 将物理关系代入变形相容条件,整理后得补充方程 2 1 3 2 N − N = 2N cos ③ 联立方程①②③,解得各杆轴力为 2sin 1 3 P N = N = , N3 = 0 要点与讨论 在本题中,由于结构的对称性,在铅垂载荷 P 的作用下,不难判断杆 BD 的轴力 N2 = 0 (节点 D没有水平位移)。这样,杆 AD与 CD的轴力 N1 和 N3 就可直接由静力平衡条件求得, 从而将问题简化为静定问题。因此,在解决实际问题时,利用结构或载荷的对称性,往往能使 解题过程大为简化。 例 3-1 图 3-1 所示传动轴,齿轮与轴用平键联接,传递转矩 M = 4 kNm。若键的尺寸 b = 24 mm、 h =14 mm,材料的许用剪应力 = 80 NNmm2,许用挤压应力 jy = 100 NNmm2,试求键的长度 l 。 解:(1)受力分析 键的受力(图 3-1b) 100 80 10 2 4 10 2 3 3 = = = − d M P kN (2)键的长度 由剪切强度条件 = = bl P A Q 所以 ( )( ) 52 24 10 80 10 100 10 3 6 3 = = − b P l mm