
For the trapezoidal rule,h=1 and f=f0+f0)=000+072159=086079 For Simpson's rule,h=1/2,and we get [/d1Uo+4yr3+70-g00o00+405152+072159=132I28 For Simpson's 3/8 rule,h=1/3,and we obtain u:0gU0+3g+3+0 =81.0000+30.69642)+302347)+0.72159)=131440 For Boole's rule,h=1/4,and the result is ea2go+2r-12n++7m 9071.0000)+320.6534)+120.55152)+3201.0666)+710.72159》=1.30859
For the trapezoidal rule, h=1 and For Simpson’s rule, h=1/2, and we get For Boole’s rule, h=1/4, and the result is For Simpson’s 3/8 rule, h=1/3, and we obtain 1 0 1 1 ( ) ( (0) (1)) (1.00000 0.72159) 0.86079 2 2 f x dx f f + = + = 1 0 1/ 2 1 1 ( ) ( (0) 4 ( ) (1)) (1.00000 4(1.55152) 0.72159) 1.32128 3 2 6 f x dx f f f + + = + + = 1 0 3(1/ 3) 1 2 ( ) ( (0) 3 ( ) 3 ( ) (1)) 8 3 3 1 (1.00000 3(1.69642) 3(1.23447) 0.72159) 1.31440 8 f x dx f f f f + + + = + + + = 1 0 2(1/ 4) 1 1 3 ( ) (7 (0) 32 ( ) 12 ( ) 32 ( ) 7 (1)) 45 4 2 4 1 (7(1.00000) 32(1.65534) 12(1.55152) 32(1.06666) 7(0.72159)) 1.30859 90 f x dx f f f f f + + + + = + + + + =
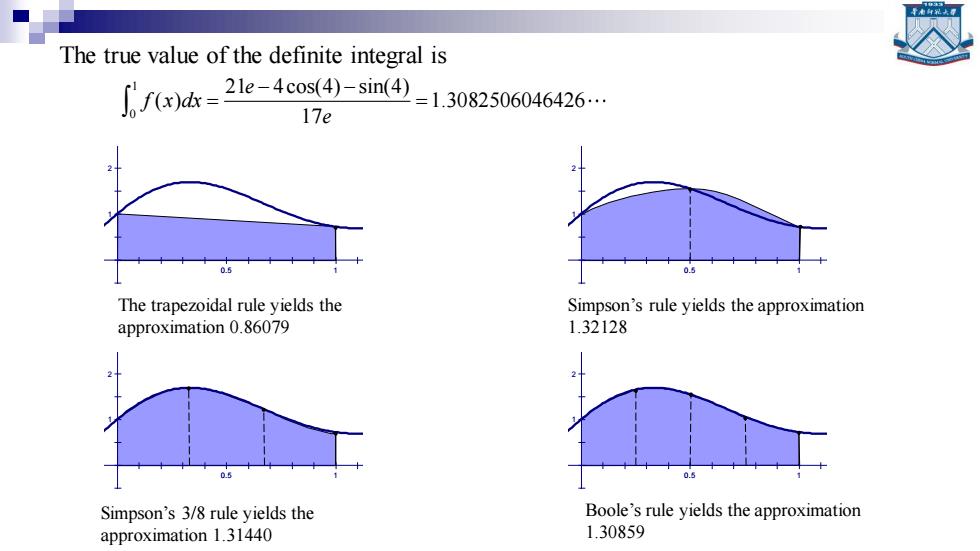
The true value of the definite integral is Jf0k-21e-4cs4-sim④-13082506046426 17e The trapezoidal rule yields the Simpson's rule yields the approximation approximation 0.86079 1.32128 08 0. Simpson's 3/8 rule yields the Boole's rule yields the approximation approximation 1.31440 1.30859
5 4 3 2 1 -1 -2 -3 -4 -5 0.5 1 1.5 2 2.5 5 4 3 2 1 -1 -2 -3 -4 -5 0.5 1 1.5 2 2.5 5 4 3 2 1 -1 -2 -3 -4 -5 0.5 1 1.5 2 2.5 5 4 3 2 1 -1 -2 -3 -4 -5 0.5 1 1.5 2 2.5 The trapezoidal rule yields the approximation 0.86079 Boole’s rule yields the approximation 1.30859 Simpson’s rule yields the approximation 1.32128 The true value of the definite integral is 1 0 21 4cos(4) sin(4) ( ) 1.3082506046426 17 e f x dx e − − = = Simpson’s 3/8 rule yields the approximation 1.31440