
Quadrature Formulas Based on Polynomial Interpolation There exists a unique polynomial Pux)of degree <M passing through the M+1 equally spaced points {(xf()).When this polynomial is used to approximate f(x)over [a,b],and then the integral off(x)is approximated by the integral of Px),the resulting formula is called a Newton-Cotes quadrature formula When the sample points xo-a and xb are used,it is called a closed Newton-Cotes formula
Quadrature Formulas Based on Polynomial Interpolation ◼ There exists a unique polynomial PM(x) of degree ≤M passing through the M+1 equally spaced points . When this polynomial is used to approximate f (x) over [a,b], and then the integral of f (x) is approximated by the integral of PM(x), the resulting formula is called a Newton-Cotes quadrature formula. When the sample points x0 =a and xM =b are used, it is called a closed Newton-Cotes formula. 0 {( , ( ))}M k k k x f x =

Closed Newton-Cotes Formulas Thm.5.1.Assume thatx=x+kh are equally spaced nodes andx).The first four closed Newton-Cotes quadrature formulas are fe达=96+0 (trapezoidal rule) f达*6+4f+) (Simpson's rule) e*+3++) (Simpson's 3/8 rule) 1a=治%+2+12听+2+7 (Boole's rule)
Closed Newton-Cotes Formulas 1 0 0 1 ( ) ( ) 2 x x h f x dx f f + 2 0 0 1 2 ( ) ( 4 ) 3 x x h f x dx f f f + + 3 0 0 1 2 3 3 ( ) ( 3 3 ) 8 x x h f x dx f f f f + + + Thm. 5.1. Assume that xk=x0+kh are equally spaced nodes and fk=f(xk ). The first four closed Newton-Cotes quadrature formulas are 4 0 0 1 2 3 4 2 ( ) (7 32 12 32 7 ) 45 x x h f x dx f f f f f + + + + (trapezoidal rule) (Simpson’s rule) (Simpson’s 3/8 rule) (Boole’s rule)

Integral Results from the N-C Formulas Example 5.1.Consider the function fx)=1+e*sin(4x),the equally spaced quadrature nodes xo-0.0,x1=0.5,x2=1.0,x3=1.5,and x4-=2.0,and the corresponding function values=1.00000,f=1.55152,=0.72159, =0.93765,and fa=1.13390.The step size is h=0.5. fa:00w0+15152=06378 [fk*051000+405152+0.72159=132128 [fd301000+315152+0.72159+093765)=164193 8 fxk÷2X0.3(71.000)+3215152+120.72159)+320.93765)+701.13390)=22944 45
Integral Results from the N-C Formulas Example 5.1. Consider the function f(x)=1+e -x sin(4x), the equally spaced quadrature nodes x0=0.0, x1=0.5,x2=1.0,x3=1.5, and x4=2.0, and the corresponding function values f0=1.00000, f1=1.55152, f2=0.72159, f3=0.93765, and f4=1.13390. The step size is h=0.5. 0.5 0 0.5 ( ) (1.00000 1.55152) 0.63788 2 f x dx + = 1.0 0 0.5 ( ) (1.00000 4(1.55152) 0.72159) 1.32128 3 f x dx + + = 1.5 0 3(0.5) ( ) (1.00000 3(1.55152) 3(0.72159) 0.93765) 1.64193 8 f x dx + + + = 2.0 0 2(0.5) ( ) (7(1.00000) 32(1.55152) 12(0.72159) 32(0.93765) 7(1.13390)) 2.29444 45 f x dx + + + + =
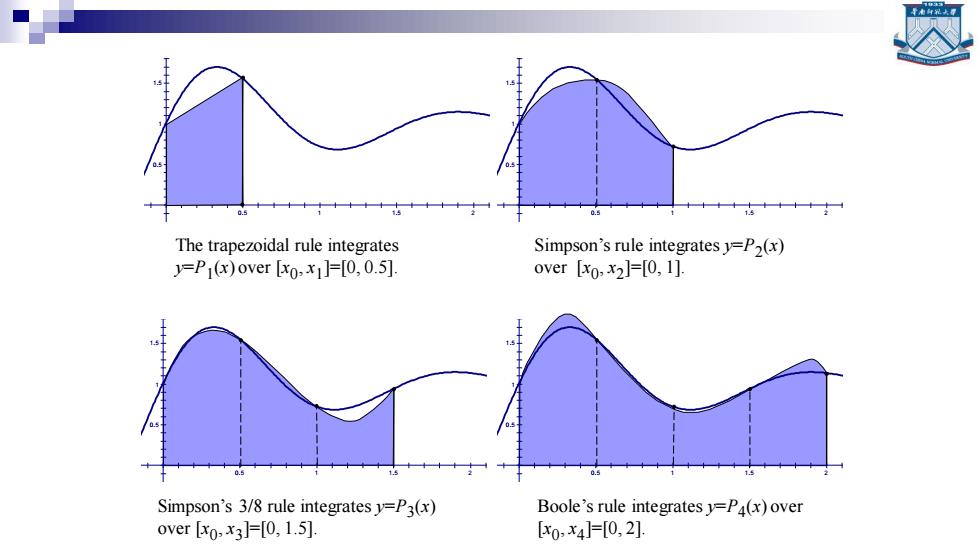
The trapezoidal rule integrates Simpson's rule integrates y=P2(x) =P(x)over [xo,x1]=[0,0.5]. over [xo,x2]=[0,1]. Simpson's 3/8 rule integrates y=P3(x) Boole's rule integrates y=P4(x)over over[xo,x3]F[0,1.5]. [x0,x4]=0,2]
3.5 3 2.5 2 1.5 1 0.5 -0.5 -1 -1.5 -2 -2.5 -0.5 0.5 1 1.5 2 2.5 3 3.5 3.5 3 2.5 2 1.5 1 0.5 -0.5 -1 -1.5 -2 -2.5 -0.5 0.5 1 1.5 2 2.5 3 3.5 3.5 3 2.5 2 1.5 1 0.5 -0.5 -1 -1.5 -2 -2.5 -0.5 0.5 1 1.5 2 2.5 3 3.5 3.5 3 2.5 2 1.5 1 0.5 -0.5 -1 -1.5 -2 -2.5 -0.5 0.5 1 1.5 2 2.5 3 3.5 The trapezoidal rule integrates y=P1 (x) over [x0 , x1 ]=[0, 0.5]. Boole’s rule integrates y=P4 (x) over [x0 , x4 ]=[0, 2]. Simpson’s 3/8 rule integrates y=P3 (x) over [x0 , x3 ]=[0, 1.5]. Simpson’s rule integrates y=P2 (x) over [x0 , x2 ]=[0, 1]

The Degree of Precision of A Quadrature Formula Def.5.2.The degree ofprecision of a quadrature formula is the positive integer n such that E[P ]0 for all polynomials P(x)of degree isn,but for which E[P]t0 for some polynomial P(x)of degree n+1. The form of E[P]can be anticipated by studying what happens when f(x)is a polynomial.Consider the arbitrary polynomial P(x)=ax+a+...+ax+ao of degree i. If isn,then P((x)=0 for allx,and P(x)=(n+1)a for all x. Thus the general form for the truncation error is E[f]=kf(D(c),where K is a suitably chosen constant and n is the degree of precision. Note:The definition of the degree of precision of a quadrature formula doesn't specify the integral interval
The Degree of Precision of A Quadrature Formula ◼ Def. 5.2. The degree of precision of a quadrature formula is the positive integer n such that E[Pi ]=0 for all polynomials Pi (x) of degree i≤n, but for which E[Pn+1] ≠0 for some polynomial Pn+1(x) of degree n+1. The form of E[Pi ] can be anticipated by studying what happens when f (x) is a polynomial. Consider the arbitrary polynomial Pi (x)=aix i+ai-1x i-1+…+a1x+a0 of degree i. If i≤n, then Pi (n+1)(x)≡0 for all x, and for all x. ( 1) 1 1 ( ) ( 1)! n P x n a n n + + + = + Thus the general form for the truncation error is E[ f ]=K f (n+1)(c), where K is a suitably chosen constant and n is the degree of precision. Note: The definition of the degree of precision of a quadrature formula doesn’t specify the integral interval