
□上次课复习: 1、构成时间数列的基本要素有哪些?编制时间数列应遵循哪些基 本原则? 2、计算平均发展速度的水平法和累计法有何不同? 3、时间数列的各影响因素的含义是什么? 口本次课题:第七章统计指数(8课时) 口教学过程: 1.导入新课 2.讲授新课 3.总结及布置练习 口讲授内容: 自写引音:通过讲述上月GPI指数引入新课。 导入新课: 指标用来反映经济现象的数量特征,是统计工作的一个必然 目标,是进行统计分析的基础。那么:在第四章,我们学习了根 据总体资料,编制总量指标,平均指标及变异指标,相对指标等。 在第五章,我们掌握了根据样本资料,在允许误差的概率保证程 度下,对总体指标进行估计分析。在第六章,我们学习了对同一 个总体下,单位不同标志之间的相关,因果关系,运用相关,回 归分析两变量之间的密切程度。相同的是这三章内容中反映的指
1 上次课复习: 1、构成时间数列的基本要素有哪些?编制时间数列应遵循哪些基 本原则? 2、计算平均发展速度的水平法和累计法有何不同? 3、时间数列的各影响因素的含义是什么? 本次课题: 第七章 统计指数(8 课时) 教学过程: 1.导入新课 2.讲授新课 3.总结及布置练习 讲授内容: 引言:通过讲述上月 CPI 指数引入新课。 导入新课: 指标用来反映经济现象的数量特征,是统计工作的一个必然 目标,是进行统计分析的基础。那么:在第四章,我们学习了根 据总体资料,编制总量指标,平均指标及变异指标,相对指标等。 在第五章,我们掌握了根据样本资料,在允许误差的概率保证程 度下,对总体指标进行估计分析。在第六章 ,我们学习了对同一 个总体下,单位不同标志之间的相关,因果关系,运用相关,回 归分析两变量之间的密切程度。相同的是这三章内容中反映的指

标都是特定时间的指标值,但是我们知道,作为反映经济活动的 各项指标随着各方面的约束,在时间推移条件下,是回发生变化 的。例如,密云县1998年GDP为2.8亿元,1999年为2.9亿元, 2.8亿元,2.9亿元均是指标值,但是时间不同,指标值发生了变 化: 1、99年比98年增加了0.1亿元(2.9-2.8) 2、99年比98年增加了(2.9/2.8)-1=3.57% 本讲中,我们主要讲的就是关于指标在两个时间上的变化。一 指数 讲授新课: 一.指数的涵义及分类(2课时) 1指数的涵义 (1)简单现象总体:总体中的单位数或标志值可以直接相 加的总体。 (2)复杂现象总体:构成总体的单位数急标志值不能直接 相加。 (3)广义指数的涵义:凡是表明社会经济现象数量变动的 相对数。 (4)狭义的指数涵义:综合反映在复杂现象总体中不能直 接相加的各种事物在数量上的总变动。 2指数的表现形式:某一时期的指标(报告期)/另一时期的指 标(基期)。分子分母属性完全相同,所以是相对数,无名数 2
2 标都是特定时间的指标值,但是我们知道,作为反映经济活动的 各项指标随着各方面的约束,在时间推移条件 下,是回发生变化 的。例如,密云县 1998 年 GDP 为 2.8 亿元,1999 年为 2.9 亿元, 2.8 亿元,2.9 亿元均是指标值,但是时间不同,指标值发生了变 化: 1、99 年比 98 年增加了 0.1 亿元(2.9-2.8) 2、99 年比 98 年增加了(2.9/2.8)-1=3.57% 本讲中,我们主要讲的就是关于指标在两个时间上的变化。—— 指数 讲授新课: 一. 指数的涵义及分类(2 课时) 1 指数的涵义 (1) 简单现象总体:总体中的单位数或标志值可以直接相 加的总体。 (2) 复杂现象总体:构成总体的单位数急标志值不能直接 相加。 (3) 广义指数的涵义:凡是表明社会经济现象数量变动的 相对数。 (4) 狭义的指数涵义:综合反映在复杂现象总体中不能直 接相加的各种事物在数量上的总变动。 2 指数的表现形式:某一时期的指标(报告期)/另一时期的指 标(基期)。分子分母属性完全相同,所以是相对数,无名数

3指数的作用教材311(注意简答题) 4指数的种类(简答题,填空题,单选题) (1)按其所反映的对象范围的不同划分为:个体指数和总 指数 (2)按其反映的指标性质不同分为:数量指标指数和质量 指标指数 (3)按照采用的基期不同,分为:定基指数和环比指数 (4)按其计算方法和计算公式的表现形式不同,分为:总 量指标指数和平均指标指数。 二、指数的编制 (一)综合指数(2课时) 请学生判断实例 产品 Q Q0 Q1 CO P1 甲(件) 2000 2200 10.5 10.0 12.0 12.5 乙(斤)5000 6000 6.0 5.5 6.2 6.0 (1)现象总体的类型:复杂现象总体
3 3 指数的作用 教材 311(注意简答题) 4 指数的种类(简答题,填空题,单选题) (1) 按其所反映的对象范围的不同划分为:个体指数和总 指数 (2) 按其反映的指标性质不同分为:数量指标指数和质量 指标指数 (3) 按照采用的基期不同,分为:定基指数和环比指数 (4) 按其计算方法和计算公式的表现形式不同,分为:总 量指标指数和平均指标指数。 二、指数的编制 (一)综合指数(2 课时) 请学生判断实例 (1 )现象总体的类型:复杂现象总体 产品 Q C P Q0 Q1 C0 C1 P0 P1 甲(件) 乙(斤) 2000 5000 2200 6000 10.5 6.0 10.0 5.5 12.0 6.2 12.5 6.0

(2)不能简单相加,若要判断企业单位成本,价格等的变化, 应该怎么办? 引入课题:我们换一个角度来看,其价格和成本不能直接相加, 但如果我们利用M(销售额)=PQ,就可以将其相加,然后利 用销售额的变化来说明价格的变化。那么在这个过程中,为了 充分说明价格大变化,应将Q值固定在某一个时期,从而说明 P的变动。由此,我们可以概括出: 1综合指数的特点 (1)从现象联系分析中,来确定与我们所要研究的现象相 联系的因素,即同度量因素。 (2)对复杂现象总体包括的两个因素,把其中一个因素, 即同度量因素或权数加以固定,以便消除其变化,来 测定我们所要研究的哪个因素即指标的变动。 2同度量因素 (1)涵义使得不同度量单位的现象总体转化为可以加总并客 观上体现它在实际经济现象或过程中的份额和比重。 (2)作用同度量作用,权数作用。 3综合指数的编制
4 (2) 不能简单相加,若要判断企业单位成本,价格等的变化, 应该怎么办? 引入课题:我们换一个角度来看,其价格和成本不能直接相加, 但如果我们利用 M(销售额)=P*Q,就可以将其相加,然后利 用销售额的变化来说明价格的变化。那么在这个过程中,为了 充分说明价格大变化,应将 Q 值固定在某一个时期,从而说明 P 的变动。由此,我们可以概括出: 1 综合指数的特点 (1) 从现象联系分析中,来确定与我们所要研究的现象相 联系的因素,即同度量因素。 (2) 对复杂现象总体包括的两个因素,把其中一个因素, 即同度量因素或权数加以固定,以便消除其变化,来 测定我们所要研究的哪个因素即指标的变动。 2 同度量因素 (1)涵义 使得不同度量单位的现象总体转化为可以加总并客 观上体现它在实际 经济现象或过程中的份额和比重。 (2) 作用 同度量作用,权数作用。 3 综合指数的编制
(1)拉氏公式和帕氏公式 拉思佩雷主张将权数固定在基期(0), 帕舍主张将权数固定在报告期(1) (2)编制方法:数量指标指数按拉氏公式来编制,即选择质 量指标作为同度量因素,并且把它固定在基期,质量指标指 数的编制按帕氏公式来编制,即选择数量指标作为同度量因 素,并且把它固定在计算期 即K=Σp1q1÷pqu Ko=2PQ÷ΣPQo 例题:某市几种主要副食品价格和销售量的资料如下: 副 基期 计算期 价格 销售 价格 销售 PO 量Q0 量Q1 P1Q1 POQ1 POQ0 蔬菜2.1 1.00 2.3 5.20 11.96 10.92 10.5 牛肉 17.0 4.46 17.8 5.52 98.26 93.84 75.82 鲜蛋 9.0 1.20 9.2 1.15 10.58 10.35 10.8 水产 16.5 1.15 18.0 1.30 23.4 21.45 18.97 品 5
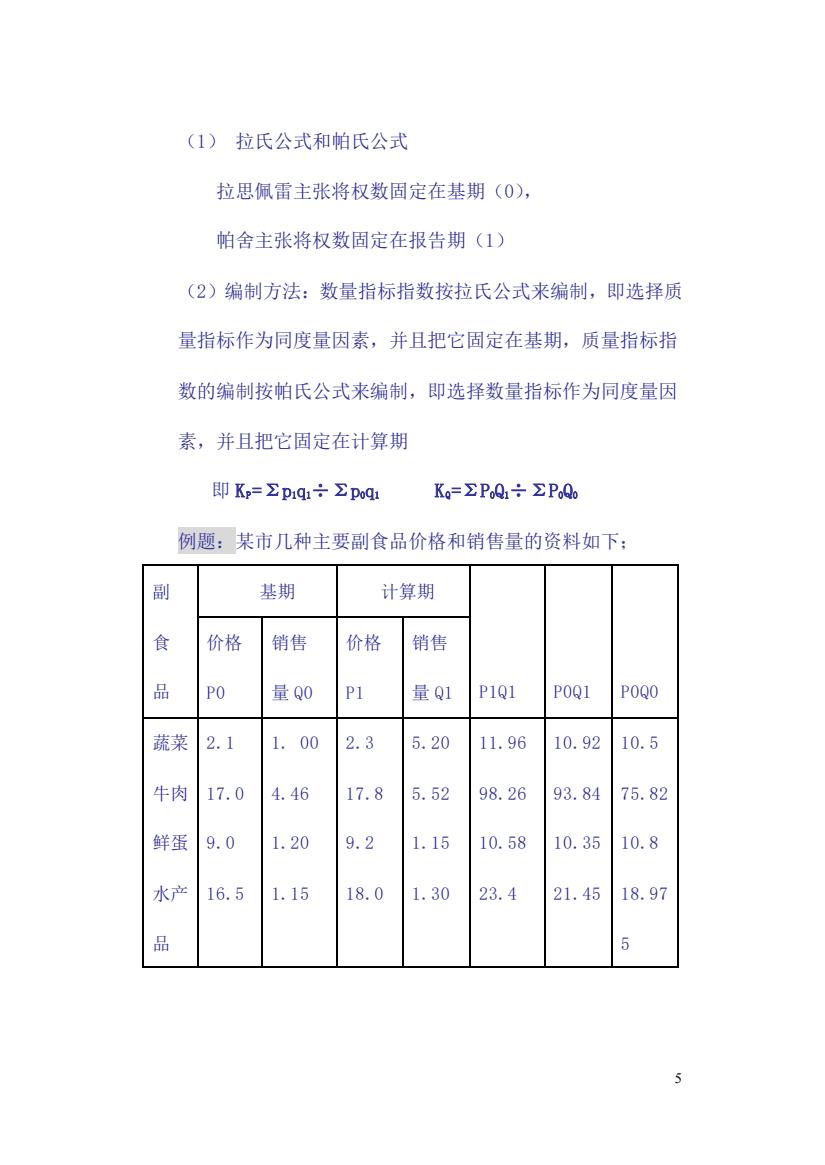
5 (1) 拉氏公式和帕氏公式 拉思佩雷主张将权数固定在基期(0), 帕舍主张将权数固定在报告期(1) (2)编制方法:数量指标指数按拉氏公式来编制,即选择质 量指标作为同度量因素,并且把它固定在基期,质量指标指 数的编制按帕氏公式来编制,即选择数量指标作为同度量因 素,并且把它固定在计算期 即 KP=Σp1q1÷Σp0q1 KQ=ΣP0Q1÷ΣP0Q0 例题:某市几种主要副食品价格和销售量的资料如下; 副 食 品 基期 计算期 P1Q1 P0Q1 P0Q0 价格 P0 销售 量 Q0 价格 P1 销售 量 Q1 蔬菜 牛肉 鲜蛋 水产 品 2.1 17.0 9.0 16.5 1. 00 4.46 1.20 1.15 2.3 17.8 9.2 18.0 5.20 5.52 1.15 1.30 11.96 98.26 10.58 23.4 10.92 93.84 10.35 21.45 10.5 75.82 10.8 18.97 5