
白上次课复习: 1、什么是抽样平均误差?其影响因素有哪些? 2、什么是抽样极限误差,它与抽样平均误差有何关系? 3、抽样平均误差与抽样极限误差在抽样估计中各自发挥着什么作 用? □本次课题:第八章相关与回归分析(8课时) 口教学过程: 1.导入新课 2.讲授新课 3.总结及布置练习 □讲授内容: e 号引言:通过展示一份网络调查问卷引入新课。 导入新课: 在前面章节中,我们己经学习了分析总体特征的一些方法, 通过指标可以说明总体的具体数量特征,用抽样估计解决了无法 进行全面调查统计的难题。但是在一项统计活动中,我们不但要 了解某个总体或某些总体的特征,还要了解一些总体之间的联系 以及互相影响的程度。如下例: 1
1 上次课复习: 1、什么是抽样平均误差?其影响因素有哪些? 2、什么是抽样极限误差,它与抽样平均误差有何关系? 3、抽样平均误差与抽样极限误差在抽样估计中各自发挥着什么作 用? 本次课题: 第八章 相关与回归分析(8 课时) 教学过程: 1.导入新课 2.讲授新课 3.总结及布置练习 讲授内容: 引言:通过展示一份网络调查问卷引入新课。 导入新课: 在前面章节中,我们已经学习了分析总体特征的一些方法, 通过指标可以说明总体的具体数量特征,用抽样估计解决了无法 进行全面调查统计的难题。但是在一项统计活动中,我们不但要 了解某个总体或某些总体的特征,还要了解一些总体之间的联系 以及互相影响的程度。如下例:
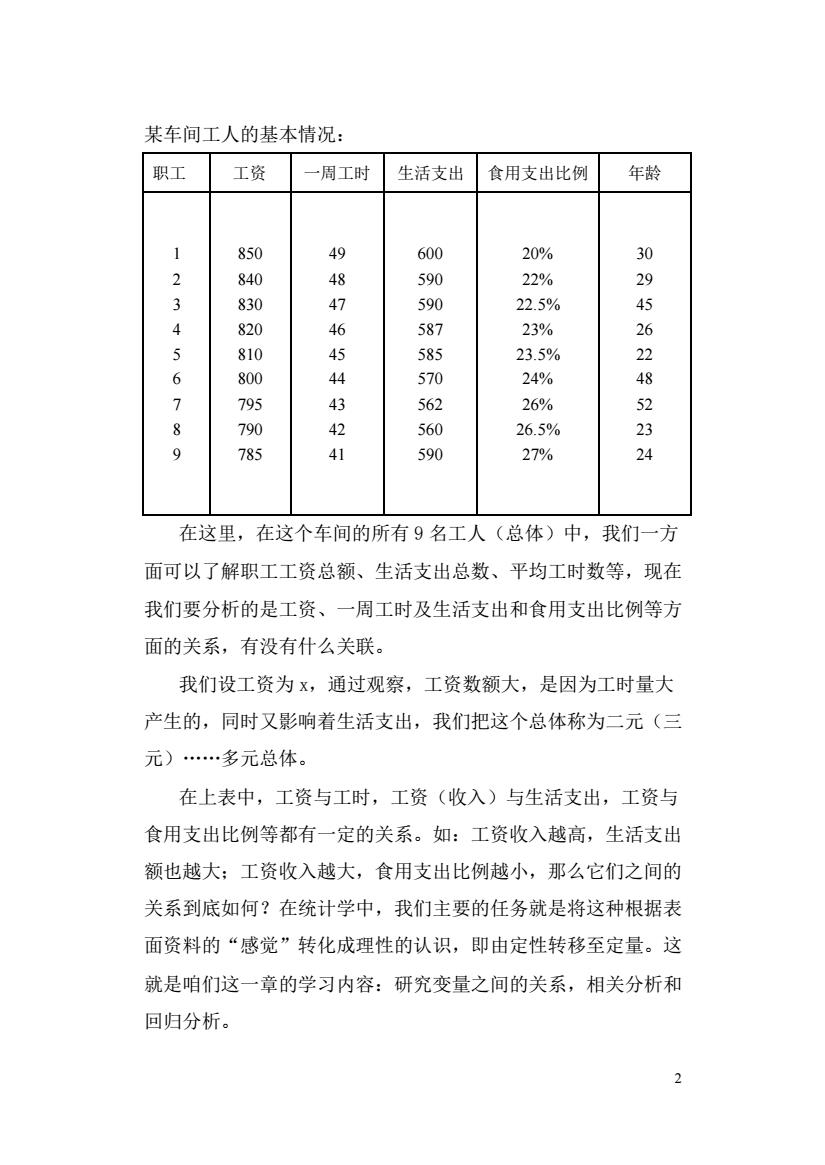
某车间工人的基本情况: 职工 工资 一周工时生活支出 食用支出比例 年龄 850 49 600 20% 30 8 48 590 22% 3 830 590l 2.5% 5 820 6 87 23% 5 810 58 235% 22 6 800 570 24% 8 7 43 562 26% 52 9 7 124 560 26.5% 23 590 27% 24 在这里,在这个车间的所有9名工人(总体)中,我们一方 面可以了解职工工资总额、生活支出总数、平均工时数等,现在 我们要分析的是工资、一周工时及生活支出和食用支出比例等方 面的关系,有没有什么关联。 我们设工资为x,通过观察,工资数额大,是因为工时量大 产生的,同时又影响着生活支出,我们把这个总体称为二元(三 元).多元总体。 在上表中,工资与工时,工资(收入)与生活支出,工资与 食用支出比例等都有一定的关系。如:工资收入越高,生活支出 额也越大:工资收入越大,食用支出比例越小,那么它们之间的 关系到底如何?在统计学中,我们主要的任务就是将这种根据表 面资料的“感觉”转化成理性的认识,即由定性转移至定量。这 就是咱们这一章的学习内容:研究变量之间的关系,相关分析和 回归分析
2 某车间工人的基本情况: 职工 工资 一周工时 生活支出 食用支出比例 年龄 1 2 3 4 5 6 7 8 9 850 840 830 820 810 800 795 790 785 49 48 47 46 45 44 43 42 41 600 590 590 587 585 570 562 560 590 20% 22% 22.5% 23% 23.5% 24% 26% 26.5% 27% 30 29 45 26 22 48 52 23 24 在这里,在这个车间的所有 9 名工人(总体)中,我们一方 面可以了解职工工资总额、生活支出总数、平均工时数等,现在 我们要分析的是工资、一周工时及生活支出和食用支出比例等方 面的关系,有没有什么关联。 我们设工资为 x,通过观察,工资数额大,是因为工时量大 产生的,同时又影响着生活支出,我们把这个总体称为二元(三 元).多元总体。 在上表中,工资与工时,工资(收入)与生活支出,工资与 食用支出比例等都有一定的关系。如:工资收入越高,生活支出 额也越大;工资收入越大,食用支出比例越小,那么它们之间的 关系到底如何?在统计学中,我们主要的任务就是将这种根据表 面资料的“感觉”转化成理性的认识,即由定性转移至定量。这 就是咱们这一章的学习内容:研究变量之间的关系,相关分析和 回归分析

讲授新课: 一.相关分析(4课时) (一)相关分析的含义: 对总体中确实具有联系的标志进行分析,其主体是对总 体中具有因果关系标志的分析。有两种类型的分析: 1.函数关系:这是一个典型的数学概念,反映的是一个变 量数值随着另一个变量的给定也确定下来(完全依存 关系)。 如:c=2πR 只要知道圆的半径R的值(R=3), 则马上可知道该圆周长(C=6π) M=P×Q设一条毛巾价格为5元/条, 则销售5条的销售额为25元。 2、相关关系:是一种不完全确定的随机关系。 如:设一块田的面积,长度是固定的1,如果每株的间 隔是变量x,则一列栽苗的株数则是间隔变量的函 数:n=1/x 但是一株苗的粮食产量则不是间隔变量的一个函数,不 能随机被确定,但是又受它的影响,这种变量之间的关系则 称相关关系。 3.函数关系与相关关系的关系 1)区别:定义上的区别 一个是完全的依存关系,一个则是不完全依存关系
3 讲授新课: 一. 相关分析(4 课时) (一)相关分析的含义: 对总体中确实具有联系的标志进行分析,其主体是对总 体中具有因果关系标志的分析。有两种类型的分析: 1.函数关系:这是一个典型的数学概念,反映的是一个变 量数值随着另一个变量的给定也确定下来(完全依存 关系)。 如: c = 2R 只要知道圆的半径 R 的值(R=3), 则马上可知道该圆周长(C=6π)。 M = PQ 设一条毛巾价格为 5 元/条, 则销售 5 条的销售额为 25 元。 2、相关关系:是一种不完全确定的随机关系。 如:设一块田的面积,长度是固定的 l ,如果每株的间 隔是变量 x,则一列栽苗的株数则是间隔变量的函 数:n=l/x 但是一株苗的粮食产量则不是间隔变量的一个函数,不 能随机被确定,但是又受它的影响,这种变量之间的关系则 称相关关系。 3.函数关系与相关关系的关系 1) 区别:定义上的区别。 一个是完全的依存关系,一个则是不完全依存关系

2)联系:相关关系是相关分析的研究对象 函数关系是相关分析的工具 (二)相关的种类 1.按相关的程度分为完全相关和不完全相关,不相关 2.按相关的方向分为正相关和负相关 3.按相关的形式分为线性相关和非线性相关。 对应数值的图形近似一条直线 4.按影响因素的多少可分为单相关和复相关。 特别强调:关于相关的种类,在考试中出题经常出现,大 家一方面要掌握不同种类的名称,另外,还要判断相关的类型。 (三)相关分析的主要内容。研究两个变量之间的密切程度, 将定性→定量,包括如下几个环节。 1.确定相关关系的存在,相关关系的形态和方向。 2.确定相关关系的数学表达式。将两个变量用一个近似的 方程来表示,这就是本章第二重点一一回归分析。 3.确定因变量估计值误差的程度。既然在(2)中提到,用 一个近似方程来定义两变量的关系,这就表明用方程确 定出来的数值与实际数值之间仍有一定的差距,只是一 个估计值而已,所以我们应该对方程值与实际值计算误 差,来检验方程的代表程度。 (四)相关图表 1.相关表的编制。 可以直观地判断现象之间大致呈何种关系形式。 (1)简单相关表:未分组的相关表,把因素标志(x) 按照从小到大的顺序并配合结果标志(因变量y) 4
4 2) 联系:相关关系是相关分析的研究对象, 函数关系是相关分析的工具 (二)相关的种类 1.按相关的程度分为完全相关和不完全相关,不相关 2.按相关的方向分为正相关和负相关 3.按相关的形式分为线性相关和非线性相关。 对应数值的图形近似一条直线 4.按影响因素的多少可分为单相关和复相关。 特别强调:关于相关的种类,在考试中出题经常出现,大 家一方面要掌握不同种类的名称,另外,还要判断相关的类型。 (三)相关分析的主要内容。研究两个变量之间的密切程度, 将定性 → 定量,包括如下几个环节。 1.确定相关关系的存在,相关关系的形态和方向。 2.确定相关关系的数学表达式。将两个变量用一个近似的 方程来表示,这就是本章第二重点——回归分析。 3.确定因变量估计值误差的程度。既然在(2)中提到,用 一个近似方程来定义两变量的关系,这就表明用方程确 定出来的数值与实际数值之间仍有一定的差距,只是一 个估计值而已,所以我们应该对方程值与实际值计算误 差,来检验方程的代表程度。 (四)相关图表 1.相关表的编制。 可以直观地判断现象之间大致呈何种关系形式。 (1) 简单相关表:未分组的相关表,把因素标志(x) 按照从小到大的顺序并配合结果标志(因变量 y)

一一对应而平行排列起来。如图: 2345.min-max 少53974.对应值 (2)分组相关表。 单变量分组相关表:对自变量进行分组,编制统计分布, 计算因变量的平均数 双变量分组相关表:对自变量和因变量都进行分组 2、相关图的编制。将(x,y)实际数值放于指教坐标系中去, 结合各有序实数所对应的点形成的大致图象来判断相关密 切程度、相关方向。 (五)相关系数 1.相关系数的基本公式 r= 表明度量x、y关系主要是通过两个变量的变异程度来说明的。 此公式中包括这几个方面: (1)62xy是协方差 x是x的标准差可是y的标准差 (②)62xy协方差对相关系数r的影响,决定: [r>0或<0(正、负) r数值的大小 2.相关系数的性质 (1)r取值范围:H≤1 -1≤r≤1
5 一一对应而平行排列起来。如图: ( 2 (2)分组相关表。 双变量分组相关表:对自变量和因变量都进行分组 计算因变量的平均数 单变量分组相关表:对自变量进行分组,编制统计分布, 2、 相关图的编制。将(x, y)实际数值放于指教坐标系中去, 结合各有序实数所对应的点形成的大致图象来判断相关密 切程度、相关方向。 (五)相关系数 1.相关系数的基本公式 x y xy r 2 = 表明度量 x、y 关系主要是通过两个变量的变异程度来说明的。 此公式中包括这几个方面: (1) xy 2 是协方差 x 是 x 的标准差 y 是 y 的标准差 (2) xy 2 协方差对相关系数 r 的影响,决定: 数值的大小 或 正、负) r r 0 r 0( 2.相关系数的性质 (1) r 取值范围: r 1 -1 r 1 X 1 2 3 4 5 .min——max y 5 3 9 7 4 .对应值