
第二节光的相速度和群速度 折射率是光在真空中和介质中传播速度的比值,=一。通常可以 通过测定光线方向的改变并应用折射定律,=s血来求它。但原则 sin i, 上也可以分别实测c和U来示它们的比值。对于水n*=1.33,用这 两种方法测得的结果是符合的,但对cS,用折射法测得=1.64,而 1885年迈克耳孙用实测光速求得的比值=1.75,其间差别很大,这 绝不是实验误差所造成的。瑞利找到了这种差别的原因,他对光速 概念的复杂性进行了说明,从而引出了相速度和群速度的概念。 按照波动理论,这种通常的光速测定法相当于测定由下列方程所 决定的波速的数值:E=Acos0t- 这里所代表的是单色乎面波的一定的位相向前移动的速度,因 为位相不变的条件为t-一=常数 dt ar 2 =0 d 所以这个速度称为位相速度。这速度的量值可用波长和频率来计 算
第二节 光的相速度和群速度 折射率是光在真空中和介质中传播速度的比值, 。通常可以 通过测定光线方向的改变并应用折射定律 来求它。但原则 上也可以分别实测c和 来示它们的比值。对于水n水=1.33,用这 两种方法测得的结果是符合的,但对cs2,用折射法测得n=1.64,而 1885年迈克耳孙用实测光速求得的比值n=1.75,其间差别很大,这 绝不是实验误差所造成的。瑞利找到了这种差别的原因,他对光速 概念的复杂性进行了说明,从而引出了相速度和群速度的概念。 按照波动理论,这种通常的光速测定法相当于测定由下列方程所 决定的波速的数值: 这里u所代表的是单色平面波的一定的位相向前移动的速度,因 为位相不变的条件为 常数 所以这个速度称为位相速度。这速度的量值可用波长和频率来计 算

E=Acos(ot -kr) 0= T、 都是不随和而改变的量。故位相不变的条件为 0t-=常数 odt kdr 0 d_0_2r.元=以 dtRT2π
、 都是不随t和r而改变的量。故位相不变的条件为 常数

上式表示的位相速度是严格的单色波(有单一的确定值)所特有 的一种速度,单色波以和的余弦函数表达,为常量。这种严格的 单色波的空间延续和时间延续都是无穷无尽的余弦波,但是这种波 仅是理想的极限情况,实际所遇到的永远是形式不同的脉动,这种 脉动仅在空间某一有限范围内,在一定的时间间隔内发生。任何脉 动可写成傅里叶级数或傅里叶积分。在无色散介质中所有这些组成 脉动的单色平面波都以同一相速度传播,那该脉动在传播过程中将 永远保持形状不变,整个脉动也永远以这一速度向前传播。但在有 色散的介质中,关于脉动的传播速度问题就变得比较复杂了。观察 这种脉动时,可以先认定上面某一特殊点,而把这一点在空间的传 播速度看作是代表整个脉动的传播速度。但是由于脉动形状的改变 所选定的这一特殊点在脉动范围内也将不断改变其位置,因而该点 的传播速度和任何一个作为组成部分的单色平面波的相速都将有所 不同。按照瑞利的说法,这脉动称为波群,因而脉动的传播速度称 为群速度,现在仅就一个简化的例子来讨论两种速度的关系
上式表示的位相速度是严格的单色波( 有单一的确定值)所特有 的一种速度,单色波以t和r的余弦函数表达, 为常量。这种严格的 单色波的空间延续和时间延续都是无穷无尽的余弦波,但是这种波 仅是理想的极限情况,实际所遇到的永远是形式不同的脉动,这种 脉动仅在空间某一有限范围内,在一定的时间间隔内发生。任何脉 动可写成傅里叶级数或傅里叶积分。在无色散介质中所有这些组成 脉动的单色平面波都以同一相速度传播,那该脉动在传播过程中将 永远保持形状不变,整个脉动也永远以这一速度向前传播。但在有 色散的介质中,关于脉动的传播速度问题就变得比较复杂了。观察 这种脉动时,可以先认定上面某一特殊点,而把这一点在空间的传 播速度看作是代表整个脉动的传播速度。但是由于脉动形状的改变, 所选定的这一特殊点在脉动范围内也将不断改变其位置,因而该点 的传播速度和任何一个作为组成部分的单色平面波的相速都将有所 不同。按照瑞利的说法,这脉动称为波群,因而脉动的传播速度称 为群速度,现在仅就一个简化的例子来讨论两种速度的关系

假设脉动由两个频率相近且振幅相等的单色简谐波叠加而成。 E Acos(@t-kr) E2=Acos(@,t-k2r) 0=0。+60 0=0-60 k1=k。+永k2=k。-永 E=E+E2=Acod@t-kr)+Acos@t-k,r) =2 4cost·6w-r.cos@,t-k,r) A cos@t-kor) A=2Acost.8o-r.&
假设脉动由两个频率相近且振幅相等的单色简谐波叠加而成
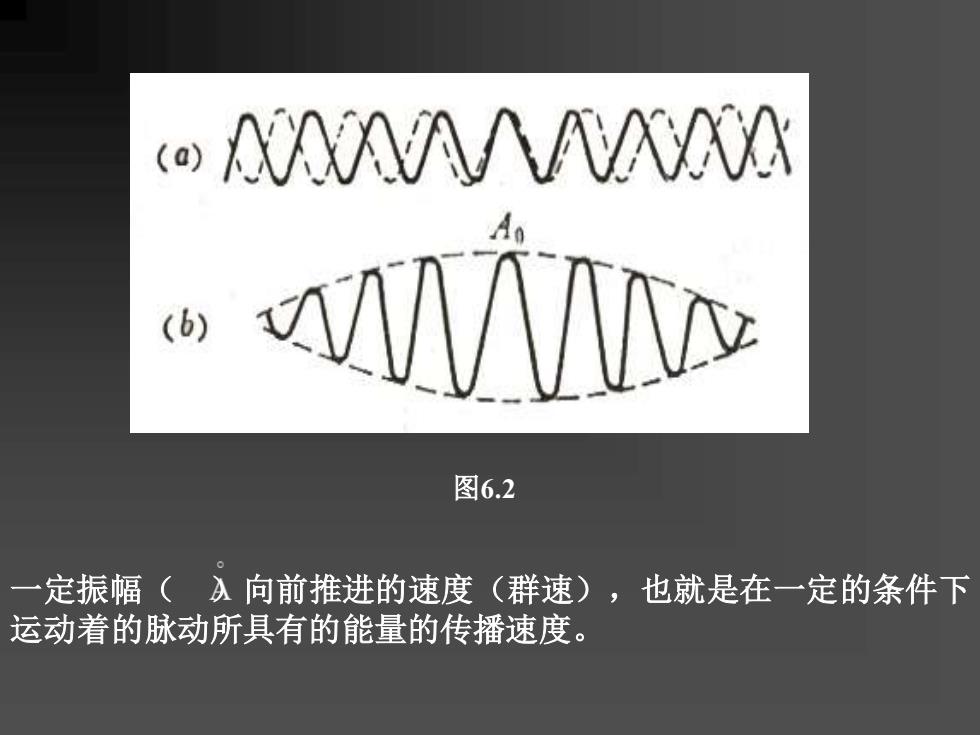
NMNAAKAO (b) 图6.2 一定振幅(入向前推进的速度(群速),也就是在一定的条件下 运动着的脉动所具有的能量的传播速度
一定振幅( )向前推进的速度(群速),也就是在一定的条件下 运动着的脉动所具有的能量的传播速度。 图6.2