上海交通大学：《大学物理》课程教学资源（课件讲稿）静电场与物质的相互作用、电介质

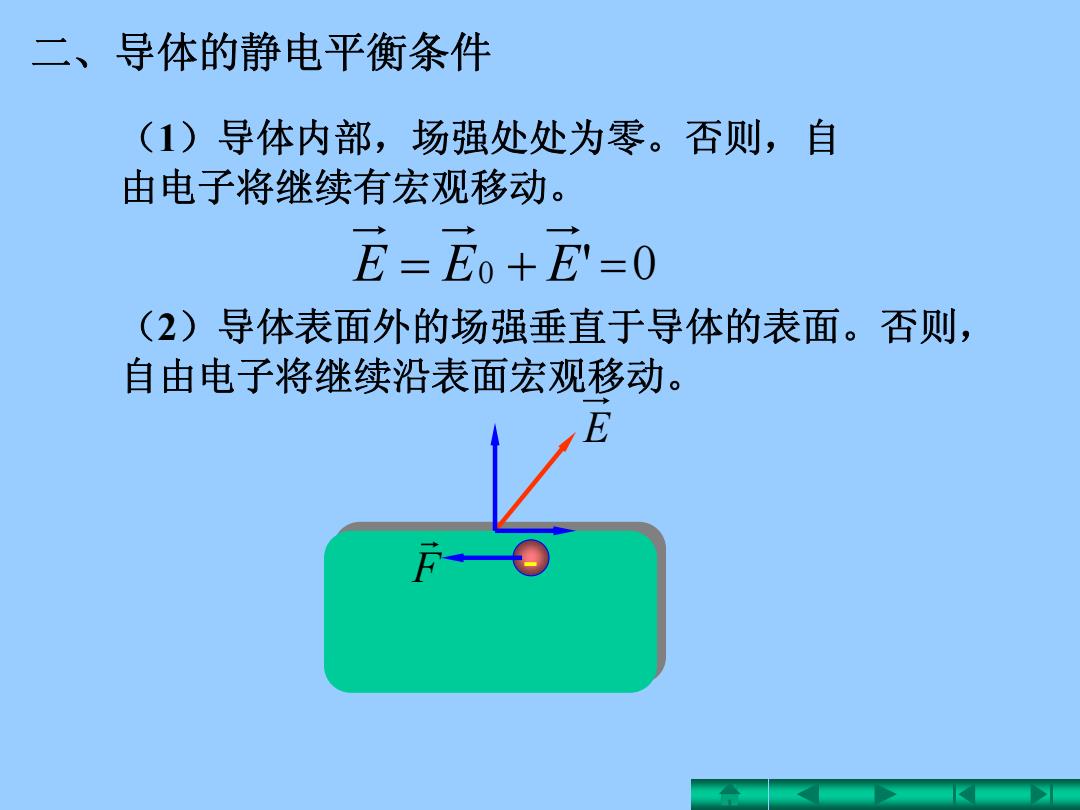
二、导体的静电平衡条件 (1)导体内部，场强处处为零。否则，自 由电子将继续有宏观移动。 E=E0+E=0 (2)导体表面外的场强垂直于导体的表面。否则， 自由电子将继续沿表面宏观移动

二、导体的静电平衡条件 （ 2）导体表面外的场强垂直于导体的表面。否则， 自由电子将继续沿表面宏观移动。 0  EEE '  0 （ 1）导体内部，场强处处为零。否则，自 由电子将继续有宏观移动。 E F - 

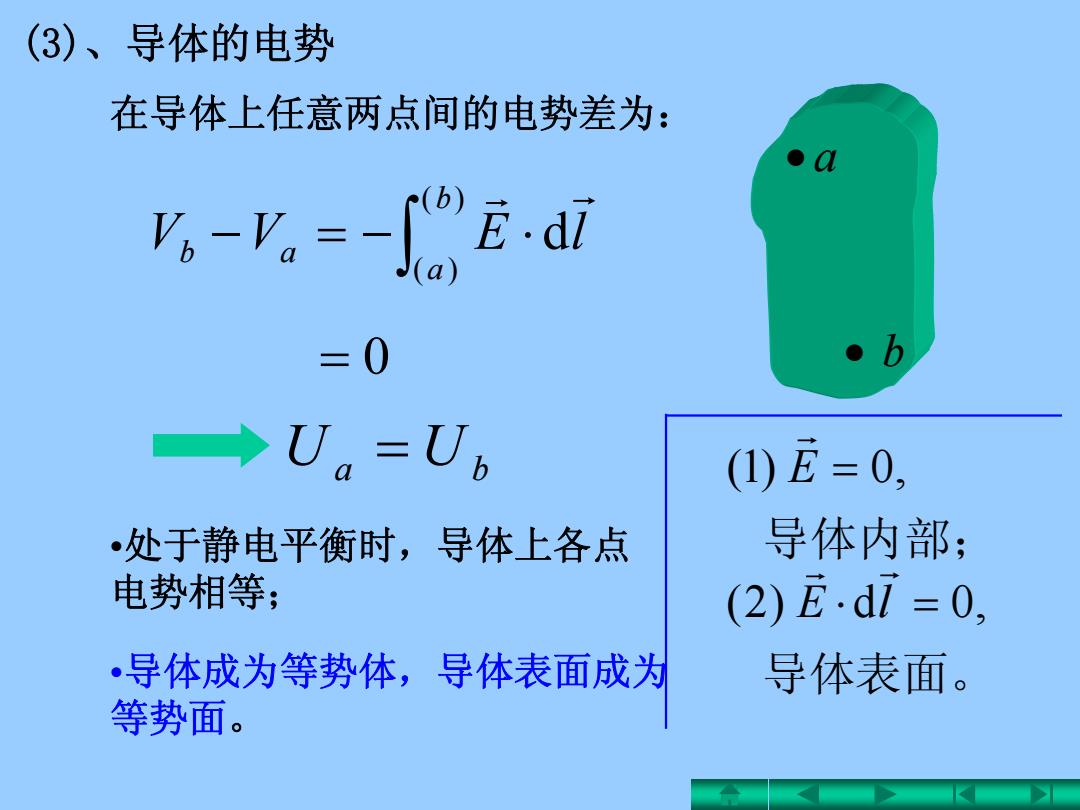
(3)、导体的电势 在导体上任意两点间的电势差为： -=-%6 =0 >U,=U6 (1)E=0, 处于静电平衡时，导体上各点 导体内部； 电势相等； (2)E·d1=0, 导体成为等势体，导体表面成为 导体表面。 等势面

 UU ba   )( )( d ba ab lEVV    0 •处于静电平衡时，导体上各点 电势相等； 在导体上任意两点间的电势差为：  a  b (3)、导体的电势 •导体成为等势体，导体表面成为 等势面。 导体内部； E  ,0 )1(  导体表面。 lE  ,0d )2(  

13.1.2、导体电荷的分布 1.电荷只分布在导体表面上，导体内部处处不带电 在导体内任取一高斯面S,由高斯定理： E.as=0 E内=0 →∑9=Jpr=0 S内 …高斯面为任意 >p=0(导体内部) 导体内部没有净电荷，电荷只能分布在导体表面

1. 电荷只分布在导体表面上，导体内部处处不带电  0d S SE   0d   Vq V S  内 在导体内任取一高斯面 S，由高斯定理： 高斯面为任意 E内  0 13.1.2、导体电荷的分布 导体内部没有净电荷，电荷只能分布在导体表面。 S + + + + + + + + + + + + + + + + + + + + E内  0   （导体内部） 0

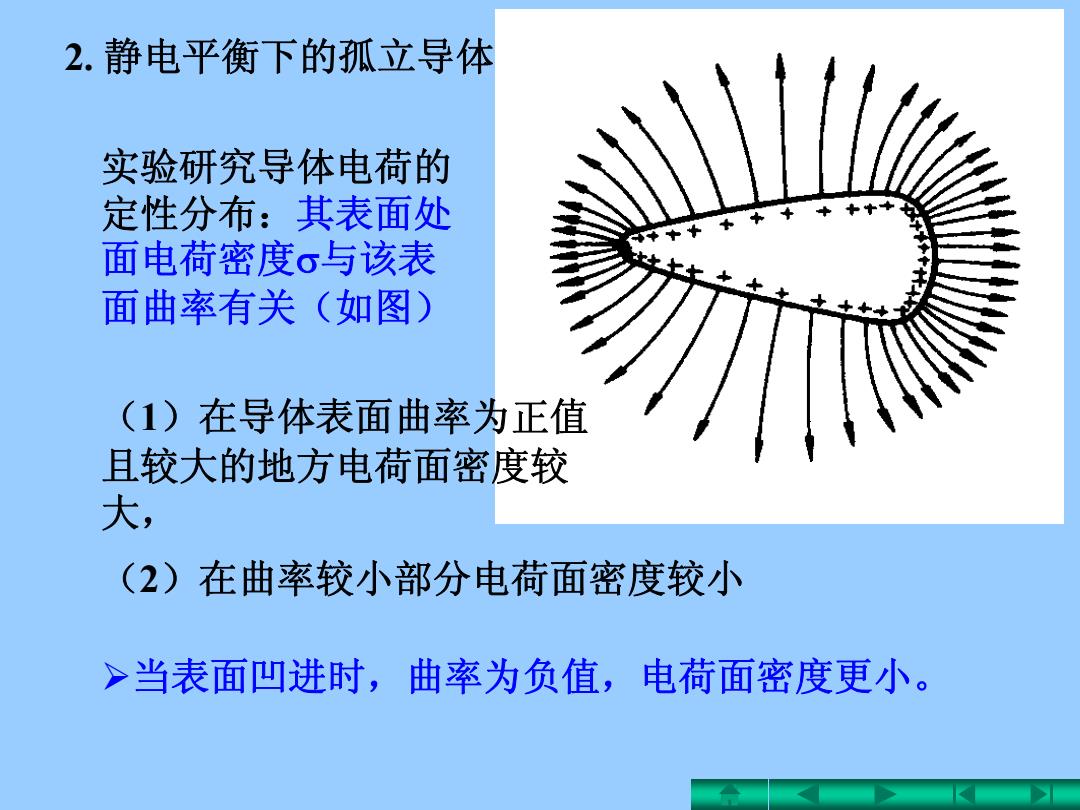
2.静电平衡下的孤立导体 实验研究导体电荷的 定性分布：其表面处 面电荷密度σ与该表 面曲率有关（如图） (1)在导体表面曲率为正值 且较大的地方电荷面密度较 大， (2)在曲率较小部分电荷面密度较小 >当表面凹进时，曲率为负值，电荷面密度更小

（1）在导体表面曲率为正值 且较大的地方电荷面密度较 大， 2. 静电平衡下的孤立导体 实验研究导体电荷的 定性分布：其表面处 面电荷密度与该表 面曲率有关（如图） （2）在曲率较小部分电荷面密度较小 当表面凹进时，曲率为负值，电荷面密度更小

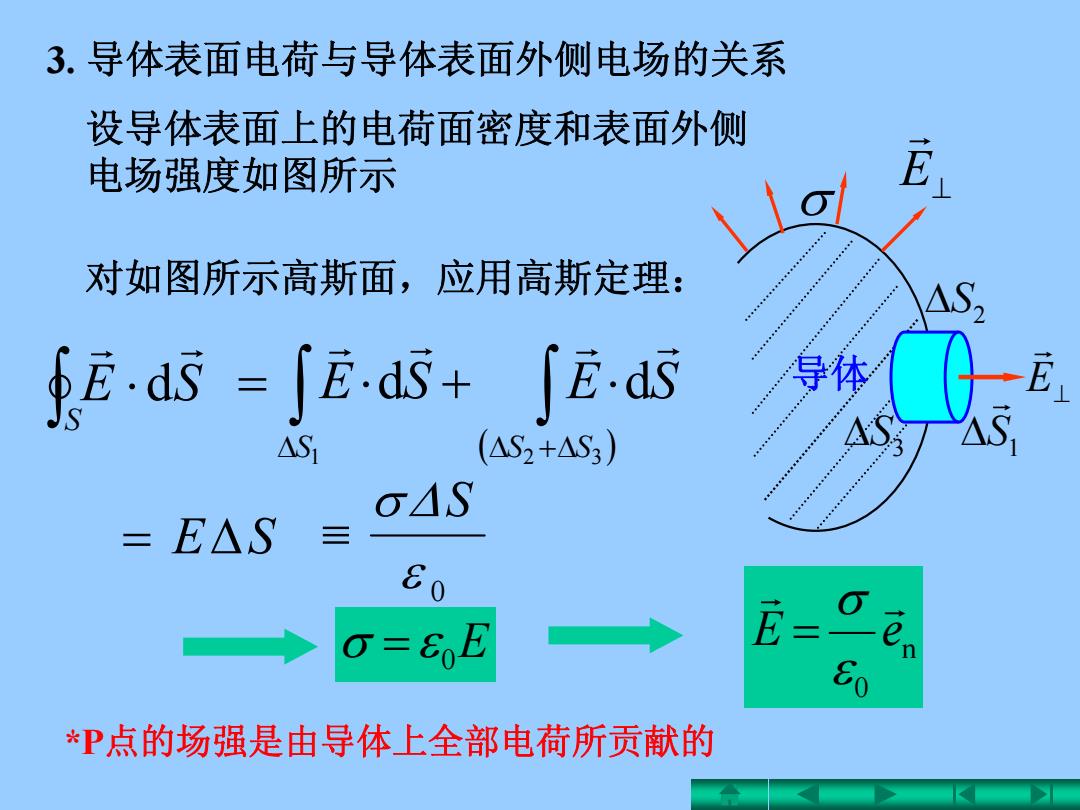
3.导体表面电荷与导体表面外侧电场的关系 设导体表面上的电荷面密度和表面外侧 电场强度如图所示 对如图所示高斯面，应用高斯定理： fEds=∫Eds+∫Eds 导体 △S1 (△S2+△S3) OAS =E△S 三 =6E E 0 *P点的场强是由导体上全部电荷所贡献的

 E  导体 3. 导体表面电荷与导体表面外侧电场的关系   S SE  d      1 32 d d S SS SESE     SE 0  S  设导体表面上的电荷面密度和表面外侧 电场强度如图所示 对如图所示高斯面，应用高斯定理： n 0 eE     E  0   S1   S2 S3 E  *P点的场强是由导体上全部电荷所贡献的